15) Теорема Штейнера

Теорема Штейнера : момент інерції тіла відносно довільної осі дорівнює сумі моменту інерції відносно осі, яка паралельна даній, і добутку маси тіла на квадрат відстані між осями:

16) Рівняння обертального руху ТТ

Основне рівняння динаміки обертального руху

За другим законом Ньютона можна сформулювати рівняння обертального руху, де зовнішнім силам, які діють на тіло, відповідають моменти сил, масі — момент інерції, а прискоренню — кутове прискорення.

При одновісному обертанні

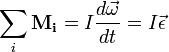
Тут M_i — моменти зовнішніх сил,   — кутова швидкість,   — кутове прискорення.

17) Моме́нт си́ли — векторна фізична величина, рівна векторному добутку радіус-вектора, проведеного від осі обертання до точки прикладення сили, на вектор цієї сили. Момент сили є мірою зусилля, направленого на обертання тіла.

Момент сили зазвичай позначається латинською літерою і вимірюється в системі СІ в Н*м

Момент сили , яка діє на матеріальну точку із радіус-вектором визначаєтся як

.

тобто є векторним добутком радіус-вектора на силу .

Момент сили - це вектор перпендикулярний, як до радіус-вектора точки, так і до сили, яка на цю точку діє. За абсолютною величиною момент сили дорівнює добутку сили на плече

,

де α - кут між напрямком сили й радіус-вектором точки.

Плече сили відносно точки (у механіці) - найкоротша відстань від даної точки до лінії дії сили, тобто довжина перпендикуляра, опущеного з цієї точки на лінію дії сили.

Новак

18.Правило важелів Архімеда

Правило важелів Архімеда: нерівні тягарі перебувають у рівновазі на важелі, якщо відстані центрів тягарів від точки опори важеля обернено пропорційні їх вагам.

19.Дисипативна енергія

Дисипація енергії - зменшення механічної енергіє системи в процесі руху.

Дисипати́вна систе́ма (або дисипати́вна структу́ра) — відкрита нелінійна система, яка є далекою від стану термодинамічної рівноваги. Така система є нерівноважною завдяки розсіянню енергії, одержуваної ззовні. Внаслідок самоорганізації у таких системах можуть виникати стійкі структури, які існують за умови постійної дисипації, тобто втрати системою енергії. З появою складної впорядкованої структури в системі зростає ентропія, яка компенсується негативним потоком ентропії зовні.

Дисипативна структура здійснює постійний обмін речовиною та енергією із середовищем, в котрому вона народилася, та є структурно стійкою у ньому. Класичним прикладом таких структур є комірки Бенара, винайдені у 1900 році. Ці комірки утворюються у воді, котру постійно підігрівають знизу, за рахунок конвекційних потоків. Як тільки система переходить в рівноважний стан, тобто підігрівання води припиняють, ці структури зникають.

1.Пружна деформація. Закон Гука. Модуль Юнга. Енергія деформованої пружини.

Пру́жна деформа́ція — деформація, що не викликає незворотних змін у структурі тіла.При пружній деформації тіло повертає собі попередні розміри й форму при знятті напруження.

Закон Гука

Сила, що виикає при деформації тіла, протидіє деформації.

Закон Гука встановлює лінійну залежність між деформацією й механічними напруженнями.

 — величина відносної деформації (відносне видовження);

E — модуль Юнга.

Модуль Юнга (модуль пружності) - фізична величина, що характеризує властивості матеріалу чинити опір розтягуванню / стисненню при пружній деформації. [ =[Па].

Енергія деформованої пружини

Для деформації тіла потрібно щоб сили, прикладені до нього виконукали роботу. Проте, деформоване тіло здатне виконувати роботу за рахунок енергії пружної деформації. Ця енергія дорівнює роботі пружних сил, якщо не відбувається зміна кінетичної енергії тіла. Для цього деформацію необхідно здійснювати повільно і зовнішні сили збільшувати так, аби зовнішні сили весь час зрівноважувалися з пружними силами.

2.Робота та потенціальна енергія. Зв'язок сили з потенціальною енергією МТ . Розрахунок роботи.

Робо́та – сила, яка діє на матеріальну точку і переміщає їїна деяку відстань. [A]=[Дж]

Потенціа́льна ене́ргія — частина механічної енергії, яка визначається взаємними положеннями матеріальних точок і характером сил взаємодії між ними.Позначається літерами або .

Потенціальною енергією матеріальної точки в полі консервативних сил називається функція , яка залежить тільки від положення точки:

Робота консервативних сил при переміщенні матеріальної точки дорівнює зменшенню потенціальної енергії точки.

Зв'язок сили з потенціальною енергією матер. точки:

Консервативна сила повязана з потенціальною енергією співвідношенням

. Саме при такому звязку між силою і потенціальною енергією в даній точці поля силове поле буде вважатися потенціальним

Потенціа́льна ене́ргія — частина механічної енергії системи, яка визначається взаємним положенням матеріальних точок і характером сил взаємодії між ними. Разом із кінетичною енергією, яка враховує не тільки положення тіл у просторі, а й рух, потенціальна енергія складає механічну енергію фізичної сиcтеми. Потенціальна енергія матеріальної точки визначається як робота з її переміщення із точки простору, для якої визначається потенціальна енергія ,у якусь задану точку, потенціальна енергія якої приймається за нуль. Потенціальна енергія визначається лише для поля консервативних сил.

Робо́та - фізична величина, яка визначає енергетичні затрати при переміщенні фізичного тіла, чи його деформації.

Розрахунок роботи

При малому переміщенні фізичного тіла   під дією сили   говорять, що над тілом здійснюється робота

,

де   - кут між напрямком сили й напрямком переміщення.

Згідно з цією формулою роботу здійснює тільки складова сили, яка паралельна переміщенню. Сила, яка перпендикулярна переміщеню, роботи не здійснює.

У випадку, коли тіло рухається по криволінійному контуру C, для знаходження роботи потрібно проінтегрувати наведений вище вираз вздовж контура:

Якщо сила   потенціальна, то робота залежить лише від різниці значень потенціалу в початоковій і кінцевій точках і не залежить від траєкторії, по якій тіло рухалося між цими двома точками.

У термодинаміці при зміні об'єму тіла на величину dV під дією тиску P над тілом виконується робота

.

3.Закон збереження енергії.

Закон збереження енергії : повна енергія системи, на яку діють консервативні сили, не змінюється з часом. Закон збереження енергії справедливий тільки для замкнених систем, тобто за умови відсутності зовнішніх полів чи взаємодій.

Сили взаємодії між тілами, для яких виконується закон збереження механічної енергії називаються консервативними силами.

4.Однорідне силове поле. Рух МТ в однорідному силовому полі.

Однорідним називається таке електричне поле, у всіх точках якого напруженість однакова.

На заряд, поміщений в нього, у всіх точках діють однакові сили. Силові лінії однорідного поля паралельні. Абсолютно однорідного електричного поля не існує.

Рух МТ в однорідному силовому полі.

В однорідному силовому полі на МТ діє сила Лоренца, яка завжди перпендикулярна до швидкості руху частинки. Це означає, що робота сили Лоренца завжди дорівнює нулю; отже, абсолютне значення швидкості руху частинки, а значить, і енергія частинки залишаються постійними при русі. Так як швидкість частинки u не змінюється, то величина сили Лоренца залишається постійною. Ця сила, будучи перпендикулярною,до напрямку руху, є доцентровою силою.