10) Третій закон Ньютона: закон дії та протидії

Сили, що виникають при взаємодії двох тіл, є рівними за модулем і протилежними за напрямом.

де  — сила, що діє на перше тіло з боку другого тіла, а  — навпаки, сила, що діє з боку першого тіла на друге тіло.

11) Робота та потенціальна енергія. Зв'язок сили з потенціальною енергією матер. Точки. Розрахунок роботи.

Робо́та – сила, яка діє на матеріальну точку і переміщає їїна деяку відстань. [A]=[Дж]

Потенціа́льна ене́ргія — частина механічної енергії, яка визначається взаємними положеннями матеріальних точок і характером сил взаємодії між ними.Позначається літерами або .

Потенціальною енергією матеріальної точки в полі консервативних сил називається функція , яка залежить тільки від положення точки:

Робота консервативних сил при переміщенні матеріальної точки дорівнює зменшенню потенціальної енергії точки.

Зв'язок сили з потенціальною енергією матер. точки:

Консервативна сила повязана з потенціальною енергією співвідношенням

. Саме при такому звязку між силою і потенціальною енергією в даній точці поля силове поле буде вважатися потенціальним

Розрахунок роботи:

При малому переміщенні фізичного тіла   під дією сили   говорять, що над тілом здійснюється робота

,

де   - кут між напрямком сили й напрямком переміщення.

Згідно з цією формулою роботу здійснює тільки складова сили, яка паралельна переміщенню. Сила, яка перпендикулярна переміщеню, роботи не здійснює.

У випадку, коли тіло рухається по криволінійному контуру C, для знаходження роботи потрібно проінтегрувати наведений вище вираз вздовж контура:

Якщо сила   потенціальна, то робота залежить лише від різниці значень потенціалу в початоковій і кінцевій точках і не залежить від траєкторії, по якій тіло рухалося між цими двома точками.

У термодинаміці при зміні об'єму тіла на величину dV під дією тиску P над тілом виконується робота

.

Закон збереження енергії в механіці:

Повна механічна енергія системи,на яку діють тільки консервативні сили, зберігається, тобто не змінюється з часом.

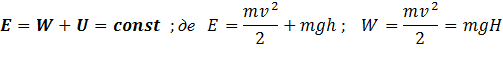
E - кінетична енергія, W – потенціальна енергія

Сили взаємодії між тілами, для яких виконується закон збереження механічної енергії називаються консервативними силами. Закон збереження механічної енергії не виконується для сил тертя, оскільки за наявності сил тертя відбувається перетворення механічної енергії в теплову.

Однорідне силове поле. Рух МТ в однорідному силовому полі.

Однорідне силове поле — силове поле, в будь-якій точці якого сила поля для даної матеріальної точки має одне і те ж значення.

14)Момент інерції твердого тіла. Мотенти інерції тіл найпростішої форми.

Момент інерції - скалярна фізична величина, міра інертності при обертальному русі навколо осі, подібно до того, як маса тіла є мірою його інертності в поступальному русі. Характеризується розподілом мас у тілі: дорівнює сумі добутків мас частинок тіла на квадрати їхніх відстаней від осі обертання.

Порожній тонкостінний циліндр масою m та радіусами циліндричних поверхонь відносно геометричної осі
Порожній тонкостінний циліндр масою m та радіусом оболонки відносно геометричної осі
Суцільний циліндр або диск радіуса r і маси m відносно геометричної осі
Куля радіуса r і маси m (вісь проходить через центр кулі)
Куб маси m та довжиною ребра а відносно осі, що проходить через центр куба перпендикулярно до його грані
Стержень маси m і завдовжки відносно осі, перпендикулярної до середини стержня
Стержень маси m і завдовжки відносно осі, перпендикулярної до кінця стержня

Момент інерції твердого тіла відносно якої-небудь осі залежить не тільки від маси, форми і розмірів тіла, але також від положення тіла по відношенню до цієї осі. Згідно теоремі Штейнера (теоремі Гюйгенса-Штейнера), момент інерції тіла J щодо довільної осі дорівнює сумі моменту інерції цього тіла J _c щодо осі, що проходить через центр мас тіла паралельно розглядається осі, і твори маси тіла m на квадрат відстані d між осями:

Якщо - Момент інерції тіла відносно осі, що проходить через центр мас тіла, то момент інерції щодо паралельної осі, розташованої на відстані від неї, дорівнює

,

де - Повна маса тіла.

Наприклад, момент інерції стрижня відносно осі, що проходить через його кінець, дорівнює: