2.2. Уравнение движения электропривода

Наиболее удобным методом составления уравнений движения механизмов является метод уравнений Лагранжа второго рода. Сложность уравнения движения будет зависеть от того, какую расчетную схему механической части привода мы выбрали. В большинстве практических случаев выбирают одномассовую, расчетную схему, сводя всю систему электродвигатель-рабочая машина (ЭД-РМ) к жесткому приведенному механическому звену.

Движение одномассовой системы описывается уравнением

, (2.10)

где – электромагнитный момент двигателя;

– момент сопротивления рабочей машины;

– момент инерции, приведённый к валу двигателя

.

При , что часто имеет место, уравнение движения имеет вид

.

Структурная схема соответствующая этому уравнению, будет выглядеть так: (рис. 2.3).

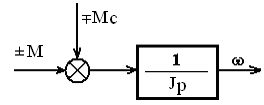
Рис. 2.3. Структурная схема привода

При работе ЭДУ в двигательном режиме М>0, а при работе в генераторном М<0. Если момент М_с является моментом сопротивления, перед ним ставится отрицательный знак, а если движущим – положительный. Для наиболее характерного режима работы ЭП, когда двигатель создает движущий момент, а ИО – тормозящий, уравнение движения выглядит так:

. (2.11)

Одномассовая система (жесткое приведённое звено) является интегрирующим звеном. В том случае, когда в кинематической цепи ЭП содержатся нелинейные связи, параметры которых зависят от положения отдельных звеньев механизма (пары кривошип – шатун, кулисный механизм и так далее) движение одномассовой системы описывается нелинейным дифференциальным уравнением с переменными коэффициентами. Входящие в это уравнение моменты в общем случае могут быть функциями нескольких переменных (времени, скорости, угла поворота).

Как следует из структурной схемы, момент двигателя представляет собой управляющее воздействие, а момент сопротивления - возмущающее воздействие.

2.3. Установившееся движение электропривода

Установившееся движение ЭП обусловлено равенством моментов двигателя и рабочей машины , в этом случае динамический момент будет равен нулю . Для исследования статического режима часто используют механические характеристики. Механические характеристики представляют зависимость сил или моментов от скорости движения.

Механические характеристики рабочей машины обычно изображают в виде зависимости (рис. 2.4). Каждая механическая система имеет свои характеристики. Но условно их можно разделить на четыре большие группы, которые объединяют большую часть применяемых на практике механизмов [13; 14].

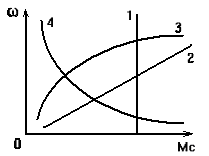
Рис. 2.4. Механические характеристики рабочей машины

1 группа механизмов – момент сопротивления которых не зависит от скорости (кривая 1), например: лебедки, конвейеры с постоянной массой перемещаемого груза, механизмы подач некоторых металлорежущих станков.

2 группа механизмов – момент сопротивления которых зависит линейно от скорости (кривая 2), например: генератор постоянного тока независимого возбуждения при работе на постоянный резистор.

3 группа механизмов – имеет нелинейно-возрастающую (вентиляторную) характеристику, момент сопротивления пропорционален квадрату скорости (кривая 3), например: вентиляторы, компрессоры, центробежные насосы и другие центробежные машины.

4 группа механизмов – имеет нелинейно-спадающую характеристику, момент сопротивления изменяется обратно пропорционально скорости, но не линейно. Обычно у этих механизмов мощность потребления остается постоянной (кривая 4), например, некоторые металлорежущие станки.

Механические характеристики двигателей изображают в виде зависимости . Для большинства двигателей эта зависимость является убывающей функцией момента. Степень изменения скорости с изменением момента и характер изменения для различных двигателей различен. В зависимости от вида механической характеристики ЭД делят на четыре основные группы (рис. 2.5):

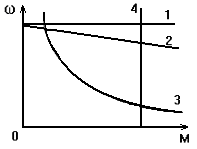
Рис. 2.5. Механические характеристики электродвигателей

1 группа двигателей – синхронные двигатели, скорость не изменяется при изменении момента (кривая 1). Характеристика абсолютно жесткая .

2 группа двигателей – у этих двигателей скорость несколько снижается при увеличении момента (кривая 2). Характеристика жесткая. Такой характеристикой обладают двигатели постоянного тока с независимым и параллельным возбуждением и асинхронные двигатели на рабочем участке характеристики.

3 группа двигателей – скорость значительно изменяется с увеличением момента (кривая 3). Характеристика мягкая. Такой характеристикой обладают двигатели постоянного тока с последовательным возбуждением.

4 группа двигателей – характеристика абсолютно мягкая . Такой характеристикой обладают двигатели постоянного тока с независимым возбуждением при их питании от источника тока либо в замкнутой системе при стабилизации тока якоря.

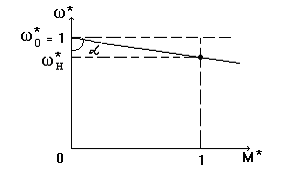
Рис. 2.6. Механическая характеристика

Для ЭД широко используют понятие жесткости механической характеристики:

- для линейной характеристики, (2.12)

- для нелинейной характеристики. (2.13)

Обычно механические характеристики двигателей имеют отрицательную жесткость. Понятие жесткости используют и для оценки механической характеристики РМ.

Для сопоставления различных двигателей используют понятие относительной жесткости. Если представить ω и М в относительных единицах (рис. 2.6), то получим

, , - для ДПТ последовательного возбуждения.

Тогда ,

- относительная жесткость. (2.14)

Если относительная жесткость механической характеристики больше 40, то характеристика абсолютно жесткая, если - жесткая, - мягкая.

Установившийся режим работы ЭП характеризуется равенством скоростей и моментов Д и РМ. Изображая характеристики двигателя (кривая 1, рис. 2.7) и рабочей машины (кривая 2), в первом квадранте найдем точку их пересечения.

- точка пересечения характеристик соответствует установившемуся режиму системы. Под воздействием возмущающих факторов система может отклониться от установившегося режима, но если она статически устойчива, то после снятия возмущения она вновь вернется в прежнее состояние.

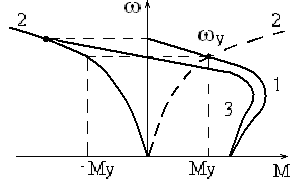
Рис. 2.7. Механические характеристики:

1-двигателя; 2- рабочей машины; 3- суммарная

Для того чтобы обеспечить статическую устойчивость, необходимо, чтобы при увеличении угловой скорости двигателя его момент оказался меньше момента сопротивления, а при уменьшении скорости больше момента сопротивления, тогда система будет сама возвращаться в положение равновесия. Понятие устойчивости обычно записывают через жесткость.

условие должно выполняться в точке устойчивости и тогда система будет статически устойчивой (Критерий статической устойчивости),

где - жесткость механической характеристики двигателя;

- жесткость механической характеристики рабочей машины.

В тех случаях, когда устойчивость системы ЭД-РМ оценить сложно, строят суммарную характеристику ЭД и РМ (кривая 3, рис. 2.7). Если совместная механическая характеристика имеет отрицательную жесткость, то система устойчива.