2. Механика электропривода

Электропривод представляет собой электромеханическую систему, состоящую из электрической и механической части. В этой главе мы рассмотрим механическую часть ЭП.

2.1. Расчетная схема механической части электропривода

В общем случае механическая часть ЭП включает в себя механическую часть электромеханического преобразователя (ротор или якорь электродвигателя), преобразователь механической энергии (редуктор или механическую передачу) и исполнительный орган рабочей машины (ИО РМ). Поскольку наша задача - это приведение в движение ИО РМ, основополагающими для выбора и расчета ЭП являются характеристики рабочей машины и особенности механической части ЭП [5; 9].

В общем случае механическая часть ЭП представляет собой сложную механическую систему, состоящую из нескольких вращающихся и поступательно движущихся с различными скоростями звеньев, имеющими различные массы и моменты инерции, соединенные упругими связями (малой или конечной жесткости). При этом в кинематических передачах часто имеют место зазоры.

На эту сложную механическую систему действуют различные по направлению и величине внешние моменты и силы, которые, в свою очередь, часто зависят от времени, угла поворота механизма, скорости движения и других факторов. Поскольку эта механическая система является неотъемлемой частью ЭП, необходимо знать её характеристики и иметь достаточно точное для инженерных расчетов математическое описание. Механическая часть ЭП описывается в общем случае системой нелинейных дифференциальных уравнений в частных производных с переменными коэффициентами. Для описания механической части ЭП наиболее удобным является использование уравнений Лагранжа второго рода.

Учитывая, что движение механической системы определяется наибольшими массами, наименьшими жесткостями и наибольшими зазорами; очень часто сложную механическую систему можно свести к двух-трех- массовой модели, которая может быть использована при расчете систем ЭП. (Это системы с гибкими валами, системы, подверженные резким динамическим нагрузкам, точные следящие системы).

В большинстве случаев механическая часть состоит из звеньев большой жесткости с жесткими связями, а зазоры мы стремимся свести к нулю, и тогда возникает возможность представить расчетную схему механической части как одномассовую систему, укрепленную на валу ЭД, при этом мы пренебрегаем упругостью механических связей и зазорами в передаче. Такая модель широко применяется для инженерных расчетов.

Для анализа движения механической части ЭП осуществляется переход от реальной кинематической схемы к расчетной, в которой массы и моменты инерции движущихся элементов их жесткости, а также силы и моменты, действующие на эти элементы, заменены эквивалентными величинами, приведенными к одной и той же скорости (чаще всего к скорости движения ЭД). Условием соответствия полученной расчетной схемы реальной механической части ЭП является выполнение закона сохранения энергии.

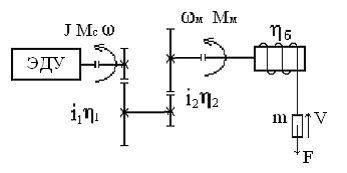
Рис. 2.1. Кинематическая схема подъемного устройства

Переход от реальной схемы (рис. 2.1) к расчетной (рис. 2.2) называют приведением. Все параметры механической части приводят к валу ЭД (в некоторых случаях к валу редуктора).

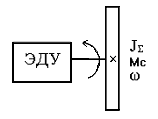
Рис. 2.2. Расчетная схема подъемного устройства

Приведение моментов инерции и масс осуществляется с помощью следующих известных из механики формул:

для вращательного движения , (2.1)

для поступательного движения, (2.2)

суммарный момент инерции системы, (2.3)

где – момент инерции двигателя, кг∙м²;

– момент инерции k-ого вращающегося элемента, кг∙м²;

– масса i-ого поступательно движущегося элемента, кг;

, – приведённые моменты инерции k и i элементов, кг∙м².

Моментом инерции тела относительно оси, проходящей через центр тяжести, называют сумму произведений массы каждой элементарной частицы тела на квадрат расстояния от соответствующей частицы до оси вращения

,

где R_j – радиус инерции

, (2.4)

i_k– передаточное число кинематической цепи между валом двигателя и k-ым элементом,

– угловые скорости вала двигателя и k-ого элемента, с^-1.

, (2.5)

где – радиус приведения поступательно движущегося i элемента к валу двигателя, м,

– скорость движения поступательно движущегося i элемента, м/с.

Радиусом инерции называют расстояние от оси вращения (проходящей через центр тяжести), на котором надо поместить массу рассматриваемого тела, сосредоточенную в одной точке, чтобы удовлетворить равенство

.

Приведение моментов и сил, действующих на элементы к валу двигателя, осуществляются следующим образом:

Первый вариант: передача энергии от двигателя к рабочей машине

- для вращательно движущихся элементов, (2.6)

- для поступательно движущихся элементов. (2.7)

Второй вариант: энергия передается от рабочей машины к двигателю

- для вращательно движущихся элементов, (2.8)

- для поступательно движущихся элементов. (2.9)

В этих выражениях:

– момент, действующий на k элемент, Н∙м;

– сила, действующая на i элемент, Н;

– приведённый момент (эквивалентный), Н∙м;

– КПД кинематической цепи между k и i элементом и валом двигателя.

С помощью приведенных расчётных схем осуществляется определение параметров, устойчивость и характер протекания переходных процессов в механической системе.

Динамику ЭП, как правило, определяет механическая часть привода как более инерционная. Для описания переходных режимов необходимо составить уравнение движения ЭП учитывающее все силы и моменты, действующие в переходных режимах [1; 9; 10; 11; 14].