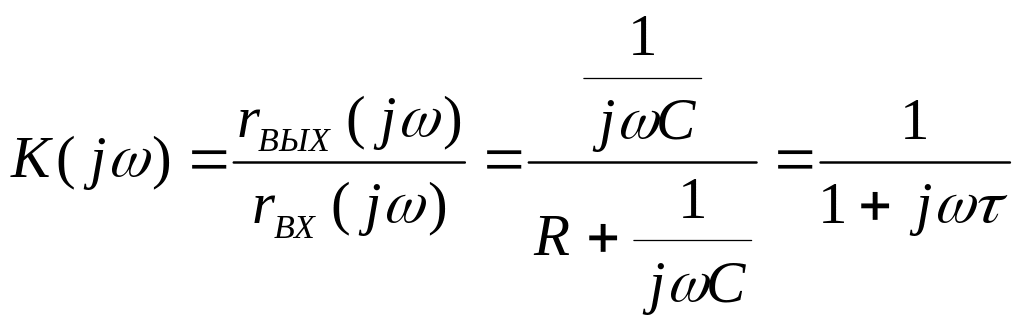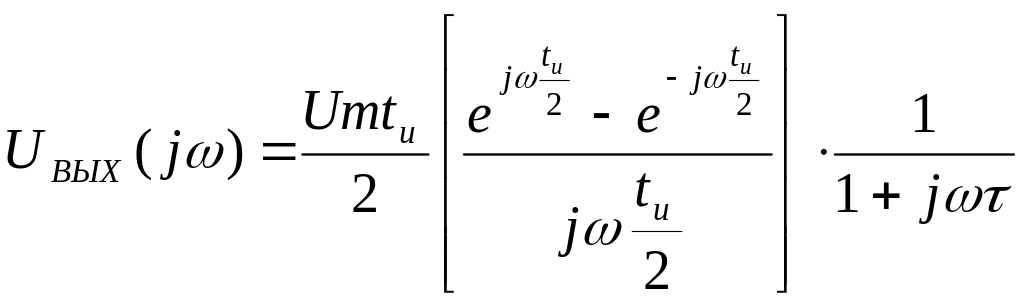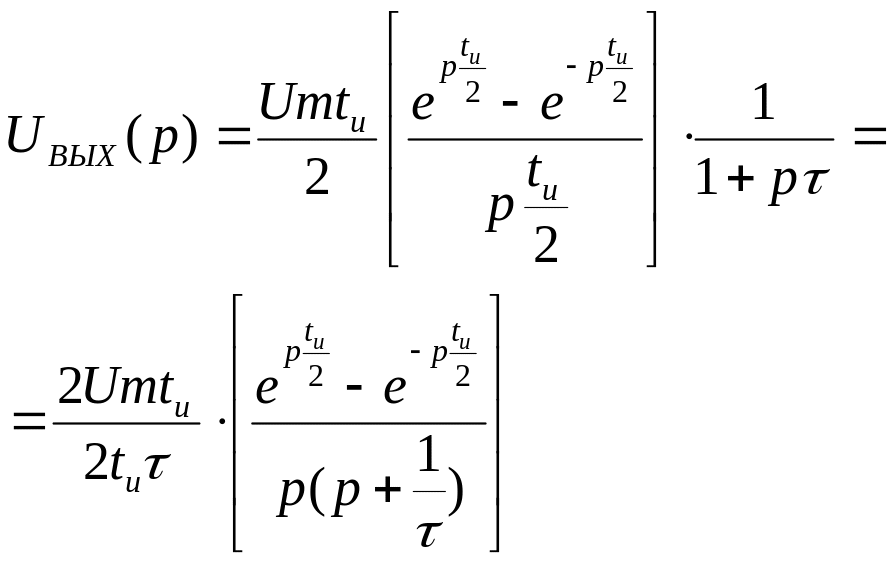18. Спектральний метод при проходженні неперіодичних сигналів через електричне коло. Поняття комплексної частоти. Основні співвідношення.

Спектральные методы, как уже известно, основаны на том, что исследуемый сигнал представляется в виде суммы неограниченно большого числа элементарных слагаемых, каждое из которых периодически изменяется во времени по закону .

Естественно обобщение этого принципа заключено в том, что вместо комплексных экспоненциальных сигналов счисто мнимыми показателями вводят в рассмотрение экспоненциальные сигналы вида , где комплексное число: , получившее название комплексной частоты.

Из двух таких комлексных сигналов можно составить вещественный сигнал, например, по следующему правилу:

(1)

где комплексно-сопряженная величина.

Действительно, при этом

(2)

В зависимости от выбора вещественной и мнимой частей комплексной частоты можно получить разнообразные вещественные сигналы. Так, если , но , получаются обычные гармонические колебания вида . Если же , то в зависимости от знака получаются либо наростающие, либо убывающие во времени экспоненциальные колебания. Более сложную форму такие сигналы приобретают, когда . Здесь множитель описывает огибающую, которая экспоненциально изменяется во времени. Некотрые типичные сигналы изображены на рисунке.

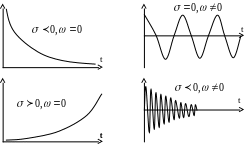
Понятие комплексной частоты оказывается весьма полезным прежде всего потому, что это дает возможность, не прибегая к обобщенным функциям, получать спектральные представления сигналов, математические модели которых неинтегрируемы. Существенно и другое соображение: экспоненциальные сигналы вида (2) служат «естественным» средством исследования колебаний в разнообразных линейных системах.

Следует обратить внимание на то, что истинная физическая частота служит мнимой частью комплексной частоты. Для вещественной части комплексной частоты специального термина не существует.

19. Спектральний метод при проходженні неперіодичних сигналів через електричне коло. Розрахунок реакції кола на проходження прямокутного відеоімпульсу через rc- коло.

Расчет реакции цепи на прохождение прямоугольного видеоимпульса через RC-цепь.

1. 

2. 

3. 

4. 

Приравниваем значение знаменателя к нулю для нахождения корней.

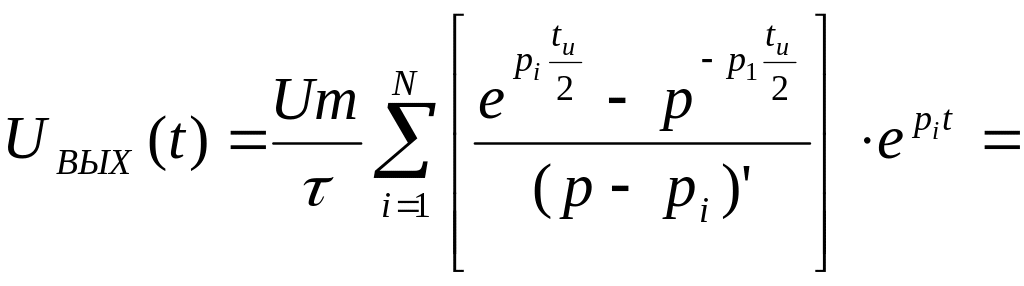
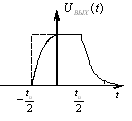
Хотя система и имеет корень с нулевым решением, однако для нашего случая явно видно, что обращается в ноль.

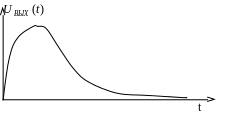
20. Спектральний метод при проходженні неперіодичних сигналів через електричне коло. Розрахунок реакції кола на проходження експоненціального відеоімпульсу через RC-коло.

    Расчет реакции цепи на прохождение экспоненциального видеоимпульса через RC-цепь.

1. 

2. 

3. 

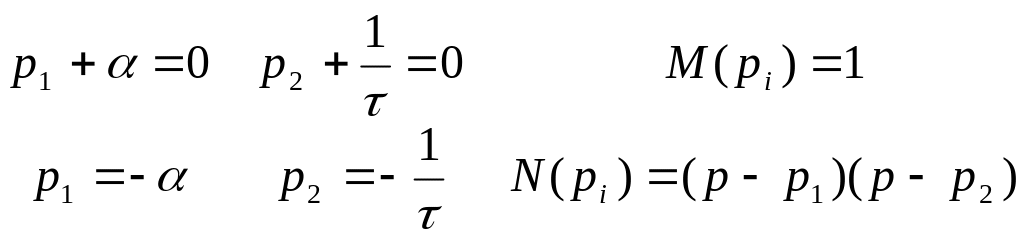
21. Фільтр нижніх частот Батерворта.

Т.к. идеальная характеристика коэффициента передачи физически не реализуема, то одиним из возможных видов аппроксимации данного идеального фильтра является вариант коэффициента передачи , предложенный Батервортом.

где -нормированная частота.

Фильтры, использующие такой коэффициент передачи, называются фильтрами с максимально плоской вершиной или фильтрами Батерворта.

Число -является порядком фильтра.

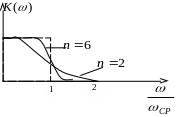
В полосе пропускания фильтра , где характеристика должна плавно уменьшаться и на частоте и на частоте среза ослабление фильтром должно составлять не зависимо от порядка системы. Однако видно, что чем больше порядок фильтра, тем точнее предложенный коэффициент перехода приближается к идеальной характеристике. Для дальнейшего синтеза фильтра необходимо перейти от коэффициента перехода к коэффициенту передачи системы в операторном виде.

Отсюда видно, что на комплексной плоскости функция , отвечающая ФНЧ с характеристикой Батерворта n-ого, имеет 2n полюсов, которые являются корнями уравнения.

Важная особенность: Если порядок фильтра нечетное число, то первый корень т.е. показатель степени при решении уравнения равен нулю, если же -четное, то первый корень начинается с .

Примечание.

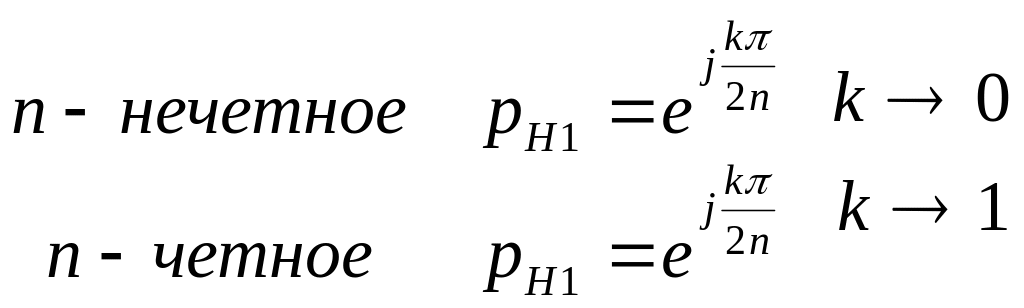
Рассчитаем аналоговый фильтр Батерворта для порядка фильтра . Тогда операторный коэффициент передачи будет.

Н айдем корни уравнения, стоящего в знаменателе и рассмотрим их на комплексной плоскости.

Из рассмотренной комплексной плоскости видно, что полюса располагаются симметрично на комплексной окружности . Тогда, казалось бы, коэффициенты передачи можно записать.

Однако данное решение не целесообразно и по той же теореме Винера-Хинчена физически нереализуема. Для физической реализации ФНЧ берутся полюса левой полуплоскости. Таким образом, решением уравнения будут .

Найдем операторный коэффициент передачи физически реализуемого ФНЧ Батерворта аналогового типа.

Тогда.

Перейдем от нормированной лаплассовской частоты к ненормируемой. При этом полюса.

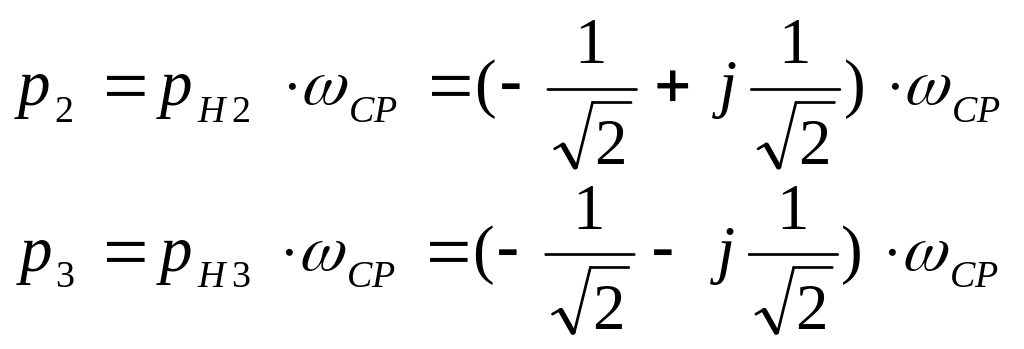
Тогда будет записана, как.

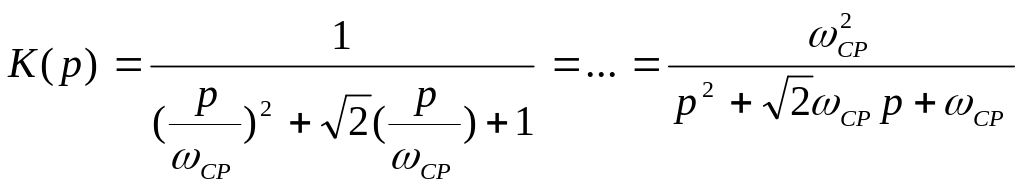
Операторный коэффициент передачи ФНЧ Батерворта второго порядка.

Построение АЧХ аналогового ФНЧ Батерворта второго порядка.

Для построения АЧХ перейдем от операторного коэффициента передачи к частотному .