15. Проходження сигналу через лінійні кола. Алгоритм розрахунку реакції кола для періодичних сигналів. Алгоритм расчета реакции цепи для периодических сигналов.

Д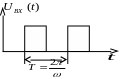 ля определения алгоритма расчета реакции цепи для периодических сигналов

1. Сначала необходимо разложить заданный сигнал в ряд Фурье.

(8)

2. Д ля заданной цепи находится частотный коэффициент передачи 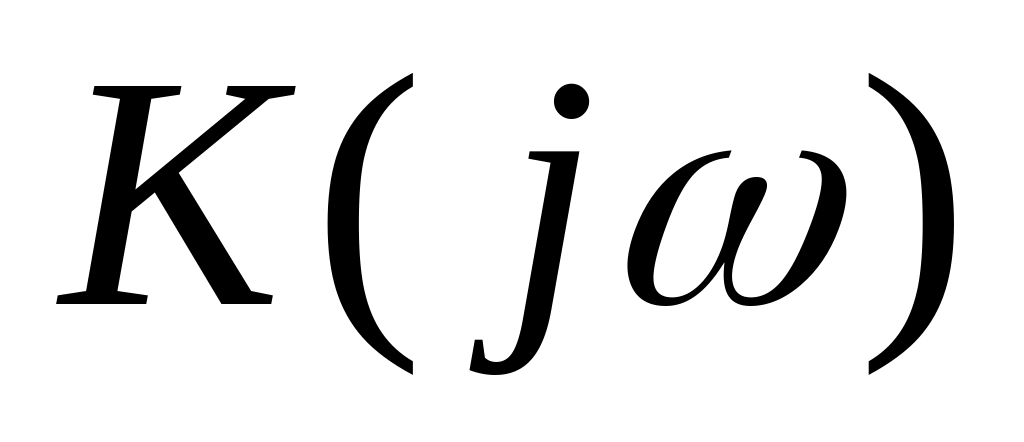. Данный частотный коэффициент передачи дискретизируется по оси частот с шагом дискретизации .

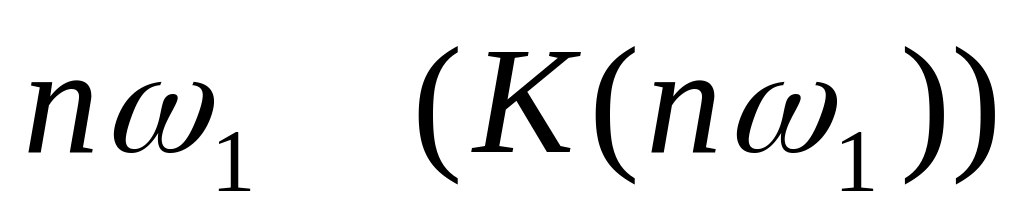3. Рассчитывается реакция цепи на сумму входных гармонических воздействий , представленных рядом Фурье. Выходная реакция определяется как сумма произведения амплитуды каждой из гармоник, умноженной на конкретной частоте.

(9)

(10)

(11)

16. Загальний підхід до спектрального методу при проходженні неперіодичних сигналів через електричне коло. Основна формула.

При расчете прохождения непрерывных сигналов спектральным методом используется прямое и обратное преобразования Фурье. Представление непрерывных функций в виде интеграла Фурье подразумевает суммирование бесконечного числа незатухающих и бесконечно близких друг к другу по частоте гармонических колебаний с бесконечно малыми амплитудами.

Следует отметить ограничения, накладываемые на частотный коэффициент передачи цепи.

Не каждый коэффициент передачи можно реализовать в физических системах. Для того чтоб был полностью реализуем необходимо выполнение двух условий.

1. На основании свойств преобразования Фурье 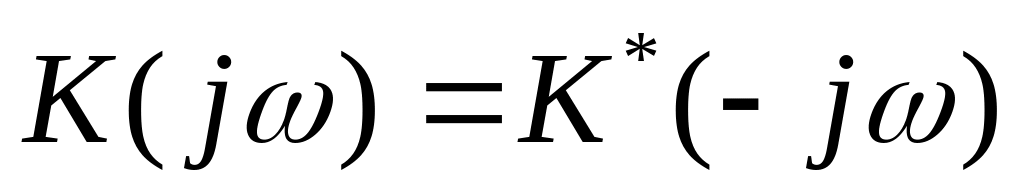. Т.е. модуль коэффициента передачи должен быть четной функцией, а аргумент коэффициента передачи- нечетной.

2. На основании доказательства теоремы Винера о физической реализуемости частотных характеристик важнейшим условием их реализуемости является условие:

Пример.

П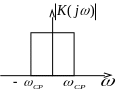 усть

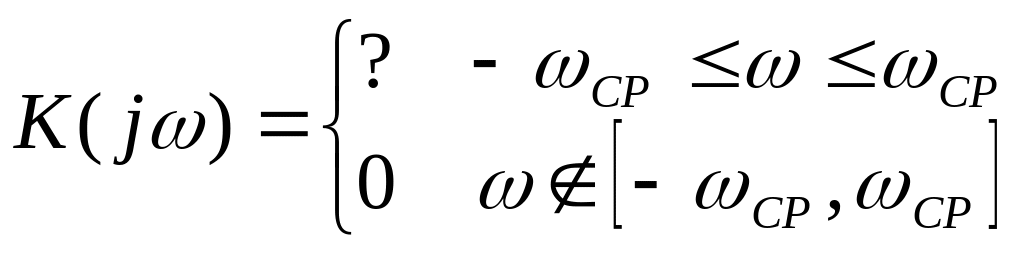
Попробуем найти

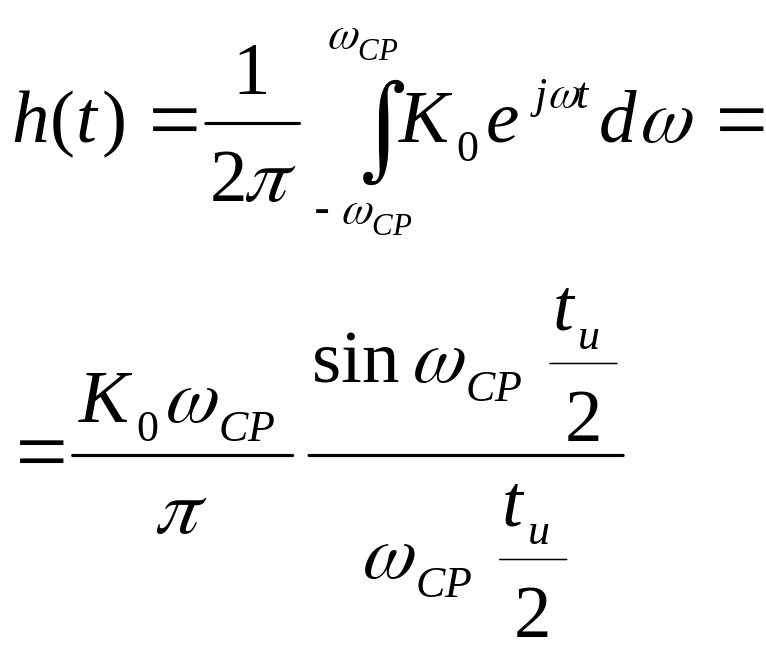
Рассмотрев ИХ видно, что она уходит в бесконечность, тогда не выполняются ограничения, накладываемые на импульсную характеристику, а значит предложенный коэффициент передачи нереализуем.

17. Розрахунок проходження неперіодичних сигналів через рт- кола. Основні положення теореми про розкладання.

1. Если есть 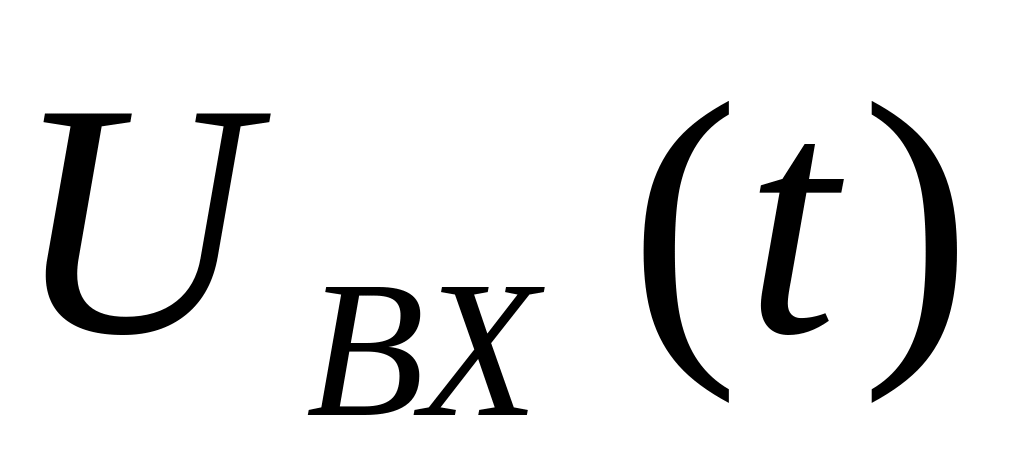, то необходимо найти его спектральную плотность.

2. Необходимо найти коэффициент передачи цепи .

3. Находим спектральную плотность сигнала на выходе.

2. находим реакцию цепи на выходе .

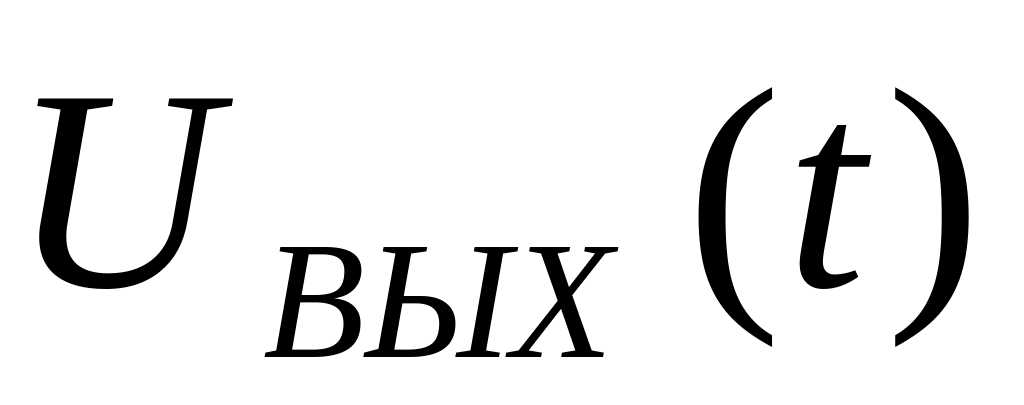Однако нахождение обратного преобразования Фурье и спектральной плотности выходного сигнала в большинстве случаев задача сложная т.к. будет иметь сложный вид. Поэтому.

1. Возможно применение теоремы о вычетах в частотной области.

2. а) переход к лаплассовским частотам, и взятие обратного преобразования Лапласа. Однако и данная задача может быть невыполнима, тогда.

б) переход к лаплассовским частотам и использование теоремы о разложениях.

2.При сложном нахождении оригинала путем решения ОПФ или обратным преобразованием Лапласа возможно использование теоремы о разложениях. Для использования теоремы о разложениях необходимо перейти из комплексной плоскости к лаплассовской частоте, при чем примем равной нулю.

1. 

3. 

4. 

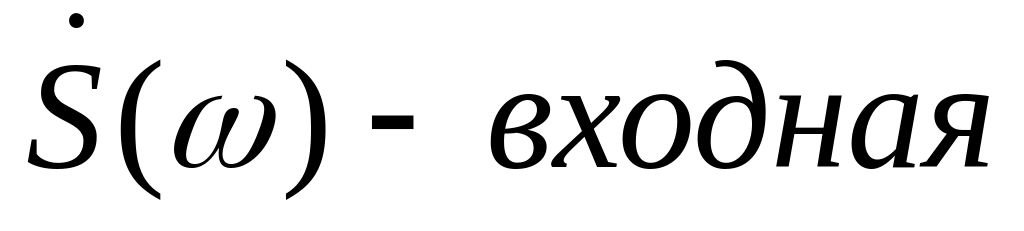
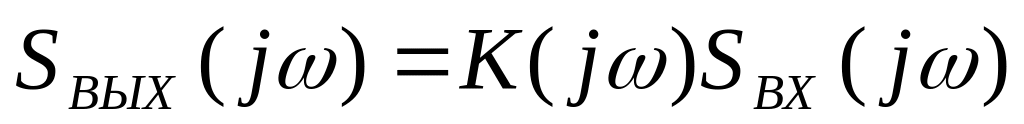
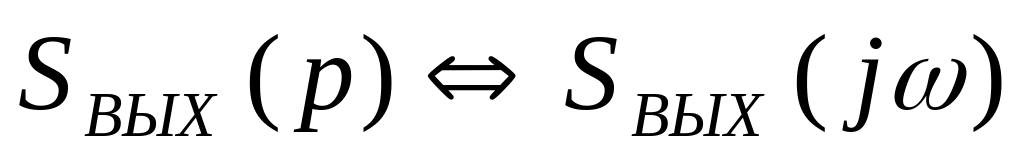
5. Теорема о вычетах

Запишем отношение изображений входного и выходного сигналов.

- передаточная функция цепи.

Для решения любой задачи операторный (частотный) коэффициент передачи нужно представить в каноническом виде.

Функция аналитическая на всей плоскости за исключением точек , являющихся корнями знаменателя коэффициента передачи системы. Функция не будет аналитична в точках, удовлетворяющих решению уравнения.

Корни , называются полюсами передаточной функции.

Рассмотрим частный случай, когда представляет собой отношение двух многочленов с указанными степенями и .

При чем будем считать, что степень числителя не превосходит степень знаменателя , кроме того, корни знаменателя должны быть простые и отрицательные.

Способ нахождения оригинала основывается на представлении функции в виде суммы элементарных дробей.

,где является вычетом функции в точках с полюсами .