74.Теорема о равнораспределении энергии по степеням свободы.

Среднее значение энергии одной молекулы . Если бы мы посчитали отдельно , то получили бы величину ровно в три раза меньшую, чем полная энергия. Такие же значения и для .

Таким образом, если вы молекула могла двигаться только вдоль оси , ее средняя энергия была бы . Говорят, что у молекулы, которая может совершать только одномерные движения – одна степень свободы: . Это значит. Что нужна только одна переменная, чтобы описать движение частицы. Для материальной точки таких переменных нужно 3: . Если же молекула может еще и вращаться, то число степеней свободы увеличивается. Средняя энергия, приходящаяся на одну степень свободы вращательного движения, а также на одну колебательную степень свободы (как потенциальной , так и кинетической) равна .

Теорема о равнораспределении энергии по степеням свободы: на все степени свободы статистической системы приходится одна и та же энергия . Это не относится к потенциальной энергии системы во внешних полях.

Средняя энергия одной молекулы , где число степеней свободы .

75.Расхождение теории теплоемкости идеального газа с экспериментом.

Н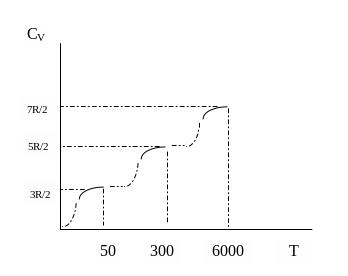 апример, для некоторого количества идеального газа: , его молярная теплоемкость

Для двух атомных молекул всего может быть 3-поступательных, 2-вращательных, 1-колебательная степени свободы. По расчетам для водорода (идеального газа) теплоемкость не зависит от температуры .

Зависимость теплоемкости молекулярного водорода от температуры, полученная в ходе экспериментов, дается на графике ( ).

Молекула водорода ведет себя при низкой температуре как точечная частица, у которой отсутствуют внутренние движения, при нормальной температуре – как жесткая гантель и наряду с поступательным движением также совершает вращательные движения, а при очень высокой температуре к этим движениям добавляются также колебательные движения атомов, входящих в молекулу. Объяснить эту зависимость классической теории не удалось.

Отличие экспериментальной кривой от теоретической прямой имеет квантовое объяснение. При низких температурах вращательные и колебательные степени свободы «выключены», т.е. они не возбуждаются. При температурах 116К могут возбуждаться вращательные степени свободы, а при температурах  4100К возбуждаются и колебательные степени свободы. Однако переход от одного режима движения к другому происходит не скачком при определенной температуре, а постепенно в некотором интервале температур. Это объясняется тем, что при определенной температуре возникает лишь возможность перехода молекул в другой режим движения, но эта возможность не реализуется сразу всеми молекулами, а лишь их частью.

76.Статистика Ферми-Дирака (подсчет числа микросостояний, функция распределения).

Подсчет числа состояний в статистике Ферми-Дирака. Различаем уровни энергии и различные состояния в пределах одной и той же энергии. Число различных состояний в пределах -го энергетического уровня , число этих состояний вообще различно для различных энергетических уровней. В этой модели частицы представляются шариками, которые нужно разместить по различным состояниям. Причем в модели Бозе-Эйнштейна в каждом состоянии может быть любое число шаров, а в модели Ферми-Дирака в одном состоянии может быть только один шар. Шары неразличимы между собой. Обозначим число шаров и проведем расчет числа возможных размещений шаров для модели Ферми-Дирака.

На каждом энергетическом уровне может находиться частиц, причем . Полное число частиц на всех уровнях равно . Прежде всего найдем число способов, сколькими не различимых между собой предметов могут быть размещены по местам. Ответ дается формулой, которая для рассматриваемых величин имеет вид: .

На каждом энергетическом уровне микросостояния независимы, и не играет роли, какие именно из частиц, находятся в каком именно состоянии, поэтому полное число состояний в совокупности всех энергетических уровней равно произведению числа микросостояний на каждом отдельном энергетическом уровне. - в произведении учитывает все возможные энергетические уровни.

- число микросостояний для модели Ферми-Дирака.

Удовлетворяя требование максимума числа микросостояний в равновесном состоянии, являющемся наиболее вероятным состоянием системы получаем формулу:

- распределения Ферми-Дирака, где - число частиц, приходящихся на одно квантовое состояние с энергией . Параметр . Параметр определяется нормировкой на полное число частиц, выражающей условие сохранения числа частиц: .

При очень малых значениях экспоненциальный член в знаменателе правой части должен быть значительно больше единицы. Поэтому единицей в знаменателе можно пренебречь и записать распределение в виде , где . Если теперь перейти к непрерывному спектру, то получится экспоненциальное распределение Максвелла-Больцмана.

Формулы статистики Ферми-Дирака переходят в формулы статистики Максвелла-Больцмана, когда среднее число частиц, приходящееся на одно квантовое состояние мало.