68.Экспериментальная проверка закона распределения.

Для экспериментальной проверки было проделано много опытов. Самый известный – опыт Штерна (1920). На оси двух коаксиальных цилиндров ( и ) расположена платиновая нить, покрытая слоем . Нить нагревали током, серебро испарялось, и его атомы хаотично вылетали по всем радиальным направлениям. При этом они имели и различные скорости движения. Воздух внутри цилиндров откачивался, чтобы столкновения молекул серебра с молекулами воздуха не искажали картину. Атомы серебра равномерно покрывали поверхность внешнего цилиндра, что указывало на равновероятность всех направлений их скорости. Затем во внутреннем цилиндре - узкая щель, диафрагмирующая пучок атомов по направлению (скорости любые по величине). Внешний цилиндр приводили во вращение ( ) об/мин.

В зависимости от скорости атомы попадают на разные участки поверхности вращающегося цилиндра, согласно формуле на участок АВ:

 .

Чем больше атомов осаждается на стенке, тем толще пленка. Измеряя толщину пленки, можем определить число атомов, обладающих скоростью, лежащей в некотором диапазоне, т.е. построить диаграмму, которая при сглаживании схожа с кривой распределения Максвелла .

69.Вывод основного уравнения молекулярно-кинетической теории идеального газа.

Применим распределение Максвелла для вывода основного уравнения кинетической теории газов. Наша задача установить путем статистического усреднения микрохарактеристик молекул системы, некоторые макрохарактеристики, описывающие газ в целом. Известно, что давление газа создается за счет ударов молекул газа о стенки сосуда. Примем, что удар является абсолютно упругим и молекулы бомбардируют стенки как материальные точки под разными углами и с различными скоростями.

По второму закону Ньютона: , .

Молекулы ударяются о стенку и отскакивают, меняя только -составляющую скорости. Подсчитаем изменение -составляющей импульса всех молекул за время . Надо подсчитать поток импульса молекул в положительном направлении оси , т.е. м², с, поток – число частиц пролетающих за единицу времени через единичную площадку. В стенку ударятся только те молекулы, которые движутся к ней, а не от нее, т.е. . За время до стенки долетают все молекулы в объеме , .

Вероятность частиц иметь такую скорость , тогда число частиц, имеющих такую скорость .

Импульс, передаваемый стенке сосуда

, вычислим отдельно внутренний интеграл и подставим в выражение

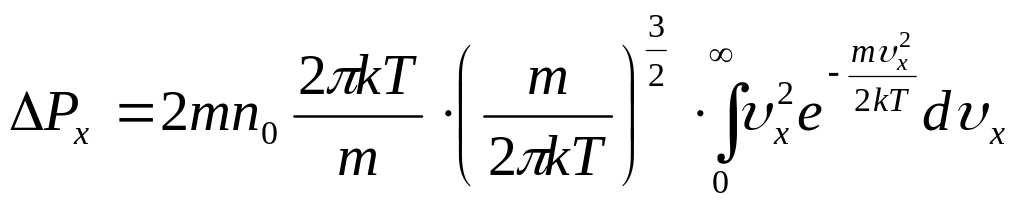, рассчитаем интеграл, сделав замену переменной,

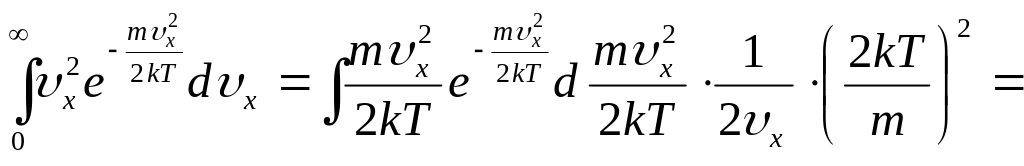
, , , отсюда , , , , , подставим полученное в интеграл:

. Таким образом давление на стенку

.

Аналогично для других стенок , с другой стороны , тогда , таким образом , - основное уравнение молекулярно-кинетической теории идеального газа.

Отсюда можно получить уравнение состояния идеального газа:

 - уравнение состояния идеального газа.

70.Вывод уравнения состояния. Закон Дальтона. Закон Авогадро.

, - основное уравнение молекулярно-кинетической теории идеального газа.

Отсюда можно получить уравнение состояния идеального газа:

 - уравнение состояния идеального газа.

Если имеется смесь газов, то - закон Дальтона (Давление смеси химически не взаимодействующих идеальных газов равно сумме парциальных давлений)

Закон Авогадро: В равных объемах газов (V) при одинаковых условиях (температуре Т и давлении Р) содержится одинаковое число молекул.

Первое следствие из закона Авогадро: один моль любого газа при одинаковых условиях занимает одинаковый объём.

В частности, при нормальных условиях, т.е. при 0° С (273К) и 101,3 кПа, объём 1 моля газа, равен 22,4 л/моль. Этот объём называют молярным объёмом газа Vm. Пересчитать эту величину на другие температуру и давление можно с помощью уравнения Менделеева-Клапейрона:

.

Второе следствие из закона Авогадро: молярная масса первого газа равна произведению молярной массы второго газа на относительную плотность первого газа по второму.

Используя распределение молекул по высоте Ж.Перрен экспериментально определил постоянную Авогадро. Он исследовал под микроскопом распределение броуновских частиц, т.е. считал под микроскопом число таких частиц на разных высотах в сосуде. Частицы были помещены в жидкость, плотность которой лишь на немного меньше плотности материала частиц, для того чтобы тяжелые частицы не «осели на дно», а распределились в достаточно большом слое по высоте.

, где - масса частицы, - масса вытесненной воды.

,  

.