
- •Оглавление
- •1.Предмет и задачи тд. Модели тд.
- •2.Модели тд. Объяснение агрегатных состояний вещества.
- •3.Методы тд.
- •4.Исходные понятия тд.
- •5.Постулаты термодинамики.
- •6.Начала тд.
- •7.Термическое и калорическое уравнения состояния. Термическое уравнение состояние идеального газа.
- •8.Внутренняя энергия идеального газа. Калорическое уравнение состояние идеального газа.
- •9.I начало термодинамики.
- •I начало тд обобщает закон сохранения энергии для тд процессов: количество теплоты, сообщаемое системе, идет на изменение ее внутренней энергии и совершение системой работы.
- •10.Теплоемкость.
- •11.Теплоемкость идеального газа.
- •12. 13.Теорема о равнораспределении энергии по степеням свободы. Число степеней свободы молекул. Число степеней свободы молекул. Выражение для внутренней энергии идеального газа.
- •14.Изохорический процесс: уравнение, график в pv, pt, vt координатах.
- •15.I начало термодинамики в изохорическом процессе.
- •16.Изобарический процесс: уравнение, график в pv, pt, vt координатах.
- •17. I начало термодинамики в изобарическом процессе.
- •18.Изотермический процесс: уравнение, график в pv, pt, vt координатах.
- •19.I начало термодинамики в изотермическом процессе.
- •20.Адиабатический процесс. Уравнение адиабаты. График адиабаты.
- •21.I начало термодинамики в адиабатическом процессе.
- •22.Политропный процесс. Уравнение политропы, показатель политропы, график политропы.
- •23.I начало термодинамики в политропном процессе.
- •24.Изопроцессы как предельные случаи политропного процесса.
- •25.Обратимые и циклические процессы.
- •26. Тепловые машины. Эффективность работы тепловой машины.
- •27.Холодильные машины. Эффективность работы холодильной машины.
- •28.29.Цикл Карно. К.П.Д. Цикла Карно. Идеальная тепловая машина Карно.
- •30. I Теорема Карно.
- •31.II теорема Карно. Реальные тепловые машины.
- •32.II начало термодинамики в формулировках Кельвина и Клаузиуса.
- •33.Тождество Клаузиуса, неравенство Клаузиуса.
- •34. Понятие энтропии. Свойства энтропии. Размерность.
- •35.Энтропия в обратимых и необратимых процессах.
- •36. Энтропия идеального газа.
- •37.III начало тд. Следствия III начала тд.
- •38.Энтальпия.
- •39.Свободная энергия идеального газа.
- •40.Метод тд потенциалов.
- •С 41 по 46 не разделила!смотреть тут(то что красным)!!!:
- •48.Условия равновесия и устойчивости системы в термостате при постоянном объеме.
- •49.Условия равновесия и устойчивости системы в термостате при постоянном внешнем давлении.
- •50.Условия равновесия и устойчивости системы при постоянных энтропии и давлении.
- •51. Условия равновесия и устойчивости системы при постоянных энтропии и объеме.
- •52.Условия равновесия и устойчивости системы с переменным числом частиц в термостате, при постоянных химическом потенциале и объеме.
- •53. Условия равновесия и устойчивости двухфазной однокомпонентной изолированной системы.
- •54.Принцип Ле Шателье-Брауна. Примеры проявления принципа Ле Шателье-Брауна.
- •55.Начала статистической физики: исходные понятия теории вероятности.
- •56.Начала статистической физики: макро- и микросостояния, статистический ансамбль, микроканонический ансамбль, постулат равновероятности.
- •57.Начала статистической физики: эргодическая гипотеза, статистический вес, статистическое толкование энтропии.
- •58.Начала статистической физики: флуктуации.
- •65.Характерные скорости распределения Максвелла: средняя квадратичная скорость.
- •66.Характерные скорости распределения Максвелла: наиболее вероятная скорость.
- •67. Подсчет числа молекул скорости, которых лежат в заданном диапазоне.
- •68.Экспериментальная проверка закона распределения.
- •69.Вывод основного уравнения молекулярно-кинетической теории идеального газа.
- •70.Вывод уравнения состояния. Закон Дальтона. Закон Авогадро.
- •71.72.( Не разделены!)Распределение Больцмана. (72)Барометрическая формула.
- •73.Экспериментальное определение постоянной Авогадро.
- •74.Теорема о равнораспределении энергии по степеням свободы.
- •75.Расхождение теории теплоемкости идеального газа с экспериментом.
- •76.Статистика Ферми-Дирака (подсчет числа микросостояний, функция распределения).
- •77.Статистика Бозе-Эйнштейна (подсчет числа микросостояний, функция распределения).
- •78.Длина свободного пробега.
- •79.Частота столкновений в единицу времени, понятие физического вакуума.
- •80.Явления переноса: теплопроводность.
- •81.Явления переноса: диффузия.
- •82.Явления переноса: вязкое трение.
- •83.Молекулярная теория явлений переноса: вывод уравнения переноса параметра .
- •84.Молекулярная теория явлений переноса: вывод уравнения коэффициента диффузии.
- •85.Молекулярная теория явлений переноса: вывод уравнения коэффициента теплопроводности.
- •86.Молекулярная теория явлений переноса: вывод уравнения коэффициента вязкости.
- •87.Силы и потенциальная энергия межмолекулярного взаимодействия.
- •88.Вывод уравнения Ван-дер-Ваальса.
- •89.Изотермы Ван-дер-Ваальса.
- •Часть 7—6 — отвечает газообразному состоянию;
- •Часть 2—1 — жидкому;
- •Часть 6—2, — горизонтальный участок, соответствующий равновесию жидкой и газообразной фаз вещества.
- •90.Фазовые переходы. Уравнения Клайперона-Клаузиуса.
- •91.Поверхностное натяжение в жидкостях.
- •92.Смачивание
- •93.Капиллярные явления. Формула Лапласса.
- •94.Строение твердых тел. Классификация элементарных ячеек.
- •95.Дефекты кристаллических решеток.
- •96.Температура. Температурные шкалы. Способы измерения.
58.Начала статистической физики: флуктуации.
Говорят, что величина флуктуирует, если ее значение колеблется около среднего. В статистической физике и термодинамике обычно имеются в виду флуктуации внутренних параметров в состоянии термодинамического равновесия.
Мерой флуктуаций является стандартное отклонение от среднего значения, которое определено равенством для дискретных величин:
![]()
При вычислении этой величины усреднение по времени можно заменить усреднением по ансамблю.
Стандартное отклонение растет медленнее, чем общее число частиц в системе, в то время как среднее растет пропорционально числу частиц в системе. Следовательно, относительное стандартное отклонение убывает сростом числа частиц в системе.
Расчет относительной величины флуктуации с помощью распределения Пуассона дает величину:
![]() .
.
Отметим, что относительная роль флуктуаций возрастает с уменьшением области, в которой эти флуктуации рассматриваются. Если область стремится к величине объема системы, то число частиц в этой области стремится к числу частиц системы.
Так как флуктуации
уменьшаются как
![]() ,
следовательно, с ростом числа частиц в
макросистемах флуктуации становятся
ничтожно малыми.
,
следовательно, с ростом числа частиц в
макросистемах флуктуации становятся
ничтожно малыми.
Поэтому поведение системы большого числа частиц можно описывать с помощью средних величин, характеризующих систему.
С 59 ПО 63 НЕ РАЗДЕЛИЛА ИЛИ НЕ НАШЛА!
59.Классическая статистика Максвелла-Больцмана: подсчет числа состояний.
60.Классическая статистика Максвелла-Больцмана: вывод функции распределения Больцмана (дискретное распределение).
61.Распределение Максвелла-Больцмана.
62.Распределение
Максвелла по проекциям скоростей
(определение константы
![]() из условия нормировки).
из условия нормировки).
63.Распределение Максвелла по абсолютному значению скорости.
64.Характерные скорости распределения Максвелла: средняя арифметическая скорость.
Средняя арифметическая скорость:
 выделим для замены
переменной
выделим для замены
переменной
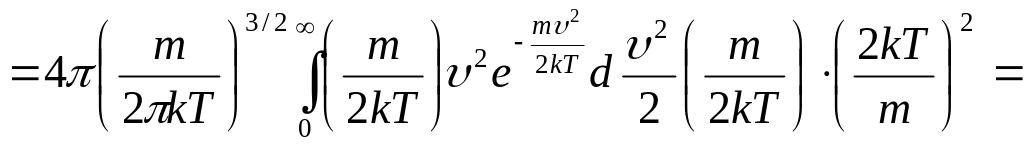
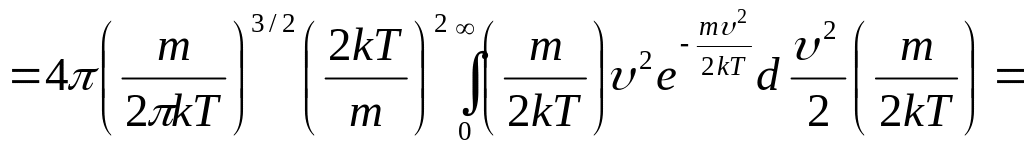 сделаем замену
переменной
сделаем замену
переменной
и учтем, значение
табличного интеграла:
![]() ,
,
![]() ,
получим после сокращения констант:
,
получим после сокращения констант:
![]() ,
где
,
где
![]() - постоянная Больцмана,
- постоянная Больцмана,
![]() - масса молекулы, преобразуем, умножив
числитель и знаменатель дроби на число
Авогадро:
- масса молекулы, преобразуем, умножив
числитель и знаменатель дроби на число
Авогадро:
![]() ,
где
- молярная масса компоненты системы.
,
где
- молярная масса компоненты системы.
Результат:
![]() - средняя арифметическая скорость
движения молекул идеального газа.
- средняя арифметическая скорость
движения молекул идеального газа.
65.Характерные скорости распределения Максвелла: средняя квадратичная скорость.
Средняя квадратичная скорость:
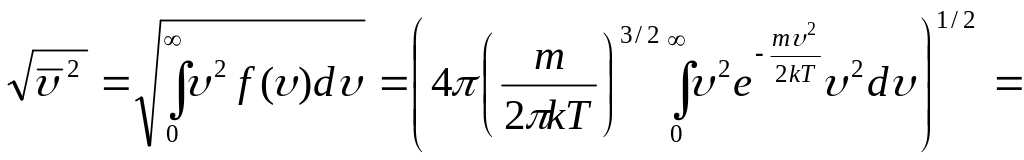 ,
,
сделаем замену переменной:
![]() ,
тогда
,
тогда
![]() ,
,
![]() ,
отсюда
,
отсюда
![]() ,
,
![]() ,
разделим переменные и найдем связь
между
,
разделим переменные и найдем связь
между
![]() и
и
![]() ,
подставим полученное значение в
дифференциал:
,
подставим полученное значение в
дифференциал:
![]() ,
, ![]() .
.
Подставим все в интеграл:
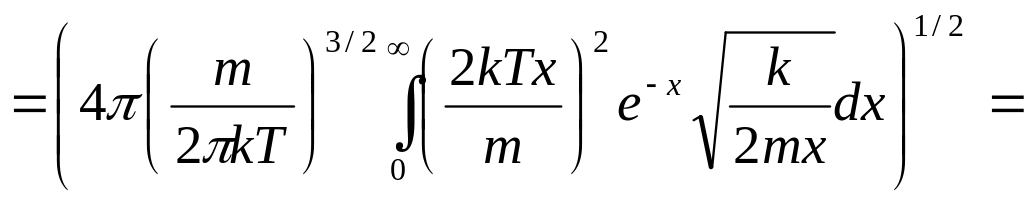 преобразуем,
преобразуем,
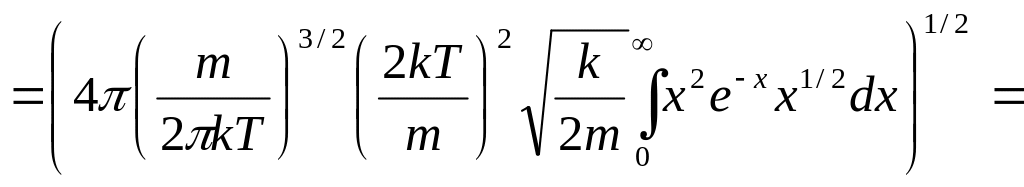
![]() ,
учтем значение табличного интеграла:
,
учтем значение табличного интеграла:
![]()
![]() ,
таким образом
,
таким образом
![]() - средняя
квадратичная скорость.
- средняя
квадратичная скорость.
66.Характерные скорости распределения Максвелла: наиболее вероятная скорость.
Наиболее вероятная скорость:
Наиболее вероятная скорость – это скорость, соответствующая максимуму кривой распределения молекул по скоростям, т.е. должно выполнятся условие:
![]()

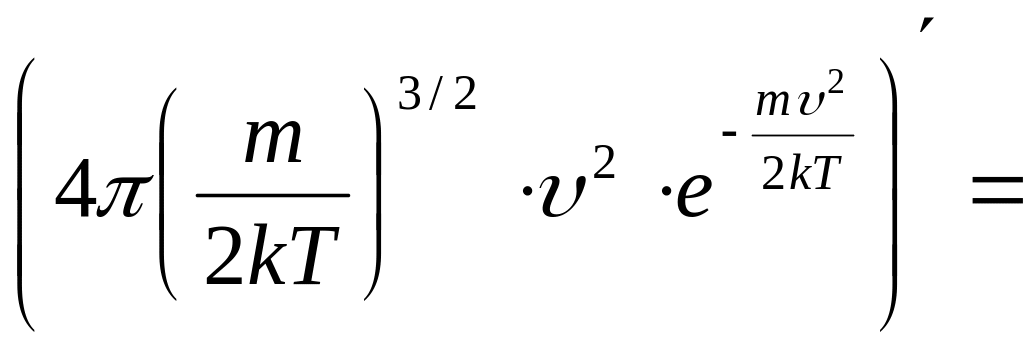 обозначим константу
обозначим константу
![]() и найдем производную произведения
и найдем производную произведения

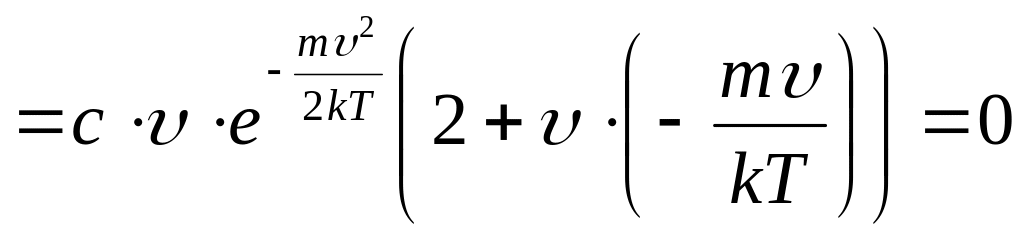
так как величина
![]() ,
то должно выполняться условие:
,
то должно выполняться условие:
![]() ,
, ![]() ,
, ![]()
![]() - скорость наиболее
вероятная.
- скорость наиболее
вероятная.
67. Подсчет числа молекул скорости, которых лежат в заданном диапазоне.
П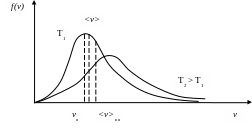 ри
комнатной температуре средняя
арифметическая скорость движения
молекул:
ри
комнатной температуре средняя
арифметическая скорость движения
молекул:
![]() ,
а характеристические скорости водорода
в 4 раза больше.
,
а характеристические скорости водорода
в 4 раза больше.
Как посчитать число молекул, скорости которых лежат в заданном диапазоне?
Если
![]() - число молекул в единице объема, то
- число молекул в единице объема, то
![]() - число молекул, скорости которых
распределены в интервале от
- число молекул, скорости которых
распределены в интервале от
![]() до
до
![]() равно:
равно:
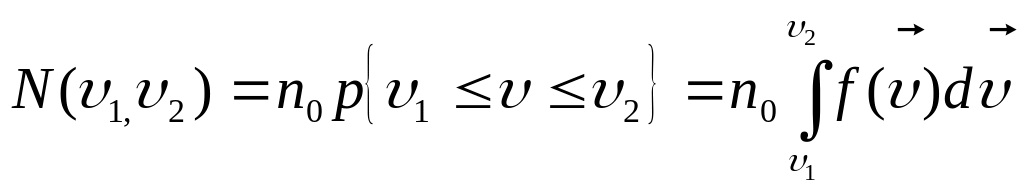 ,
если учесть что
,
если учесть что
![]() ,
и введя переменные
,
и введя переменные
![]() ,
,
![]() ,
,
![]() ,
,
![]() то
то
 - такой вид более
нагляден, для анализа формы кривой
распределения Максвелла. В книгах
имеются таблицы интеграла:
- такой вид более
нагляден, для анализа формы кривой
распределения Максвелла. В книгах
имеются таблицы интеграла:
![]() с их помощью упрощаются вычисления
величины
.
с их помощью упрощаются вычисления
величины
.
Из таблиц в частности находим, что:
![]() ;
; ![]() ;
;
![]()
Т.о. большая часть молекул имеет скорости в сравнительно небольшом интервале около наиболее вероятной, а молекул со скоростями вне этого интервала сравнительно мало.
