1.4 Волны де Бройля

Итак, имеются серьезные указания на то, что в природе микромира, по-видимому, важную роль играет принцип корпускулярно-волнового дуализма, т.е. в зависимости от конкретных условий и природы протекающего явления, один и тот же физический объект может проявлять и волновые, и корпускулярные свойства. Ранее мы проследили проявление этого дуализма для классически волнового объекта - электромагнитных волн (фотоэффект, испускание и поглощение света атомами). Естественно, если допустить, что корпускулярно-волновой дуализм является единым принципом существования материи на микроуровне, попытаться проследить его на объектах, которые классически мы привыкли воспринимать как частицы (корпускулы).

На сегодняшний день имеется богатый фактический материал, подтверждающий волновые проявления корпускул. Это, например, явление дифракции и интерференции пучков электронов или других частиц, это вся электронная микроскопия.

Однако когда впервые был поставлен вопрос об универсальности принципа корпускулярно-волнового дуализма, такого экспериментального материала не было. В отличие от гипотезы Планка, постулатов Бора, фотонов Эйнштейна, когда каждый из названных ученых имел возможность проверить свои полуквантовые построения на экспериментальных фактах, универсализация понимания принципа корпускулярно–волнового дуализма шла чисто умозрительным путем и, более того, впоследствии стала причиной проведения первых опытов по дифракции пучков электронов.

Честь распространения принципа корпускулярно-волнового дуализма на корпускулы (частицы) принадлежит французскому физику-теоретику Луи де Бройлю (1924г.)

Остановимся на основных моментах теории волн де Бройля.

Если резюмировать приложение корпускулярно-волнового дуализма к электромагнитным волнам, оно заключается в следующем: электромагнитные волны, излучение можно рассматривать как газ, состоящий из частиц (фотонов), причем имеет место следующее соответствие:

Волны характеризуются	Фотоны, кванты характеризуются
частотой ,	энергией ,
волновым вектором .	импульсом .

Де Бройль обращает это соответствие. Движение частицы предлагается рассматривать как распространение некоторой волны, причем имеет место следующее соответствие:

Частица характеризуется	Сопоставляемая волна характеризуется
энергией ,	частотой ,
импульсом .	волновым вектором .

В простейшем случае свободного движения частицы естественно сопоставить единственно истинно свободную волну – плоскую волну :

. (1.4.1)

Амплитудный множитель не существенен и может быть связан с выбором единицы энергии. Поэтому, по мере необходимости, мы будем переобозначать его любой константой. Кроме того, для простоты систему координат выберем таким образом, чтобы ось x была направлена вдоль импульса частицы. Тогда вместо формулы (1.4.1) запишем

. (1.4.2)

Это и есть волна де Бройля в простейшем случае свободно движущейся частицы. Как и любая волна, она характеризуется некоторой длиной волны де Бройля, которая, в соответствии с теорией плоских волн, может быть выражена следующим образом :

. (1.4.3)

В последнем равенстве знак приближения означает тот факт, что мы записали импульс, пользуясь классической механикой, тогда как к моменту появления работ де Бройля уже получила признание релятивистская механика специальной теории относительности. Там, где это будет необходимо, мы воспользуемся более точными релятивистскими соотношениями.

П режде чем приступить к детальному анализу идеологии волн де Бройля, заметим, что сопоставив электрону, вращающемуся в атоме по круговой орбите, волну де Бройля, можно прийти к уже известному условию квантования орбит (первый постулат Бора).

Допустим, что по орбите бежит плоская волна. Отметим ее фазу в некоторой точке . Для того, чтобы в результате интерференции не произошло самопогашение волны, необходимо, чтобы на орбите укладывалось целое число длин волн де Бройля, т.е.

. (1.4.4)

Приводя к общему знаменателю, имеем

(1.4.5)

что совпадает с выражением (1.3.27) (см. также рис. 1.4).

Теперь, пока с классических позиций, попытаемся установить, насколько полно можно описать частицу, посредством сопоставленной ей волны де Бройля.

Выясним с этой целью два вопроса по отношению к частице:

- Где находится частица в данный момент времени?

- С какой скоростью частица переносит энергию?

При траекторном описании движения (классическая механика) мы можем дать определенные ответы:

- Частица в данный момент времени имеет такую–то координату.

- Свободная частица несет с собой всю энергию, т.е. перенос энергии осуществляется со скоростью движения частицы .

Если же вместо частицы следить за соответствующей ей волной де Бройля, то на первый вопрос мы вообще не имеем ответа – истинно свободная, т.е. плоская волна, занимает все пространство. Что касается скорости переноса энергии, то в случае монохроматической волны она совпадает с фазовой скоростью, которую легче вычислить, проследив за распространением в пространстве и времени постоянной фазы волны (1.4.2) :

. (1.4.6)

Продифференцировав это соотношение ( и при свободном движении заданы), имеем

(1.4.7)

откуда, даже с помощью точных релятивистских соотношений, получаем

где (1.4.8)

что противоречит и заданной скорости переноса энергии частицей ( ), и релятивистской механике, согласно которой, скорости, превышающие скорость света, невозможны.

Таким образом, с одной стороны, принцип корпускулярно-волнового дуализма требует введения волн де Бройля; этого же требуют экспериментальные данные по дифракции пучков частиц. Косвенно (пусть не строго) волны де Бройля подтверждают постулат квантования орбит в водородоподобном атоме (по Бору). Но, с другой стороны, они не в состоянии описать движение частицы адекватным образом с точки зрения классической физики.

В поисках выхода из создавшегося положения возникла мысль о сопоставлении движущейся частице не одной волны де Бройля, а целой группы волн с некоторым разбросом по энергии и импульсу в окрестности истинных значений энергии и импульса частицы. Такую группу волн называют волновым пакетом. Этот шаг был вызван, с одной стороны, желанием сохранить за частицами волновые свойства, с другой стороны – тем фактом, что дифракционные картинки пучков электронов характеризуются некоторой размытостью максимумов и минимумов, т.е. дифрагирует как бы не одна волна, а несколько волн с близкими характеристиками.

Итак, сопоставим движущейся частице волновой пакет

. (1.4.9)

Для упрощения интерпретации волнового пакета разложим в точке в ряд Тейлора

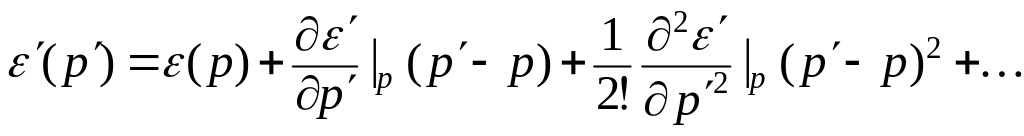(1.4.10)

Разброс волнового пакета по импульсу ( ) считаем достаточно малым, т.е. ряд (1.4.10), по предположению, достаточно быстро сходится. Тогда для простоты ограничимся в (1.4.10) первыми двумя слагаемыми ряда

. (1.4.11)

Введем новую переменную интегрирования

. (1.4.12)

Тогда вместо выражения (1.4.11) для волнового пакета имеем

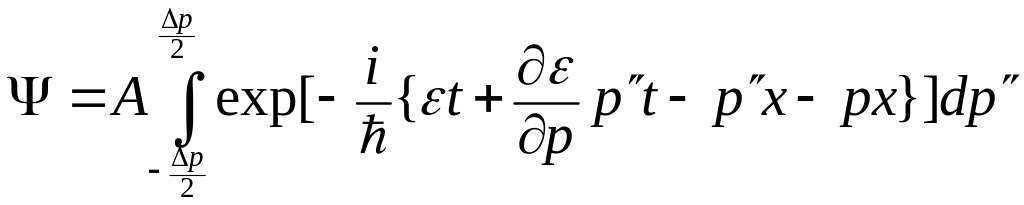. (1.4.13)

Вынося из-под интеграла величины, не зависящие от переменной интегрирования, получаем

. (1.4.14)

Теперь интеграл может быть легко взят и, переопределяя амплитудный множитель, имеем

(1.4.15)

.

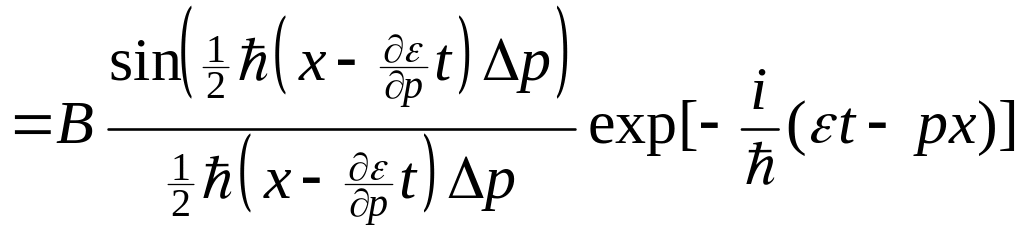Таким образом, волновой пакет (1.4.9) в принятом приближении можно рассматривать как плоскую волну де Бройля (экспоненциальный множитель в (1.4.15)) с пространственно-временной амплитудной модуляцией. Введя для простоты обозначение

(1.4.16)

вместо (1.4.15) можно записать

. (1.4.17)

Множитель

ведет себя как синусоида с убывающей амплитудой с ростом абсолютного значения . В нуле ( ), в соответствии с первым замечательным пределом, амплитудный множитель стремится к . И в пределах этого амплитудного значения первого множителя развивается волна де Бройля – второй множитель (см. рис. 1.5).

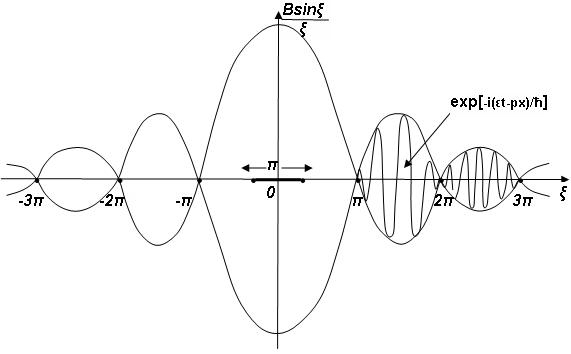
Амплитуда волнового пакета быстро уменьшается по мере удаления от первого максимума. Принимая условно, что волновой пакет сосредоточен в окрестности главного максимума порядка , получаем оценку локализации волнового пакета (для простоты делаем оценку в нулевой момент времени)

(1.4.18)

или

. (1.4.19)

Соотношение (1.4.19) известно как соотношение неопределенностей Гайзенберга. Теперь при ответе на вопрос, где находится частица, с помощью идеологии волнового пакета мы имеем более определенный ответ – в окрестности главного максимума порядка . Причем тем меньше, чем больше , и наоборот. В пределе одной волны де Бройля , но (плоская волна занимает все пространство).

Соотношение (1.4.19) можно трактовать и следующим образом: по-видимому не исключено, что в природе микромира имеются такие пары величин, которые мешают друг другу быть одновременно определенными (в данном случае – координата и импульс).

Обратимся теперь ко второму вопросу – с какой скоростью волновой пакет переносит энергию? Для группы волн известно, что энергия переносится с групповой скоростью, т.е. нужно проследить за распространением в пространстве и времени постоянного значения амплитуды. Последняя является функцией , и поэтому проследим за постоянным значением переменного множителя в определении , т.е. за

. (1.4.20)

Дифференцируя это выражение, имеем

(1.4.21)

откуда

. (1.4.22)

Обращаясь к релятивистскому определению энергии, имеем

, (1.4.23)

откуда приходим к выводу, что волновой пакет переносит энергию со скоростью частицы, которой он сопоставлен

. (1.4.24)

Итак, в принятом приближении (первые два члена ряда (1.4.10)) волновой пакет удовлетворительно решает вопрос о локализации частицы и скорости переноса энергии.

Остается лишь выяснить, какова в проведенных оценках погрешность, связанная с учетом последующих членов ряда (1.4.10).

Имея в виду исходное выражение для волнового пакета (1.4.9), оценим влияние третьего члена ряда (1.4.10) на локализацию волнового пакета, полагая, что при каких-то этот член может давать вклад

(1.4.25)

Учитывая соотношение (1.4.19) и то, что

(1.4.26)

окончательно получаем (численные множители, не влияющие на порядки производимых оценок, опускаем)

(1.4.27)

или для времени, в течение которого вклад в локализацию пакета за счет третьего члена ряда (1.4.10) станет порядка вклада предыдущего члена, имеем

. (1.4.28)

Оценим величину для реальных объектов. Возьмем, например, песчинку – макроскопический объект:

(1.4.29)

т.е. для макроскопического объекта волновой пакет практически сохраняет пространственную локализацию бесконечно долго. Заметим, что движение макрообъекта прекрасно описывается с помощью классической механики.

Обратимся далее к микрообъекту.

Рассмотрим, например, электрон.

(1.4.30)

т.е. волновой пакет изменяет свою локализацию за время и практически мгновенно, расплывается, не неся никакой информации о локализации электрона, которому он сопоставлен.

Таким образом, для микрообъектов, ради которых вводятся волны де Бройля, они не выдерживают критики. Это является еще одним стимулом создания принципиально новой теории движения микрообъектов – квантовой механики.

41