1.3 Линейчатые спектры атомов

В результате тщательного изучения спектров излучения атомов экспериментаторами было установлено, что они имеют линейчатый характер. Спектры простейших атомов (водорода, щелочных металлов) удовлетворительно описывались эмпирической формулой Бальмера, согласно которой дозволенные частоты в спектре отбираются по правилу

. (1.3.1)

Вскоре появились указания на то, что, по-видимому, для простейших атомов выполняется комбинационный принцип Ритца, согласно которому, если в спектре реализуется две частоты

(1.3.2)

то должна реализоваться и третья частота, равная разности исходных :

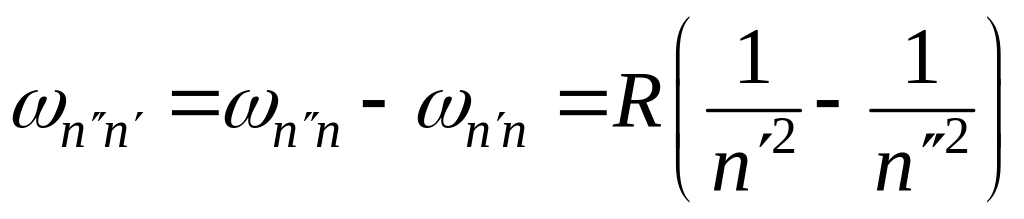. (1.3.3)

Во всех этих формулах (1.3.1) - (1.3.3) в качестве фигурирует известная из эксперимента спектроскопическая постоянная Ридберга.

В 1911г. были выполнены знаменитые опыты Резерфорда по рассеянию -частиц (ядра гелия) на тонких фольгах (на атомах). Для объяснения аномально большого количества отклонений -частиц на большие углы Резерфордом была предложена планетарная модель атома. По этой модели, основная масса атома сосредоточена в ядре очень малого размера ( ), несущем положительный заряд, вокруг которого вращаются электроны на расстояниях (размеры атома), несущие отрицательный заряд.

Классическая теория была не в состоянии объяснить формулы (1.3.1) - (1.3.3). В соответствии с законами классической физики, нельзя допустить планетарную модель атома. В самом деле, вращаясь вокруг ядра, т.е. двигаясь ускоренно (даже на строго круговой орбите при постоянной линейной скорости существует центростремительное ускорение), электрон должен излучать энергию, т.е. постепенно, потеряв всю свою энергию, упасть на ядро. Таким образом, классическая планетарная модель атома неустойчива, в то время как в природе атомы существуют сколь угодно долго.

Р ассмотрим классическое описание планетарной модели атома. Для простоты ограничимся водородоподобным атомом, т.е. таким атомом, у которого имеется ядро с зарядом и вокруг вращается один электрон. Это атомы изотопов водорода, однажды ионизированный гелий, дважды ионизированный литий и т.д. (см. рис. 1.3).

Ввиду того, что масса ядра много больше массы электрона (даже для легчайшего изотопа водорода ), считаем ядро покоящимся. Согласно классической механике две материальные точки взаимодействуют лишь посредством центральных сил – симметрия задачи предполагает, что поле, создаваемое ядром центрально симметрично, а траектория электрона всегда лежит в одной плоскости. В связи с этим будем использовать полярную систему координат ( координаты и ).

Кинетическая энергия электрона при этом имеет вид :

. (1.3.4)

Для потенциальной энергии двух притягивающихся зарядов запишем известное выражение кулоновской энергии :

. (1.3.5)

Лагранжиан в этом случае имеет вид

. (1.3.6)

Таким образом сформулирована классическая задача механики с двумя степенями свободы, т.е. необходимо решить систему двух уравнений Лагранжа (уравнения движения)

. (1.3.7)

В рассматриваемом случае для радиальной и угловой степеней свободы, в соответствии с (1.3.6) и (1.3.7), имеем следующие уравнения :

. (1.3.8)

Рассмотрение задачи начнем с угловой степени свободы. Лагранжиан (1.3.6) не содержит непосредственно переменной . Последняя входит в лагранжиан лишь через свою производную . Такие переменные в механике называются циклическими. Импульс, соответствующий циклической переменной, является интегралом движения. В самом деле, в соответствии с (1.3.6),

. (1.3.9)

Однако в этом случае из (1.3.6) следует

. (1.3.10)

Постоянство обусловлено симметрией задачи. В полярной системе координатах совпадает с моментом частицы относительно оси, проходящей через центр поля (начало координат) перпендикулярно координатной плоскости . Поскольку взаимодействие центральное, траектория плоская и .

Далее ограничимся простейшей траекторией электрона – круговой траекторией, т.е. рассмотрим движение при условии , или . Тогда в лагранжиане (1.3.6) исчезнет слагаемое – нет движения по радиальной переменной :

. (1.3.11)

Из выражения (1.3.11) следует

(1.3.12)

и, в соответствии с (1.3.8), получаем

. (1.3.13)

Данное соотношение может рассматриваться как аналитическое условие круговой орбиты. Поскольку мы приняли постоянство , а , , постоянны по определению, из соотношения (1.3.13) следует, что угловая скорость также постоянна, что автоматически ведет к постоянству полной энергии электрона (впрочем, энергия и без того является интегралом движения). Действительно,

, (1.3.14)

и, используя (1.3.13), получаем

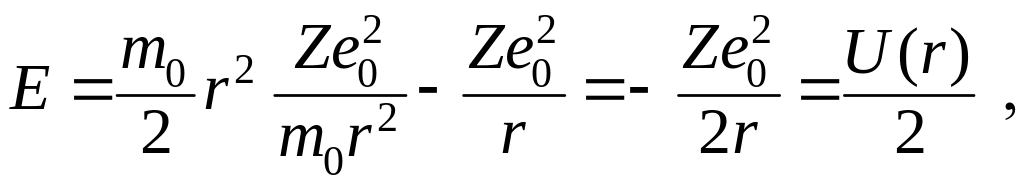(1.3.15)

что является константой при постоянном радиусе.

Введем далее формальным образом в рассмотрение адиабатический инвариант Эренфеста по циклической переменной , который, по определению, равен интегралу от циклического импульса по всему интервалу изменения циклической переменной :

. (1.3.16)

Выразим все характеристики электрона ( , , ) через адиабатический инвариант . При этом в качестве исходной системы уравнений принимаем условие круговой орбиты и определение адиабатического инварианта :

(1.3.17a)

(1.3.17b)

Для из выражений (1.3.17) имеем

, (1.3.18)

откуда

. (1.3.19)

Из (1.3.18) и (1.3.19) получаем

. (1.3.20)

Наконец, используя выражение (1.3.19), для полной энергии имеем

. (1.3.21)

Вспоминая, что угловая скорость, по определению, совпадает с циклической частотой

(1.3.22)

следует ожидать, что и частота излучения электрона, движущегося периодически по кругу, будет такой же. Возможно также излучение на обертонах, т.е. с частотами, кратными ,

. (1.3.23)

Однако это не объясняет экспериментальных данных по линейчатым спектрам атомов. Кроме того, и устойчивость атома по-прежнему не ясна.

В качестве основного классического результата для последующего рассмотрения укажем на очевидную формальную связь (1.3.20) и (1.3.21) :

. (1.3.24)

На значение в рамках классической механики нет никаких ограничений, а вместе с не существует ограничений и на выбор . Обе величины могут изменяться непрерывным образом, и, следовательно, под , в выражении (1.3.24) можно понимать как угодно малые величины.

Здесь уместно вспомнить, что, согласно Планку, физические величины, в частности, энергия, квантуются, т.е. имеется дозволенный природой ряд значений и, вообще говоря, как угодно малое в (1.3.24) необходимо заменить конечным приращением , соответствующим дозволенным энергиям. Заметим однако, что с выбором дозволенных автоматически квантуются также , и , т.е. фиксируются дозволенные орбиты. Заменяя (1.3.24) соответствующим соотношением в терминах конечных приращений, получим

(1.3.25)

откуда обнаруживаем, что реализацию излучения с частотой следует понимать связанной не с движением по конкретной дозволенной орбите, а с изменением одной орбиты на другую, сопровождаемым соответствующим изменением энергии. Движение по конкретной дозволенной орбите не приводит к излучению в духе (1.3.25).

Таким образом, от гипотезы Планка мы переходим к следующим утверждениям:

1. Электрон движется по дискретным дозволенным орбитам, находясь на которых, он не излучает и не поглощает энергию, т.е. электрон имеет ряд дозволенных стационарных энергетических состояний.

1. При переходе из одного энергетического состояния в другое (с одной орбиты на другую) атом излучает или поглощает энергию.

Но это и есть два знаменитых постулата Бора (1913г.). Остается дополнить их количественными соображениями.

Минимальная поглощаемая или испускаемая порция энергии (квант), согласно гипотезе Планка, . Отсюда, согласно (1.3.25),

. (1.3.26)

Из соображений размерности и совпадения частот в левой и правой частях этого соотношения, имеем

. (1.3.27)

Это условие есть не что иное, как боровское квантование (выбор) дозволенных орбит. Заметим, что частота, фигурирующая в выражениях (1.3.25) и (1.3.26), не имеет никакого отношения к частоте движения по орбите (1.3.21). Переход от бесконечно малых приращений (1.3.24) к конечным, хотя и малым, приращениям приводит к качественному изменению содержания, к различию сущности соотношений (1.3.24) и (1.3.25). (Блестящий пример известного закона диалектики о переходе количества в качество!)

Соотношение (1.3.26) мы записали для соседних орбит, т.е.

. (1.3.28)

Однако нет никаких оснований, допуская возможность перехода электрона с одной орбиты на другую для соседних орбит, запретить эти переходы для произвольных орбит. При этом для произвольных орбит вслед за гипотезой Планка естественно принять

. (1.3.29)

Таким образом, мы имеем количественное выражение постулатов Бора ((1.3.27) и (1.3.29)). Исходя из выражений (1.3.27), (1.3.29) и (1.3.21), получаем для отбора орбит и соответствующих значений энергий следующие выражения :

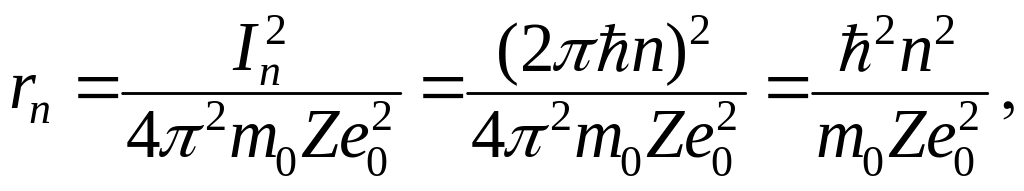(1.3.30)

. (1.3.31)

В частности, для атома водорода

(1.3.32)

что соответствует экспериментальным данным по размерам атомов. Для энергии в случае атома водорода имеем

. (1.3.33)

Вычисляя дозволенные частоты соответствующего спектра по формуле (1.3.29), получаем

. (1.3.34)

Это и есть формула Бальмера. Заметим, что спектроскопическая постоянная Ридберга выражена через другие известные постоянные, в том числе постоянную Планка:

. (1.3.35)

Проведенное рассмотрение полуквантовой теории водородоподобного атома (внедрение гипотезы Планка в классическое описание) лишний раз показывает, что в будущей теории микромира должно быть естественное место квантованию физических величин (здесь – энергии и адиабатического инварианта) и карпускулярно-волновому дуализму (электромагнитное излучение - свет - испускается и поглощается квантами – фотонами).