Глава 1. Основные предпосылки создания квантовой механики

1.1 Свойства равновесного излучения

1.1.1 Классическое описание

Рассмотрим свойства равновесного излучения в рамках классической теоретической физики. К понятию равновесного излучения можно прийти на основе следующего эксперимента. Пусть имеется некоторое массивное (макроскопическое) тело с полостью (см. рис. 1.1), которое нагревается до температуры T (абсолютная шкала). При этом электроны, находящиеся в стенке полости, за счет интенсивного теплового движения излучают электромагнитные волны. Подчеркнем, что эксперимент сейчас осмысливается наивно классически. В самом деле, движение электронов финитное, так как эксперимент не приводит к разрушению тела, т.е. электроны не уходят на бесконечность. А поскольку финитное движение всегда ускоренное, то электроны (в соответствии с законами классической электродинамики) излучают, и полость заполняется излучением.

В свою очередь, излучение через силу Лоренца влияет на движение электронов и отдает им часть своей энергии обратно. При заданной температуре T устанавливается некоторое равновесное состояние, когда взаимный обмен энергией в обе стороны скомпенсирован. Отсюда название излучения, заполняющего полость, – равновесное излучение. Другое название – излучение абсолютно черного тела. Последнее название является несколько условным.

Классический эксперимент позволяет установить некоторые закономерности, имеющие место для равновесного излучения. Это закон Стефана–Больцмана, который утверждает, что полная плотность равновесного излучения пропорциональна четвертой степени температуры:

, (1.1.1.1)

Второй экспериментально обнаруженный закон, закон смещения Вина, связывающий длину волны λ_max , на которую приходится максимум энергии равновесного излучения, с температурой :

(1.1.1.2)

Кроме того, экспериментально был достаточно подробно изучен спектральный состав равновесного излучения. Классическая теория хотя и давала в какой–то мере объяснение названных закономерностей, но не могла объяснить, в частности, количественных значений констант и и характера спектральной плотности равновесного излучения (плотности энергии излучения, приходящейся на единичный интервал частоты при данном значении частоты ω).

Рассмотрим равновесное излучение с точки зрения классической теоретической физики.

Сначала дадим анализ физики электрона, колеблющегося в стенке полости массивного тела в нашем эксперименте. Для простоты будем считать, что он совершает линейные колебания, хотя истинный характер финитного движения может быть гораздо более сложным. Механическое уравнение свободных колебаний материальной точки (электрона) имеет вид

(1.1.1.3)

Здесь система координат выбрана таким образом, что ось направлена вдоль линии колебаний электрона; – частота свободных колебаний электрона. Однако в этом уравнении не учтено влияние излучения на характер движения электрона. Поэтому в правой части необходимо записать силу Лоренца. Поскольку нас будет интересовать в конечном итоге лишь энергия электрона, влияние магнитной компоненты излучения на движение электрона не учитываем. Тогда вместо уравнения (1.1.1.3) имеем

(1.1.1.4)

где – электрическая напряженность равновесного электромагнитного излучения в направлении , – заряд электрона, – его масса покоя.

Поскольку равновесное излучение реализуется на разных частотах, в общем случае представим в виде ряда Фурье по частотам:

(1.1.1.5)

Допуская, что достаточно мала, можно считать, что Фурье-представление (1.1.1.5) учитывает практически все возможные частоты ( для соседних достаточно близки друг к другу). Заметим, в частности, что в правой части (1.1.1.5) возможно наличие частоты, совпадающей с частотой собственных колебаний электрона ( ). В этом случае, как известно, совпадение частоты вынуждающей силы с собственной частотой колебаний электрона, в соответствии с уравнением (1.1.1.4), приводит к резонансу с бесконечной амплитудой колебаний и, следовательно, уравнение (1.1.1.4) не может адекватно описывать рассматриваемый процесс. Резонанса можно избежать, если учесть потери энергии электроном на лучистое трение (излучение). Тогда уравнение (1.1.1.4) необходимо дополнить соответствующим слагаемым:

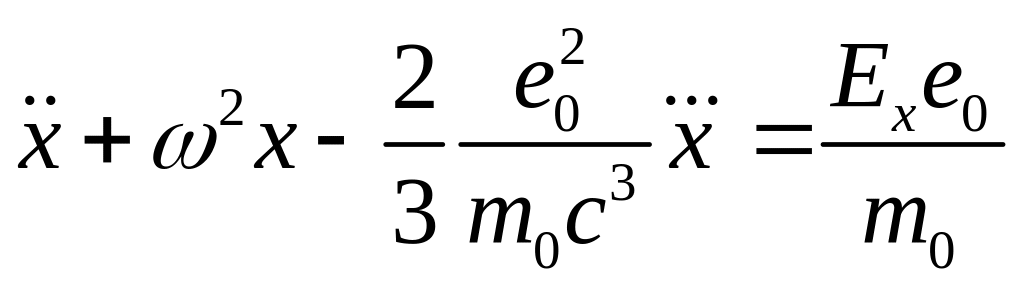. (1.1.1.6)

Здесь – сила лучистого трения, отнесенная к единице массы. В последнем уравнении учтено влияние излучения на движение электрона через силу Лоренца – правая часть, и обратно – подпитка равновесного излучения электроном за счет потерь энергии на лучистое трение.

Прежде, чем приступить к решению уравнения (1.1.1.6), укажем одно полезное свойство Фурье-коэффициентов при представлении физической величины в виде ряда Фурье. Итак, пусть некоторая физическая величина , зависящая от времени, представлена рядом Фурье. Тогда имеем

(1.1.1.7)

Вспоминая, что любая физическая величина действительна, необходимо потребовать

(1.1.1.8)

Займемся теперь решением уравнения (1.1.1.6). Правая часть уравнения является суперпозицией различных гармоник. В соответствии с теорией обыкновенных линейных дифференциальных уравнений можно утверждать, что и решением (1.1.1.6) будет суперпозиция тех же гармоник :

, (1.1.1.9)

причем, согласно (1.1.1.8), . Подставляя (1.1.1.5) и (1.1.1.9) в уравнение (1.1.1.6), получаем

(1.1.1.10)

Так как различные гармоники представляют собой линейно независимые функции, то уравнение (1.1.1.10) выполняется тождественно для каждой гармоники в отдельности :

(1.1.1.11)

Отсюда

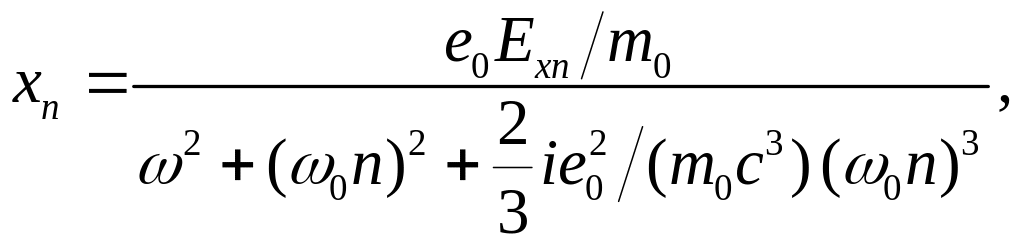(1.1.1.12)

и в качестве решения уравнения(1.1.1.6) принимается следующая суперпозиция гармоник :

(1.1.1.13)

Имея закон движения электрона (1.1.1.13), согласно теореме вириала, нетрудно вычислить среднее по времени значение его энергии

(1.1.1.4)

Получим вспомогательное выражение, позволяющее возводить в квадрат и усреднять по времени ряд Фурье:

(1.1.1.15)

Так как

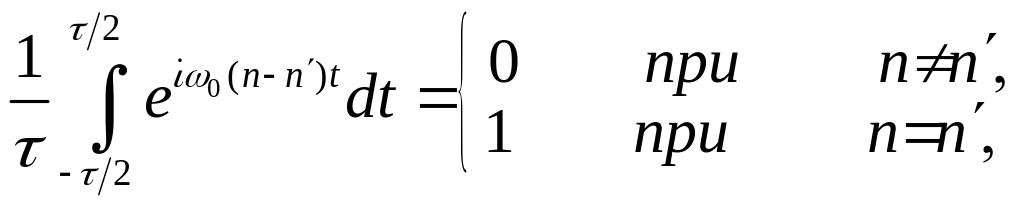(1.1.1.16)

из преобразования (1.1.1.15) окончательно имеем

. (1.1.1.17)

Здесь для простоты записи переопределен нулевой коэффициент Фурье

(F₀ → 2F₀).

В соответствии с (1.1.1.17) из (1.1.1.13) и (1.1.1.14) получаем

(1.1.1.18)

Полученное выражение имеет явную резонансную структуру. В самом деле, если не учитывать лучистое трение (последнее слагаемое в знаменателе (1.1.1.18)), то при ω₀n = ω имеем бесконечный резонанс. Учет лучистого трения устраняет эту бесконечность, но резонанс остается очень сильным, так как величина лучистого трения крайне мала. Оценивая порядки величин, имеем

Поэтому ощутимый вклад в среднее значение энергии дают лишь частоты, близкие к резонансным.

Перейдем в выражении (1.1.1.18) от суммирования к интегрированию, введя переменную частоту, т.е. в качестве переменной интегрирования принимаем

(1.1.1.19)

Тогда

(1.1.1.20)

Из условия резонанса имеем

, (1.1.1.21)

откуда вместо (1.1.1.20) получаем

(1.1.1.22)

Используя (1.1.1.19) – (1.1.1.22), заменяем в (1.1.1.18) суммирование интегрированием. При этом, поскольку вклад в дают в основном частоты, близкие к ω, считаем амплитуду постоянной по области интегрирования, то есть заменяем . Эта, безусловно, не строгая процедура вносит некоторую погрешность, которой можно пренебречь ввиду огромной амплитуды резонанса. Таким образом, резонансный пик в (1.1.1.18) мы заменяем как бы прямоугольным выбросом. Итак,

(1.1.1.23)

Введем новую переменную интегрирования :

, (1.1.1.24)

Здесь вновь учтено, что существенны лишь частоты . Распространяя область интегрирования на всю ось ξ (что опять же возможно в рамках принятого приближения), имеем

(1.1.1.25)

Заметим, что последнее выражение получено в рамках классической механики. Полученное определение среднего по времени значения энергии электрона

(1.1.1.26)

содержит, однако, величины, не наблюдаемые экспериментально; , и .

Опишем теперь на основе законов классической физики электромагнитное излучение, заполняющее полость в рассматриваемом эксперименте. Для плотности энергии излучения, в соответствии с классической термодинамикой, можно записать

(1.1.1.27)

В соответствии с (1.1.1.19) – (1.1.1.21) можем перейти от суммирования к интегрированию и, учитывая (1.1.1.17), имеем

(1.1.1.28)

С другой стороны, если бы была известна спектральная плотность энергии равновесного излучения (количество энергии излучения в единице объема при частоте ω в единичном интервале частот), мы могли бы записать

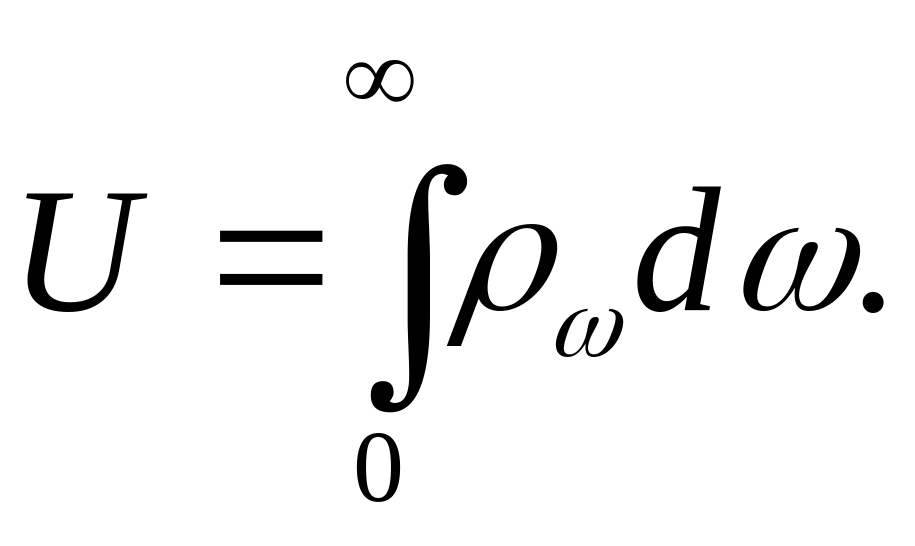(1.1.1.29)

Сравнивая выражения (1.1.1.28) и (1.1.1.29), определяем спектральную плотность энергии равновесного излучения

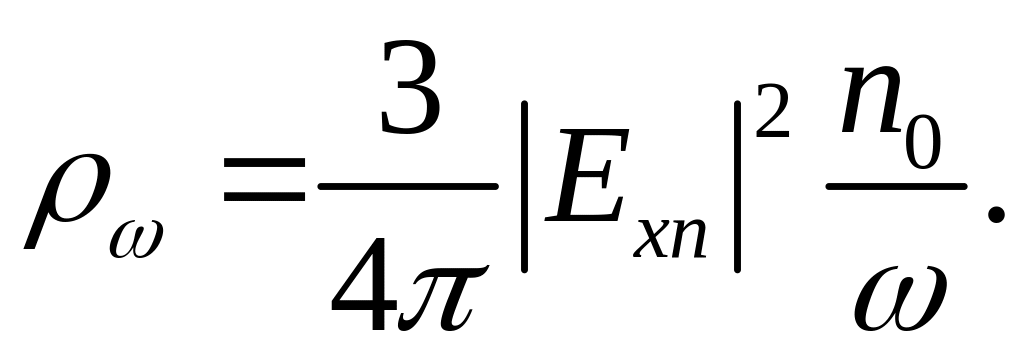(1.1.1.30)

Учитывая (1.1.1.30) и (1.1.1.26), получаем связь спектральной плотности энергии излучения со средней энергией электрона :

(1.1.1.31)

В этом выражении остается лишь одна экспериментально не наблюдаемая величина .

В связи с этим вспомним, что при получении мы проследили за закономерностями движения одного электрона с последующим усреднением по времени.

С другой стороны, рассматриваемый эксперимент существенно макроскопичен, т.е. в формировании равновесного излучения принимает участие достаточно большое число электронов; во всяком случае достаточно большое для выполнения законов статистической физики. Поэтому уместно вспомнить основную аксиому статистики, согласно которой среднее по ансамблю равно среднему по времени (эргодическая гипотеза). Распределение электронов по энергиям задается известной формулой Больцмана :

(1.1.1.32)

Здесь – постоянная Больцмана. Усредняя по этому распределению (по ансамблю), получаем

(1.1.1.33)

Подставляя этот результат в выражение спектральной плотности энергии (1.1.1.31), приходим к знаменитой формуле Рэлея-Джинса

(1.1.1.34)

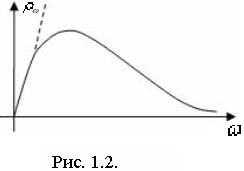
Эта формула известна как лучший классический результат для описания равновесного излучения. Проанализируем этот результат. Прежде всего, укажем, что формула Рэлея–Джинса удовлетворительно согласуется с экспериментальными данными в области малых частот (см. рис. (1.1.1.2)). Кроме того, укажем, что этот результат согласуется с известным термодинамическим законом Вина, полученным классически для объяснения закона смещения Вина (1.1.1.2) :

(1.1.1.35)

З

аметим, что вид функции классическая термодинамика определить не может. Согласие между выражениями (1.1.1.34) и (1.1.1.35) очевидно

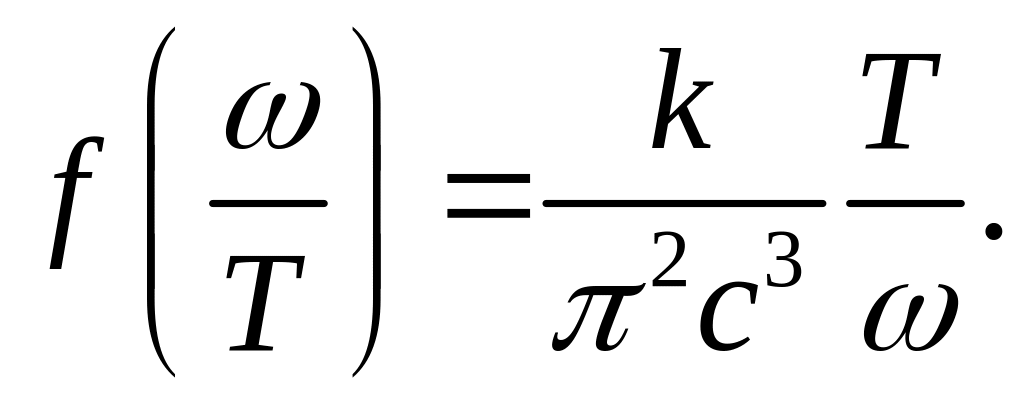(1.1.1.36)

Однако в области больших частот формула Рэлея-Джинса не в состоянии описать экспериментальные данные. Спектральная плотность энергии равновесного излучения, в соответствии с формулой Рэлея-Джинса, с ростом частоты неограниченно возрастает, тогда как экспериментальная кривая асимптотически стремится к нулю. Кроме того, полная плотность равновесного излучения, вычисленная на основе (1.1.1.34), также расходится

(1.1.1.37)

Этот результат, известный в литературе как ультрафиолетовая катастрофа, противоречит здравому смыслу. Конечное число электронов в стенке полости массивного тела в нашем эксперименте создает в единице объема (объем также конечен) бесконечную энергию. Такой результат не может быть принят как удовлетворительный с материалистической точки зрения.

Итак, лучшее классическое описание равновесного излучения – формула Рэлея-Джинса – не выдерживает прежде всего теоретико-материалистической критики (ультрафиолетовая катастрофа) и, кроме того, не согласуется с экспериментальными данными в области высоких частот.

Поскольку классическая теория не может предложить ничего лучшего, необходимо искать выход за рамками классической теоретической физики.