Вопрос 44. Статистический критерий проверки гипотез. Алгоритм проверки статистических гипотез.

Статистический критерий — строгое математическое правило, по которому принимается или отвергается статистическая гипотеза. Алгоритм проверки:

1. Формулируется нулевая гипотеза Н₀ о распределении вероятностей на множестве Х.

2. Задаётся некоторая статистика (функция выборки) T: Xm →R , для которой выводится функция распределения и/или плотность распределения.

3. Фиксируется уровень значимости.

4. На множестве допустимых значений статистики T выделяется критическое множество наименее вероятных значений статистики T.

5. Собственно статистический тест (статистический критерий).

Вопрос 45. Проверка гипотезы о равенстве двух выборочных средних независимых выборок. Большие независимые выборки.

При проверке гипотезы о существенности или несущественности различия двух выборочных средних можно применить критерий Стьюдента (при условии достаточно больших объёмов выборок (n≥30).

Уровень значимости t-критерия равен вероятности ошибочно отвергнуть гипотезу о равенстве выборочных средних двух выборок. При проверке разности двух средних с помощью t-критерия Стьюдента используется следующий алгоритм:

1. Записать вариационный ряд результатов Х экспериментальной группы.

2. Записать вариационный ряд результатов Y контрольной группы.

3. Найти выборочные средние двух выборок.

4. Найти выборочные дисперсии Dx и Dy.

5. Вычислить эмпирическое значение критической статистики

6. Определить по таблице критическое значение для соответствующего уровня.

При больших объемах выборок вместо таблиц распределения Стьюдента достаточно пользоваться таблицами стандартного нормального распределения Ф(х).

Вопрос 46. Проверка гипотезы о равенстве двух выборочных средних независимых выборок. Малые независимые выборки.

См. вопрос 45.

Вопрос 47. Проверка гипотезы о равенстве дисперсий двух независимых выборок.

Пусть есть две независимые выборки значений нормально распределенной величины x: х1, х2, ..., xn - всего n элементов, и нормально распределенной величины y: y1, y2, ..., ym - m элементов. Гипотеза Н₀ состоит в том, что дисперсии величин Х и У равны, т.е. Н₀: Dx = Dy = σ²

Эта гипотеза проверяется по следующему критерию. Случайная величина , где и распределена по закону, получившему название "распределение Фишера" или "F-распределение".

Вопрос 48. Оценка средней разности двух зависимых выборок.

Для оценки средней разности между сред. значениями 2 зависимых выборок величины D рассм. как наблюдения, принадлежащие 1 и той же выборке. Если стандартное отклонение разностей известно, применяется Z-критерий, вычисляемый по формуле:

Он основан на нормированном нормальном распределении статистики критерия.

Вопрос 49. Проверка гипотезы о равенстве среднего значения выборки определенному числу.

Гипотеза Н0: – среднее значение генеральной совокупности 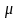, из которой получена выборка, равно данному значению. Уровень значимости: . Чтобы проверить данную гипотезу, применяют Т-критерий:

1. Принимается предположение о нормальности, формулируются гипотезы Н0 и H1 задается уровень значимости .

2. Получают выборку объема n.

3. Вычисляется выборочное среднее арифметическое и исправленная выборочная дисперсия (S²).

4. Определяется значение t-критерия по формуле:

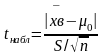
5. По таблицам находится t _критич – критическое значение t-критерия при уровне значимости и числе степеней свободы n=n–1

6. Делается вывод: если t _набл > t _критич, то выборочное среднее значимо отличается от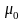 на уровне значимости , следовательно отклоняется гипотеза Н₀