Вопрос 13. Дисперсия случайной дискретной величины и ее свойства.

Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Пусть X - случайная величина, определённая на некотором вероятностном пространстве. Тогда: 1) D(X) = M (X₂) – (M[X])² Где M - математическое ожидание

2) Дисперсия любой случайной величины неотрицательна: D[– X]= D[X]

3) Если дисперсия случайной величины конечна, то конечно и её математическое ожидание;

4) Если случайная величина равна константе, то её дисперсия равна нулю: D[a] = 0

Вопрос 14. Одинаково распределенные взаимно-независимые случайные величины.

Рассмотрим n взаимно независимых случайных величин X₁,Х₂,...,Х_n, которые имеют одинаковые распределения и одинаковые характеристики.

1. Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию (а) каждой из ветчин:

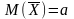
2. Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в n раз меньше дисперсии D каждой из величин:

3. Среднее квадратическое отклонение среднего арифметического n одинаково распределенных взаимно независимых случайных величин в √n раз меньше среднего квадратического отклонения, а каждой из величин:

Вопрос 15. Интегральная функция распределения вероятностей и ее свойства.

Интегральной функцией распределения называют функцию F(x), определяющую для каждого значения x случайной величины X вероятность того, что величина X примет значение, меньшее x, то есть F(x) = P(X < x).

Интегральная функция распределения имеет следующие свойства.

1. Значения интегральной функции принадлежат отрезку (0,1): 0 і F(x) і 1. Следовательно, график интегральной функции распределения расположен в полосе, ограниченной прямыми y = 0, y = 1.

2. F(x) - неубывающая функция, то есть F(x2) і F(x1), если x2 > x1. Следовательно, при возрастании x в интервале (a, b) интегральной функции распределения поднимается вверх.

Вопрос 16. Дифференциальная функция распределения вероятностей и ее свойства.

Дифференциальной функцией распределения называется 1-я производная от интегральной функции распределения. f(X) = F ’ (X)

Свойства дифференциальной функции распределения

1) f(X) ≥ 0 , т.к. это производная от неубывающей функции.

2)

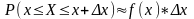
3)

Вопрос 17. Числовые характеристики непрерывных случайных величин.

1) Плотностью распределения вероятностей называют первую производную от функции распределения.

f(X) = F ’ (X)

2) Математическое ожидание определяется как:

3) Модой М₀(Х) непрерывной случайной величины называю наиболее часто повторяющееся значение признака.

4) Дисперсия определяется по формуле:

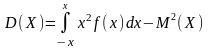
5) Среднее квадратическое отклонение:

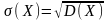
Вопрос 18. Равномерное распределение.

Равномерным называется распределение вероятностей непрерывной случайной величины X, если на интервале (a,b), которому принадлежат все возможные значения X, плотность распределения сохраняет постоянное значение:

Функкция распределения имеет вид:

Вопрос 19. Показательное распределение.

Показательным называют распределение вероятностей непрерывной случайной величины X, которое описывается полностью:

Функция распределения показательного закона:

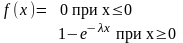
Вопрос 20. Нормальное распределение.

Нормальным называется распределение вероятностей непрерывной случайной величины X, плотность которого имеет вид:

Вероятность того, что случайная величина X примет значение, принадлежащее интервалу ( ; ):

Вопрос 21. График нормального распределения. Исследование кривой Гаусса.

В зависимости от изменения параметров a и график распределения изменяется так: при увеличении параметра a график будет перемещаться вдоль оси x вправо. При уменьшении – влево. С возрастанием распределение убывает. С уменьшением кривая > островершинная и растягивается в направлении оси oy. График называют кривой Гаусса.

Вероятность того, что X примет значение, принадлежащее интервалу ( ; ):