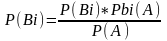- •Вопрос 1. Предмет и основные понятия теории вероятностей.
- •Вопрос 2. Определение вероятности события. Свойства вероятности события.
- •Вопрос 3. Основные формулы комбинаторики.
- •Вопрос 4. Теоремы сложения и умножения вероятностей.
- •Вопрос 5. Теорема наступления хотя бы 1 события и следствие к ней.
- •Вопрос 6. Теорема о полной вероятности и формула гипотез Бейеса:
- •Вопрос 7. Формула Бернулли. Наивероятнейшее число наступления событий в независимых испытаниях. Формула Пуассона.
- •Вопрос 8. Локальная и интегральная формулы Лапласа.
- •Вопрос 9. Вероятность отклонения относительной частоты от постоянной вероятности.
- •Вопрос 10. Случайные величины и их виды. Дискретная случайная величина.
- •Вопрос 11. Математическое ожидание дискретной случайной величины и его свойства.
- •Вопрос 12. Действия над случайными величинами.
- •Вопрос 13. Дисперсия случайной дискретной величины и ее свойства.
- •Вопрос 14. Одинаково распределенные взаимно-независимые случайные величины.
- •Вопрос 15. Интегральная функция распределения вероятностей и ее свойства.
- •Вопрос 22. Вероятность попадания нормально-распределенной случайной величины в заданный интервал. Вероятность заданного отклонения. Правило трех сигм.
- •Вопрос 23. Специальные законы распределения.
- •Вопрос 24. Функции одного случайного аргумента.
- •Вопрос 32. Основные задачи математической статистики.
- •Вопрос 33. Предмет и методы матем. Статистики. Основные понятия матем. Статистики.
- •Вопрос 34. Определение и виды вариационных рядов. Графическое изображение вариационных рядов.
- •Вопрос 35. Средняя арифм. Ряда распределения и ее свойства. Мода и медиана ряда распределения.
- •Вопрос 36. Дисперсия ряда распределения и ее свойства. Среднее квадратич. Отклонение. Коэф. Вариации.
- •Вопрос 37. Моменты ряда распределения и связь между ними. Асимметрия и эксцесс ряда распределения.
- •Вопрос 38. Сущность выборочного метода. Характеристики выборочной и генеральной совокупности.
- •Вопрос 39. Ошибки, возникающие в выборочном наблюдении.
- •Вопрос 40. Статистические оценки выборочной совокупности и их свойства.
- •Вопрос 41. Точечные и интервальные оценки. Доверительная вероятность, доверительный интервал.
- •Вопрос 42. Определение необходимой численности выборки. Распространение данных выборки на генеральную совокупность.
- •Вопрос 43. Понятие и виды статистических гипотез. Ошибки 1-го и 2-го рода. Уровень значимости и мощности критерия.
- •Вопрос 44. Статистический критерий проверки гипотез. Алгоритм проверки статистических гипотез.
- •Вопрос 45. Проверка гипотезы о равенстве двух выборочных средних независимых выборок. Большие независимые выборки.
- •Вопрос 46. Проверка гипотезы о равенстве двух выборочных средних независимых выборок. Малые независимые выборки.
- •Вопрос 47. Проверка гипотезы о равенстве дисперсий двух независимых выборок.
- •Вопрос 48. Оценка средней разности двух зависимых выборок.
- •Вопрос 49. Проверка гипотезы о равенстве среднего значения выборки определенному числу.
- •Вопрос 50. Формы и виды корреляционной зависимости.
- •Вопрос 51. Основные этапы корреляционно-регрессионного анализа.
- •Вопрос 52. Определение параметров однофакторного уравнения регрессии.
- •Вопрос 53. Оценка тесноты связи между признаками.
- •Вопрос 54. Оценка значимости величины показателей регрессии и корреляции.
Вопрос 1. Предмет и основные понятия теории вероятностей.
Т.В. – математическая наука, изучающая закономерности случайных процессов. Предметом теории вероятностей являются события, которые разделяют на 3 вида: достоверные, невозможные и случайные.
- Достоверным называется событие, которое обязательно произойдет.
- Невозможным называют событие, которое не может произойти.
- Случайным называют событие, которое может произойти, а может и не произойти.
Осуществление комплекса условий называется опытом (испытанием). Результат опыта – событие.
- 2 события совместны, если появление 1 из них не исключает появление другого. Иначе – несовместные.
- События называют единственно возможным, если должно произойти хотя бы 1 из них.
Вопрос 2. Определение вероятности события. Свойства вероятности события.
Вероятность события А равна отношению числа исходов, благоприятствующих появлению данного события к общему числу исходов испытания. Р(А) = m/n
- Вер-ть достоверного события = 1, т.к. m=n
- Вер-ть невозможного события = 0, т.к. m=0
- Вер-ть случайного события находится в пределах от 0 до 1 включительно.
Свойства вероятности событий:
0 ≤ P(A) ≤ 1 для любого события A
P(A) + P(Ā) = 1
P(A+B) = P(A) + P(B)
P(AB) = P(A)*P(B) (совместное наступление 2 не ~ событий)
P(A) = 1 – P(Ā1)*P(Ā2)* P(Ān) (хотя бы 1 событие)
Вопрос 3. Основные формулы комбинаторики.
Существует 3 типа соединений: сочетание, перестановка и размещение.
1) Сочетаниями
называются комбинации, состоящие из n
элементов по m элементов
каждый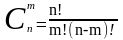
2) Размещениями называются комбинации, состоящие из n элементов по m элементов каждый, которые отличаются друг от друга либо составом, либо размещением.
3)
Размещениями называются комбинации,
состоящие из n элементов по m элементов
каждый, которые отличаются друг от друга
либо составом, либо размещением.
Вопрос 4. Теоремы сложения и умножения вероятностей.
Теорема сложения вероятностей
Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий:
Р (А + В) = Р (А) + Р (В)
В случае, когда события А и В совместны, вер-ть их суммы выражается формулой
Р (А +В) = Р (А) + Р (В) – Р (АВ)
Теорема умножения вероятностей
Вероятность произведения двух событий равна вер-ти одного из них, умноженной на условную вероятность другого при наличии первого: Р(АВ) = Р(А) · Р(В/А), или Р (АВ) = Р(В) · Р(А/В)
Вопрос 5. Теорема наступления хотя бы 1 события и следствие к ней.
Теорема: Вероятность появления хотя бы одного из событий А1 , А2 , ..., Аn , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
Р(A) = 1 — q1q2 ... qn
Следствие: Если события Ai имеют одинаковую вероятность появиться p, то вероятность появления хотя бы 1 события из n не зависимых испытаний: P(A) = 1 - qn где p+q=1
Вопрос 6. Теорема о полной вероятности и формула гипотез Бейеса:
Теорема: Пусть событие А может появиться вместе с одним из попарно несовместных событий, образующих полную группу событий. Тогда вероятность наступления события A определяется по формуле:
P(A) = P(B1) * PB1(A) + P(B2) * PB2(A) + … + P(Bn) * PBn(A)
Формула
Бейеса: