23.Прямая на плоскости.Уравнение с угловым коэффициентом.Общее уравнение прямой.Неполные уравнения.

Прямая на плоскости в декартовой системе координат задается уравнением первой степени относительно х и у.

Уравнение прямой с угловым коэффициентом.

Y=Y₀+k(x-x₀) , x₀-данная точка, к-угловой коэффициент ,равный тангенсу угла между прямой и осью ОХ.Y₀-точка пересечения прямой и оси ОУ.

Общее уравнение прямой:

А(у-у₀)+В(х-х₀)=0 прямая, проходящая через данную точку перпендикулярно данному вектору. Ах+Вх+С=0 , где (А;B)- координаты нормального вектора.

Неполное уравнение прямой- общее уравнение, в котором один или несколько коэффициентов равны нулю.

Если А=0, прямая параллельна ОХ

Если В=0, прямая параллельна оси ОУ

Если С=0, прямая проходит через начало координат

Если А=0 и С=0 или В=0 и С=0, прямая совпадает с неравной нулю осью.

24.Уравнение прямой через две точки,каноническое,параметрическое.

Через две точки:

=

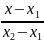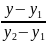
Каноническое:

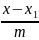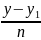= ,где (m;n) координаты сонаправленное вектора)

Параметрическое:

К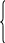 огда

=t => х=mt+x₀

=t => y=nt+y₀

25.Уравнение прямой в отрезках. Нормальное уравнение прямой.

Если прямая пересекается с осями координат, в общем уравнении прямой х или у равны нулю,тогда:

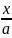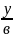+ =1 –уравнение прямой в отрезках.

Нормальное уравнение прямой:

X*sin a + y*cos a –P=0 , где Р-длина перпендикуляра, опущенного на прямую из начала координат, а-угол между перпендикуляром и осью ОХ.

26.Расстояние от точки до прямой на плоскости.Взаимное расположение прямых.Угол между прямыми.

D(M₀ l)=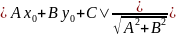 , где (А;В)- координаты нормального ветора.

Взаимное расположение прямых:

1.Паралельность

Прямые параллельны,если отношение одноименных координат нормальных векторов равно.

2.Перпендикулярность:

Прямые перпендикулярны,если сумма произведений одноименных координат нормальных векторов этих прямых равна нулю.

3.Угол между прямыми.

Тангенс угла между прямыми раен произведению их угловых коэффициентов,поделенный на сумму единицы и произведение угловых коэффициентов.

4.Пересечение.

27.Эллипс

Эллипс-геометрическое место точек, для каждой из которых сумма расстояний между двумя данными точками плоскости,называемых фокусами есть константа и больше,чем расстояние меджу фокусами.

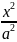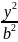+ =1 - Каноническое уравнение эллипса, где а- длина большой полуоси, b- длина малой полуоси, b<a-горизонтальная,a<b-вертикальная.

x²+y²=a² –Уравнение окружности

Так как х и у в четной степени, кривая эллипса симметрична относительно координатных осей.

Фокусы всегда лежат на бОльшей оси.

Эксцентриситет равен расстоянию между фокусом и началом координат, Поделенному на длину большой полуосиоси. Всегда меньше единицы.

Директриса эллипса = 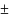отношение большой полуоси к экцентриситету.

Фокальные радиусы= сумма большой полуоси и произведения директрисы на эксцентриситет.

28.Гипербола.

Гипербота-геометрическое место точек, для каждой из которых абсолютная величина разности расстояний до двух данных точек-фокусов величина постоянная.Эта величина меньше,чем расстояние между фокусами.

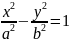-уравнение гиперболы.Если минус перед первым слагаемым, гипербола вертикальная.

Так как х и у в четной степени, кривая симметрична относительно осей.

Эксцентриситет равен отношению расстояний между началом координат и фокусок к длине действительной полуоси.Всегда больше единицы.

Директриса есть отношение действительной полуоси к эксцентриситету.