
- •Центральный экономико-математический институт ран Государственный академический университет гуманитарных наук
- •Числовая последовательность.
- •1. Предел числовой последовательности.
- •2. Теоремы о пределах.
- •3. Бесконечно малые величины (или последовательности).
- •4. Арифметические свойства пределов числовых последовательностей.
- •4. Предельный переход в равенствах и неравенствах
- •5. Неопределенные выражения.
- •Неопределенность вида .
- •Неопределенность вида .
- •6. Классификация бесконечно малых величин.
- •7. Классификация бесконечно больших величин.
Центральный экономико-математический институт ран Государственный академический университет гуманитарных наук
Макарчук Н.И.
Учебное пособие по курсу «Математический анализ»
2012
Некоторые понятие из теории множеств. Вещественные числа.
Понятие множества принадлежит к числу
первичных, не определяемых через другие
(более простые) понятия. Под множеством
понимается конечная или бесконечная
совокупность (набор) некоторых объектов,
объединенных одним свойством. Объекты,
которые образуют множество, называются
элементами (или точками) этого
множества. Множество обозначается
прописными буквами, а их элементы
- строчными буквами. Если а
элемент множества А, то используется
запись а![]() А,
если элемент b не
является элементом множества А,
то используется запись b
А,
если элемент b не
является элементом множества А,
то используется запись b
![]() А.
Множество, не содержащее ни одного
элемента, называется пустым множеством
и обозначается символом
А.
Множество, не содержащее ни одного
элемента, называется пустым множеством
и обозначается символом
![]()
![]() .
.
Если множество B
состоит из части множества А или
совпадает с ним, то В называют подмножеством
множества А и обозначают В![]() А.
Объединением двух множеств А и В
называется множество С, состоящее из
всех элементов, принадлежащих хотя бы
одному из данных множеств, т.е. С=А
А.
Объединением двух множеств А и В
называется множество С, состоящее из
всех элементов, принадлежащих хотя бы
одному из данных множеств, т.е. С=А![]() В.
Два множества называются равными,
если они состоят из одних и тех же
элементов. Пересечением двух множеств
А и В называется множество D, состоящее
из всех элементов, одновременно
принадлежащих каждому из данных множеств,
т.е. D =А
В.
Два множества называются равными,
если они состоят из одних и тех же
элементов. Пересечением двух множеств
А и В называется множество D, состоящее
из всех элементов, одновременно
принадлежащих каждому из данных множеств,
т.е. D =А![]() В.
Разностью двух множеств А и В
называется множество F,
состоящее элементов множества А, которые
не принадлежат множеству В, Обозначается
F=А\В, отсюда А\А=
.
Дополнением множества В (В
А)
называется множество Е, состоящее из
всех элементов множества А, не принадлежащих
множеству В. Отрицанием множества
А называется множество, не содержащее
ни одного элемента множества А,
обозначается оно
В.
Разностью двух множеств А и В
называется множество F,
состоящее элементов множества А, которые
не принадлежат множеству В, Обозначается
F=А\В, отсюда А\А=
.
Дополнением множества В (В
А)
называется множество Е, состоящее из
всех элементов множества А, не принадлежащих
множеству В. Отрицанием множества
А называется множество, не содержащее
ни одного элемента множества А,
обозначается оно
![]() ,
отсюда А
=
.
,
отсюда А
=
.
В алгебре множеств А В можно записать в виде АВ, А В=А+В.
Множества, элементами которых являются
вещественные, или действительные числа,
называются числовыми. Множество
вещественных чисел бесконечно. Оно
состоит из рациональных и иррациональных
чисел. Рациональным числом называют
число вида
![]() ,
где p и q целые числа. Всякое число, не
являющееся рациональным, называют
иррациональным. Рациональное число
либо целое, либо представляет собой
целую или периодическую бесконечную
десятичную дробь. Например, 7 – целое
число,
,
где p и q целые числа. Всякое число, не
являющееся рациональным, называют
иррациональным. Рациональное число
либо целое, либо представляет собой
целую или периодическую бесконечную
десятичную дробь. Например, 7 – целое
число,
![]() =0,2
–десятичная дробь,
=0,2
–десятичная дробь,
![]() =0,
3333…=0,3(3) - периодическую бесконечную
десятичную дробь.
=0,
3333…=0,3(3) - периодическую бесконечную
десятичную дробь.
Иррациональное число представляет
собой бесконечную непериодическую
десятичную дробь. Например,
![]() =
1,41421356…, число
=
1,41421356…, число
![]() =3,14159265….
=3,14159265….
Из школьного курса алгебры известны числовые множества и их обозначения:
R- множество действительных чисел,
Q- множество рациональных чисел,
I- множество иррациональных чисел,
Z- множество целых чисел (положительных, отрицательных и ноль),
N- множество натуральных чисел (1,2,3,…).
Очевидно, N Z Q R, I R, R=Q I, Q I= - пустое множество.
Для любой пары вещественных чисел а и в определены числа а+в и ав единственным образом, которые называются соответственно суммой и произведением.
Для любых чисел а,в,с имеют место следующие свойства.
1. Переместительное свойство: а+в=в+а; ав=ва.
2. Сочетательное свойство: (а+в)+с=а+(в+с); (ав) с=а (вс).
3. Распределительное свойство: (а+в)с=ас+вс.
4. Существует единственное число 0 (ноль), такое, что а+0=а для любого а.
5. Для любого числа а существует такое число (-а), что а+(-а)=0.
6.Существует единственное число 1![]() 0,
такое, что для любого числа а имеет
место а
0,
такое, что для любого числа а имеет
место а![]() =а.
=а.
7. Для любого числа а![]() существует такое число существует такое
число а
существует такое число существует такое
число а![]() ,
что
,
что
![]() а
=1.
Число а
обозначается
также символом
а
=1.
Число а
обозначается
также символом
![]() .
.
Числовая ось и множества на ней.
Между множеством вещественных чисел и множеством точек на прямой может быть установлено взаимно однозначное соответствие. Это дает возможность наглядно геометрически изобразить вещественные числа на числовой оси. Рациональные и иррациональные числа занимают всю числовую ось.
Выберем на прямой точку О – начало отсчета, укажем направление отсчета (обычно слева направо) и единицу измерения (масштаб). Эти три действия полностью определяют числовую ось. На ней вещественные числа изображаются в виде точек. На этой оси возьмем произвольную точку М, поставим ей в соответствие число x, равное по величине длине отрезка ОМ, со знаком «+», если точка М справа от точки О, со знаком «-» , если – слева от точки О. Число x называется координатой точки М. Справедливо и обратное утверждение : каждому вещественному числу x соответствует определенная точка на числовой (координатной) оси, координата которой равна x.
Взаимно однозначное соответствие между множествами.
Определение. Пусть даны два множества (конечные или бесконечные).
Если между элементами этих множеств
можно установить такое соответствие,
при котором каждому элементу одного
множества соответствует один и только
один элемент другого множества и обратно,
каждому элементу второго множества
соответствует один и только один элемент
первого множества, то говорят, что между
элементами этих множеств установлено
взаимно однозначное соответствие
(ВОС).
![]()
Пример 1.Даны множества А и В,
состоящие из конечного числа элементов.
Тогда ВОС устанавливается, если![]() и число элементов множества А= числу
элементов множества В.
и число элементов множества А= числу
элементов множества В.
Не ВОС, т.к.
![]()
![]() Нельзя установить
ВОС.
Нельзя установить
ВОС.
стрелки с
![]()
![]() т.к. одной точке множ. В
т.к. одной точке множ. В
одним концом А С А В соответствуют две точки
ВОС А В множества А
Пример 2. Множество А – множество всех целых положительных чисел (1, 2, 3, 4, …), В – множество всех целых отрицательных чисел (-1, -2, -3, -4, …).
Ответ: есть ВОС.
Пример 3. Может ли множество быть во ВОС со своим подмножеством?
Ответ: конечное – нет,
бесконечное – да. Пример: А-множество всех целых положительных чисел, В-множество всех четных положительных чисел, 1 2 3 4 … n …
2 4 6 8 … 2n …
П
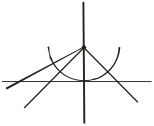
![]() ,
),
,
),
множество В – полуокружность с центром
в точке (0,1), радиус = 1.
Ответ: ВОС.
П
1
B
A
2
0 ример
5. Множество А –
ример
5. Множество А –
![]() ,
,
множество В – вся прямая ось (- , ).
y=tgx
Ответ: ВОС.
Пример 6. Множество А –
![]() ,
,
множество В –
![]() .
.
y=2x
Ответ: ВОС.
Определение. Два множества называются количественно эквивалентными (или просто эквивалентными) если между ними можно установит ВОС, пишут A~B.
Относительно двух эквивалентных множеств говорят, что они имеют одинаковую мощность (или равномощны).
Примеры 4, 5, 6 показывают, что полуокружность и прямая равномощны, все отрезки имеют одинаковую мощность и отрезки и вся прямая также равномощны.
Если А эквивалентно В, то пишут А![]() В.
Очевидно выполнены свойства.
В.
Очевидно выполнены свойства.
Тождественность: А А.
Транзитивность : если А В, В С, А С.
Симметрия : если А В, то В А.
Определение. Про любое множество, эквивалентное отрезку [0,1] говорят, что оно имеет мощность континуума.
Доказать, что любой отрезок [a,b], прямая (- , ) и полуокружность имеют мощность континуума (см.примеры 4, 5, 6).
Определение. Счетным множеством называется любое множество, эквивалентное множеству всех целых положительных чисел {1,2,3,…}. Иначе говоря, множество счетно, если все элементы можно пронумеровать:а1, а2,….
Свойства счетных множеств.
Объединение счетных множеств снова счетное множество: А1 А2.
Объединение конечного числа счетных множеств счетно: А1 А2 … Аn. А1 А2 .
Объединение счетного числа счетных множеств счетно:
 .
.
Все эти свойства нужно доказать.
Док-во 1 свойства. Пусть множество А={ а1, а2,…}, множества В= {b1, b2,…}.
Множество А В={ а1, b1, а2, b2,…}, пронумеруем элементы этого множества – получим счетное множество.
Для доказательства свойств счетных множеств удобно расположить элементы каждого множества Аk в последовательность {аnk}, к=1,2,3,…, т.е. в виде матрицы
множество А1 : а11 а12 а13 а14 ...
множество А2: а21 а22 а23 а24 ...
множество А3 : а31 а32 а33 а34 …
множество А4: а41 а42 а43 а44 …
и т.д.
Элементы объединения множеств рассматривать в виде множества {а11, а21, а12, а31, а22, а13 , а34 , а14, …}.
Имеют место следующие утверждения:
- любое подмножество счетного множества либо пусто, либо конечно, либо счетно;
- множество, эквивалентное счетному множеству, счетно; (док-во от противного)
- множество, эквивалентное несчетному множеству, несчетно;
- множества N, Z, Z0 (положительных целых чисел) – счетны;
- множество Q (множество рациональных чисел) – счетно;
- множества I (иррациональных чисел) и R (вещественных чисел) – несчетны;
- множество точек отрезка [0, 1] несчетно (нельзя пронумеровать);
- в любом интервале (a,b) числовой прямой содержится бесконечно много рациональных и иррациональных чисел;
- рациональные и иррациональные числа полностью «заполняют» числовую прямую.
Верхняя и нижняя грани множества вещественных чисел.
Определение. Множество вещественных
чисел Х={х} называется ограниченным
сверху (снизу), если существует такое
вещественное число М (число m), что каждый
элемент х множества Х удовлетворяет
неравенству х![]() М
(х
М
(х![]() m).
При этом число М (число m) называют
верхней гранью ( нижней гранью) множества
Х.
m).
При этом число М (число m) называют
верхней гранью ( нижней гранью) множества
Х.
Множество, ограниченное и сверху, и снизу называют ограниченным множеством.
Понятно, что любое ограниченное сверху множество имеет бесконечно много верхних граней, т.к. если М – верхняя грань множества {х}, то любое вещественное число М1 М, также является верхней гранью множества {х}.
Аналогичное замечание можно сделать относительно нижней грани m ограниченного снизу множества {х}. Возникает вопрос о существовании наименьшей из верхних граней ограниченного сверху множества и наибольшей из нижних граней ограниченного снизу множества.
Определение.
Наименьшая из всех верхних граней
ограниченного сверху множества {х}
называется точной верхней гранью
этого множества и обозначается символом
![]() =sup
{x}.
=sup
{x}.
Наибольшей из нижних граней ограниченного
снизу множества {х} называется точной
нижней гранью этого множества и
обозначается символом
![]() =
inf {x}. Символы заимствованы
из латинского языка: supremum- наивысший,
infimum – наинизший
=
inf {x}. Символы заимствованы
из латинского языка: supremum- наивысший,
infimum – наинизший
Или: число (число ) называется точной верхней гранью (точной нижней гранью)
Ограниченного сверху (снизу) множества
{х}, если выполнены следующие два
требования: 1). каждый элемент множества
{х} удовлетворяет неравенству х
(х
).
2). Каково бы ни было вещественное
число
![]() ,
меньшее
(большее
)
,
меньшее
(большее
)
найдется хотя бы один элемент множества {х}, удовлетворяющий неравенству х> (х< ). Второе условие говорит о том, что грань является наименьшей (наибольшей) и уменьшить (увеличить) её нельзя.
Существование у любого ограниченного сверху (снизу) множества точной верхней (точной нижней) грани не является очевидным. Ниже приводится теорема о существовании таких граней (без доказательства).
ТЕОРЕМА. Если множество Х={х} содержит хотя бы один элемент и ограничено сверху (снизу), то оно имеет точную верхнюю (нижнюю) грань.
Некоторые конкретные множества вещественных чисел
Обозначив множество вещественных чисел символом Х={х}, где х - точка (элемент) этого множества, будем говорить, что точка х1 множества {х} отлична от точки х2 этого множества , если вещественные числа х1 и х2 не равны друг другу. При этом, если х1> х2 (или х1< х2), то будем говорить, что точка х1 лежит правее точки х2 (левее х2).
Множество вещественных чисел Х={х}, удовлетворяющее неравенству
 , где а <b , будем
называть сегментом или отрезком
и обозначать [a,b],
точки a и b
называются граничными точками или
концами сегмента, а любое число х
, удовлетворяющее
, где а <b , будем
называть сегментом или отрезком
и обозначать [a,b],
точки a и b
называются граничными точками или
концами сегмента, а любое число х
, удовлетворяющее
 x<b,
внутренней точкой сегмента.
x<b,
внутренней точкой сегмента.Интервал, обозначается (a,b) – это множество всех вещественных чисел х, удовлетворяющих неравенствам x < b.
Полуинтервал (полусегмент), обозначается (а, b] или [а, b ) – это множество всех вещественных чисел х , удовлетворяющих неравенствам x b (или
 x
< b).
x
< b).Окрестность точки с – это любой интервал, содержащий точку с.
 -
окрестность точки с – это интервал
( c–
,c+
), где
>0.
-
окрестность точки с – это интервал
( c–
,c+
), где
>0.Множество всех вещественных чисел будем называть числовой (бесконечной) прямой и обозначать символом (- , ),
Множество всех вещественных чисел, удовлетворяющих неравенству х а (или х а) будем называть полупрямой и обозначать [а, ) или (- , a].
Множество всех вещественных чисел, удовлетворяющих неравенству х>а или
(х<а) будем называть открытой полупрямой и обозначать (а, ) или (- , a).
Полезные определения.
Множество А замкнуто, если каждая граничная точка А принадлежит А.
Точка называется внутренней точкой множества А, если она имеет окрестность такую, что эта окрестность принадлежит А.
Множество А открыто, если каждая точка А является внутренней точкой множества А.
Множество А открыто, если его дополнение замкнуто.
Абсолютная величина числа и её свойства.
Определение. Абсолютной величиной (или модулем) числа х называют само число х, если х неотрицательно, и противоположное число –х, если х отрицательно., т.е.
|x|=
х, при х![]() ,
|x|=
,
|x|=
![]() ,
при х<0
,
при х<0
Свойства:
1. |x| 0
2. |x|=|-x|
3. -|x|![]() |x|
|x|
4. Неравенства |x|
![]() и -а
а
равносильны при а>0.
и -а
а
равносильны при а>0.
5. Для любых двух чисел х и у справедливы неравенства:
|x+у| |x|+|у| |x-у| |x|+|у|
|x-у| |x|-|у| |x+у| |x|-|у|
|x![]() |=
|=![]()
![]()
![]() =
=![]() ,
(y
0).
,
(y
0).
Упражнения.
Определение ограниченного множества, ограниченного сверху (снизу) множества.
Ограничен ли натуральный ряд {1,2,3,…} сверху, снизу?
Что можно сказать об ограниченности множества правильных дробей?
Есть ли у множества правильных дробей точные верхняя и нижняя грани? Если есть, то какие?
Что можно сказать об ограниченности множества положительных правильных дробей?
Определение замкнутого множества. Пример. Определение внутренней точки множества. Какое множество называется открытым. Пример.
Какое множество называется счетным. Пример счетного и несчетного множества.
Найти нижнюю и верхнюю грани функции
 на
множестве
на
множестве
 .
.Определение взаимно однозначного соответствия между множествами. Примеры.
Найти нижнюю и верхнюю грани функции
 на
множестве
.
на
множестве
.Определение верхней и нижней грани множества вещественных чисел.
Найти нижнюю и верхнюю грани функции
 на
множестве
на
множестве
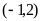 .
.Найти нижнюю и верхнюю грани функции
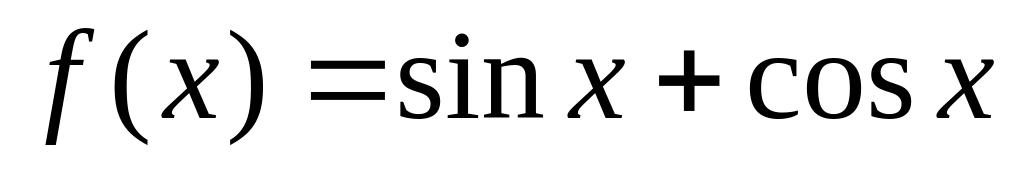 на
множестве
на
множестве
 .
.Что обозначает |х-а| (рассмотреть графическое изображение при х а и х>а)?
Какое множество представлено интервалом (а-
 )
?
)
?Определение верхней грани множества и определение точной верхней грани множества вещественных чисел. Привести пример.
Теорема о существовании точной верхней (нижней) грани у ограниченного сверху (снизу) числового множества.
Привести пример числовых множеств X, у которых :а) sup X X;
б) sup X X;
19. Привести пример числовых множеств X, у которых : а) inf X X;
б) inf X X;
