1.Определение матрицы. Прямоугольные и квадратные матрицы. Транспонированная матрица. Вектор-строка, вектор-столбец.

Матрицей называется таблица содержащая m строк и n столбцов, содержащая некоторые элементы

. aij- элемент матрицы, который находится в i-ой строке и j-м столбце.

Квадратная матрица - это матрица с равным числом столбцов и строк. Прямоугольная матрица - это матрица, в которой число строк не равно числу столбцов.

Транспонированная матрица получается в результате замены местами столбцов и строк матрицы. Т.е. вместо строк матрицы записываем столбцы матрицы, в результате чего размерность матрицы изменится с n x m на m x n.

Вектор-строка и вектор-столбец:

Матрица размера m*1 называется вектор-столбцом. Матрица размера 1*n называется вектор-строкой.

2.Действия над матрицами. Сумма двух матриц. Произведение числа 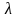на матрицу.

Сумма, произведение на число, произведение матриц.

Суммой двух матриц является матрица, каждый элемент которой равен сумме соответствующих элементов данных матриц. Складывать можно только матрица одинаковой размерности.

Сложение матриц подчиняется переместительному и сочетательному закону.

Умножение матрицы на число

Чтобы умножить матрицу на число следует каждый элемент матрицы умножить на это число.

3. Произведение матриц.

Элемент матрицы-произведения, находящегося на пересечении i-ой строки и j – столбца представляет собой сумму парных произведений элементов i- строки первой матрицы на элементы j – столбца второй матрицы.

Матрицы перемножаются только в том случае, если количество столбцов первой матрицы равно количеству строк второй матрицы.

4.Нулевая матрица. Диагональная матрица. Единичная матрица, ее свойства.

Нулевая матрица - матрица, все элементы которой равны нулю.

Диагональная матрица - квадратная матрица, у которой все элементы, стоящие не на главной диагонали, равны нулю.

Единичная матрица - это диагональная матрица, у которой каждый элемент на главной диагонали равен единице.

Свойства: 1) Произведение любой матрицы и единичной матрицы(ЕМ) подходящего размера равно самой матрице: АЕ = ЕА = А

2) Квадратная матрица в нулевой степени дает ЕМ того же размера: А^0 = Е

3) При умножении матрицы на обратную ей тоже получается ЕМ: АА^-1 = Е

4) ЕМ получается при умножении ортогональной матрицы на ее на её транспонированную матрицу: АА^т = Е

5) Определитель единичной матрицы равен единице: det E = 1

5. Определители 1-го, 2-го, 3-го порядков. Миноры. Алгебраические дополнения.

Определитель 1го порядка равен тому единственному элементу, из которого состоит соответствующая матрица.

Определитель 2го порядка равен произведению элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной диагонали.

Вычисление определителя 3го порядка сводится к вычислению определителей второго порядка, получается, что определитель n - го порядка мы найдем через определители (n -1) - го порядка.

Минором Мij элемента aij матрицы n-го порядка, полученный из матриц

А вычеркиванием i-й строки и j-го столбца. При выписывании определителя (n-1)-го порядка, в исходном определителе элементы находящиеся под линиями в расчет не принимаются.

Алгебраическим дополнением элемента аij матрицы А называется число , где Мij – доп. Минор, определитель матрицы, получающейся из исходной матрицы А путем вычёркивания i -й строки и j -го столбца

6. Теорема о разложении определителя по элементам строки или столбца.

Определитель равен сумме произведению элементов любой строки или любого столбца на их алгебраические дополнения.

)

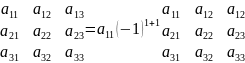
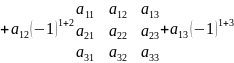
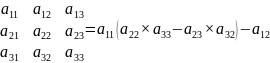
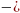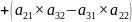
7.Транспонирование определителя. Теорема о транспонировании. Теорема об общем множителе строки(столбца) определителя. Определитель с нулевой строкой(столбцом).

При транспонировании определитель не изменяется.

Доказ. Если дан определитель det A

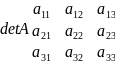
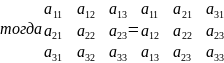
Для доказательства достаточно применить к определителям стоящим в левой и правой частях равенства формулу 2.и убедиться в равенстве полученных выражениях.

Теорема 3 об общем множителе строки(столбца)опред-ля.Общий множитель одного столбца или одной строки можно вынести за знак определителя.

Иначе или определитель умножается на число, то на это число умножаются все элементы какой нибудь одной строки(любой)или какого нибудь одного столбца(любого).

Определитель с нулевой строкой(столбцом).Определитель имеющий нулевую строку или нулевой столбез равен нулю.

Док-во.Нулевую строку можно представить как строку можно представить как строку с общим множителем ноль. Согласно тер.3. на ноль в этом случается умножается весь определитель.

8. Теорема о перестановке двух строк (столбцов) определителя. Признак нулевого определителя.

Т.5.Если в определителе поменять местами две любые строки или 2 любых столбца, знак определителя изменится на противоположный.

Признак нулевого определителя.Если определитель имеет две одинаковые строки или 2 одинаковых столбца, то он равен нулю.

Док-во.При замене двух одинаковых строк местами не меняется ничего, но по Т.5 знак определителя меняется на обратный.

Δ= - Δ => 2Δ=0 Δ=0

9. Теорема о представлении определителя в виде суммы определителей.

10.Теорема о тождественном преобразовании определителя.

Если к каждому элементу какой-нибудь строки или какому-нибудь столбцу прибавить числа пропорциональные соответствующим элементам другой строки и соответствующего столбца, то определитель от этого не изменится.

11.Ранг матрицы.

Рангом матрицы называется наивысший порядок минора матрицы отличного от нуля.

Все миноры 2 и 3 порядка данной матрицы будут равны нулю т.к элементы сток пропорциональны. Миноры 1 порядка (сами элементы матрицы не равны нулю) следовательно, данная матрица имеет ранг =1.

Минором данной матрицы называется определитель, составленный без перестановок из оставшихся элементов матрицы после вычеркивания из них нескольких строк и столбцов.

Миноров третьего порядка будет четыре, и они получаются после вычеркивания одного столбца и замены знака матрицы , знаком определителя. Миноров 10го порядка 12.Миноров 2-ого порядка 18.

Если матрица А квадратная порядка n, то ранг такой матрицы будет .Если , то матрица называется невырожденной. Если - выражденная.

Всякий отличный от нуля минор матрицы, порядок которого равен рангу матрицы называется базисным минором. Если каждый элемент матрицы равен нулю, то ранг такой матрицы по определению будет равен нулю. Подсчет ранга матрицы по определению требует грамостких расчетов, т.к перебор всех миноров в поиске базистого задача трудная, если размеры матрицы велики. Проще находить ранг матрицы при помощи элементарных преобразований.