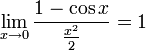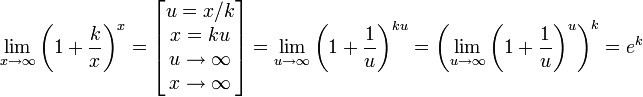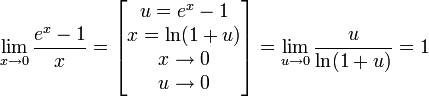8. Первый и второй замечательные пределы

Первый замечательный предел

Доказательство

Рассмотрим односторонние пределы   и   и докажем, что они равны 1.

Пусть  . Отложим этот угол на единичной окружности ( ).

Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке  . Точка H — проекция точки K на ось OX.

Очевидно, что:

 (1)

(где   — площадь сектора  )

(из  :  )

Подставляя в (1), получим:

Так как при  :

Умножаем на  :

Перейдём к пределу:

Найдём левый односторонний предел:

Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.

Следствия

• 

• 

• 

• 

Доказательства

[править]Второй замечательный предел

 или 

Доказательство второго замечательного предела:

Доказательство для натуральных значений

  Докажем вначале теорему для случая последовательности 

По формуле бинома Ньютона: 

Полагая  , получим:

       (1)

Из данного равенства (1) следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число   убывает, поэтому величины   возрастают. Поэтому последовательность   — возрастающая, при этом

      (2).

Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу, правая часть увеличится, получим неравенство

Усилим полученное неравенство, заменим 3,4,5, …, стоящие в знаменателях дробей, числом 2:

.

Сумму в скобке найдём по формуле суммы членов геометрической прогрессии:

.

Поэтому        (3).

Итак, последовательность ограничена сверху, при этом   выполняются неравенства (2) и (3):    .

Следовательно, на основании теоремы Вейерштрасса (критерий сходимости последовательности) последовательность   монотонно возрастает и ограниченна, значит имеет предел, обозначаемый буквой e. Т.е.   

   Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что  . Рассмотрим два случая:

1. Пусть  . Каждое значение x заключено между двумя положительными целыми числами:  , где   — это целая часть x.

Отсюда следует:  , поэтому

.

Если  , то  . Поэтому, согласно пределу  , имеем:

.

По признаку (о пределе промежуточной функции) существования пределов  .

2. Пусть  . Сделаем подстановку  , тогда

.

Из двух этих случаев вытекает, что   для вещественного x.    

Следствия

1. 

2. 

3. 

4. 

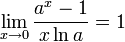5.  для  , 

6. 

Доказательства следствий

1. 

2. 

3. 

4. 

5. 

6. 

9. Бесконечно малые и бесконечно большие функции

Определение. Функция   называется бесконечно малой при  , если  .

Определение. Функция   называется бесконечно большой при  , если  .

Лемма. Если   при  , то   при  , если   при  , то   при   и  .

Например, функции   и   взаимнообратны. При   функция   является бесконечно малой, а   – бесконечно большой, если  .

Сформулируем основные теоремы о бесконечно малых.

Теорема. Алгебраическая сумма конечного числа бесконечно малых при   функций является бесконечно малой при   функцией.

Теорема. Произведение конечного числа бесконечно малых при   функций является бесконечно малой при   функцией.

Теорема. Произведение бесконечно малой при   функции на функцию, ограниченную в некоторой окрестности точки  , является бесконечно малой при   функцией.

Определение. Две бесконечно малые при   функции   и  называются эквивалентными при  , если  , т.е.   при  .

Определение. Две бесконечно малые при   функции   и   называются бесконечно малыми одинакового порядка, если  , где   и конечно.

Например, функции   и   при   являются бесконечно малыми одинакового порядка, так как  .

Определение. Бесконечно малая при   функция   называется функцией более высокого порядка по сравнению с функцией   при  , если  .

В этом случае пишут  .

Так, функция   является бесконечно малой более высокого порядка по сравнению с   при  , так как  .

10. Сравнение бесконечно малых функций

Пусть   б.м. функции  при  . Предположим, что существует предел их отношения и он равен l.

.

Тогда если:

1)   l=1, то функции   и   называются эквивалентными б.м.;

2)   l - число, l¹0, то функции   и   называются б.м. одинакового порядка;

3)  l=0, то функция   называется б.м. более высокого порядка, чем  ;

4)  l= ±¥, то функция   называется б.м. более высокого порядка, чем  .

Пример 1.  ,   ,

,

 и   - эквивалентные б.м. функции.

Пример 2.   =х³,

=х,

,

,

 - б.м. функция более высокого порядка, чем  .

11. Непрерывность функции. Точки разрыва

Непрерывные функции 

     Определение 1: Функция f(x) называется непрерывной функцией в точке A, если существует предел данной функции при аргументе стремящимся к A и он равен f(a), т.е.  .

     Критерий непрерывности:

Другими словами, для любого сколь угодно малого числа эпсилон, существует такое число дельта, зависящее от эпсилон, что из того, что для любых иксов удовлетворяющих неравенству следует, что отличия значений функции в данных точках будет сколь угодно мало.

     Критерий непрерывности функции в точке:

      Функция будет непрерывна в точке A тогда и только тогда, когда она будет непрерывна в точке A и справа и слева, т.е чтобы в точке A существовали два односторонних предела, они были равны между собой и равнялись значению функции в точке A.

      Определение 2: Функция непрерывна на множестве, если она непрерывна во всех точках этого множества.

 

Свойства непрерывных функций. Точки разрыва функций

a) Свойства непрерывных функций 

     1) Если функция непрерывна в точке A, то она ограничена в некоторой окрестности точки A. Данное свойство следует из локальной ограниченности функции, имеющей конечный предел.

     2) Теорема о стабилизации знаков

     Пусть функция непрерывна в точке A, причем f(A) отлично от нуля, тогда существует окрестность точки A такая, что знак функции в окрестности будет совпадать со знаком функции в точке A.

     3) Пусть функции f и g непрерывны в точке A, тогда:

• n*f + m*g также будет непрерывной функцией в точке A, где n,m - константы.

• f*g, f/g (при g(A) отличном от нуля) будут непрерывными функциями

 

b) Точки разрыва функции

    Определение 3: Точку В из области определения функции будем называть точкой разрыва функции, если функция не является непрерывной в точке B.

 1) Точка разрыва функции называется точкой неопределенности, если не существует правого либо левого одностороннего предела.

 2) Если существует оба односторонних предела, но по крайней мере один из них не конечен , то точка разрыва называется точкой бесконечного скачка

 3) Если существует оба односторонних предела, но они не равны между собой , то точка разрыва называется точкой конечного скачка

 4) Если существует оба односторонних предела и они не равны между собой, но не равны значению функции в данной точке, то точка разрыва называется точкой устраненного разрыва

     Разрывы из пунктов 1) и 2) называются разрывами второго рода, а из пунктов 3) и 4)разрывами первого рода.

12. Производная функции. Геометрический смысл

Геометрический смысл производной. Производная в точке x ₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

Рассмотрим график функции y = f ( x ):

Из рис.1 видно, что для любых двух точек A и B графика функции:  xf(x0+ x)−f(x0)=tg , где   - угол наклона секущей AB.  Таким образом, разностное отношение равно угловому коэффициенту секущей.  Если зафиксировать точку A и двигать по направлению к ней точку B, то  x неограниченно уменьшается и приближается к 0, а секущая АВприближается к касательной АС.  Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует:

производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.

В этом и состоит геометрический смысл производной.

13. Таблица производных

14. Правила дифференцирования

См таблицу.

15. Производная параметрической и неявной функции

Несомненно, в нашем сознании образ функции ассоциируется с равенством   и соответствующей ему линией – графиком функции. Например,   - функциональная зависимость, графиком которой является квадратичная парабола с вершиной в начале координат и направленными вверх ветвями;   - функция синуса, известная своими волнами.

В этих примерах в левой части равенства находится y, а в правой части – выражение, зависящее от аргумента x. Другими словами, имеем уравнение, разрешенное относительно y. Представление функциональной зависимости в виде такого выражения называется явным заданием функции (или функцией в явном виде). И этот тип задания функции является для нас наиболее привычным. В большинстве примеров и задач нам предстают именно явные функции. Про дифференцирование функций одной переменной, заданных в явном виде, мы уже в деталях поговорили.

Однако, функция подразумевает соответствие между множеством значений величины x и множеством значений y, причем это соответствие НЕ обязательно устанавливается какой-либо формулой или аналитическим выражением. То есть, существует множество способов задания функции помимо привычного  .

В данной статье мы рассмотрим неявные функции и способы нахождения их производных. В качестве примеров функций, заданных неявно, можно привести   или  .

Как Вы заметили, неявная функция определяется соотношением  . Но не все такие соотношения между x и y задают функцию. Например, ни одна пара действительных чисел x иy не удовлетворяет равенству  , следовательно, это соотношение неявную функцию не задает.

 может неявно определять закон соответствия между величинами x и y, причем каждому значению аргумента x может соответствовать как одно (в этом случае имеем однозначную функцию) так и несколько значений функции (в этом случае функцию называют многозначной). К примеру, значению x = 1 соответствует два действительных значения y = 2 иy = -2 неявно заданной функции  .

Неявную функцию   привести к явному виду далеко не всегда возможно, иначе не пришлось бы дифференцировать сами неявные функции. Например,   - не преобразовывается к явному виду, а   - преобразовывается.

Теперь к делу.

Чтобы найти производную неявно заданной функции, необходимо продифференцировать обе части равенства   по аргументу x, считая y – функцией от x, и после этого выразить  .

Дифференцирование выражений, содержащих x и y(x), проводится с использованием правил дифференцирования и правила нахождения производной сложной функции. Давайте сразу подробно разберем несколько примеров, чтобы дальше не было вопросов.