1. Определители и их св-ва

Любая квадратная матрица имеет некую числовую характеристику называемой определителем матрицы, который вычисляется по формуле.

Если определитель матрицы равен нулю, то матрица называется вырожденной и наоборот.

Определитель обозначается |A| или det A

Свойства определителя

1. Определитель меняет свое значение при транспонировании

2. Определитель меняет знак на противоположный, если поменять местами любые две строки или любые два столбца.

3. Определитель равен нулю, если он содержит нулевую строку или столбец.

4. Определитель равен нулю, если он содержит две одинаковых строки или столбца.

5. Определитель равен нулю, если он содержит две пропорциональные строки или столбца.

6. Общий множитель строки или столбца можно выносить за знак определителя.

7. При умножении определителя на число, на него умножается только одна строка ( в отличии от матриц)

8. Свойство Гаусса: Определитель не изменит своего значения, если к каждому элементу какой-либо или столбца прибавить соответствующие элементы другой строки или столбца, умноженные на одно и то же число, отличное от нуля.

2. Матрицы и действия с ними

Матрицей называется прямоугольная таблица, состоящая из m-строк и n-столбцов, заключённая в круглые скобки.

Виды матриц:

1. m не равн. n прямоугольная матрица

2. m=n квадратная матрица

3. m=1;n не равн 1 матрица-строка

4. m не равн 1;n=1 матрица-столбец

5. m=0;n=0 нулевая матрица

6. Единичная матрица

Действия с матрицами:

1. Умножение числа на матрицу

Для того, чтобы умножить число на матрицу, нужно умножить на это число каждый элемент матрицы

2. Сложение матриц

Сложение двух матриц одинаковой размерности А+В, называется матрица той же размерности С, элементы которой равны сумме соответствующих элементов сходных матрице

(аналогична разность двух матриц)

3. Транспонирование матриц

Транспонировать матрицу это значит – заменить строки с одинаковыми столбцами

4. Равенство матриц

Две матрицы равны, если 1) размерности этих матриц одинаковы; 2) соответствующие элементы равны между собой

5. Перемножение матриц

Произведением матрицы А на матрицу В, называется С.

Элементы матрицы С ,получаются как сумма соответствующих элементов строки матрицы А на столбец матрицы В (Строка на столбец)

1. Количество столбцов 1-й матрицы должно совпадать с количеством строк второй

2. Размерность матрицы С определяется количеством строк первой и количеством столбцов второй матрицы.

3. Обратные матрицы. Решение матричных уравнений

Для любого числа А существует обратное чисто А (в минус первой степени) , такое, что их произведение равняется 1

Матрица А в степени -1 называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как с лева так и справа, получается единичная матрица

Условием существования матрицы в степени -1 является определитель не равный нулю

Нахождение обратной матрицы:

А^(-1)= 1/▲А * А~

1. Найти определитель матрицы А

2. Найти A~

1. Транспонировать матрицу А

2. Вычислить алгебраические дополнения всех элементов полученной матрицы

3. Составить из них матрицу А~

3. Находим обратную матрицу

4. Системы линейных уравнений, формулы Крамера

Решение систем линейных уравнений по формуле Крамера.

Пусть дана система n-линейных уравнений с n-неизвестными х₁, х₂,..., х _n:

а₁₁х₁+а₁₂х₂+...+а_1nх_n=b₁,

(1)

а₂₁х₁+а₂₂х₂+...+а_2nх_n=b₂,

... .... .... ... .... ... ... ... ....

а_n1х₁+а_n2х₂+...+а_nnх_n=b_n.

Матрица, составленная из коэффициентов при неизвестных, и её определитель называются соответственно матрицей системы (1) и определителем этой системы.

Пусть А_ij (i, j =1, 2,...,n)– алгебраические дополнения элементов определителя . Преобразуем систему (1) так, чтобы каждое из её уравнений содержало только одно неизвестное. Для этого умножим первое уравнение системы на А₁₁, второе – на А₂₁,..., n-е – на А_n1 и сложим их; затем умножим уравнения системы соответственно на А₂₁, А₂₂, ..., А_n2 и сложим их, и т.д., наконец, умножим уравнения системы соответственно на А_n1, А_n2, ..., А_nn и опять сложим. Получим новую систему уравнений:

(2)

х₁= b₁А₁₁+ b₂ А₂₁+...+ b_n А_n1,

х₂= b₁А₁₂+ b₂ А₂₂+...+ b_n А_n2,

... ... ... ... ... ... ... ... ... ... ... ... ...,

х_n= b₁А_1n+ b₂ А_2n+...+ b_n А_nn.

Правые части уравнения системы (2) обозначим соответственно символами ₁, ₂, ..., _n, где

Тогда система уравнений (2)примет вид:

(4)

х₁=₁,

х₂=_2,

... ... ... ...,

х_n=_n.

Если , то из этих уравнений находим

5. Решение систем линейных уравнений методом Жордана-Гаусса

Алгоритм метода Жордана-Гаусса

Алгоритм решения систем уравнений методом Жордана-Гаусса состоит из ряда однотипных шагов, на каждом из которых производятся действия в следующем порядке:

1. Проверяется, не является ли система несовместной. Если система содержит противоречивое уравнение, то она несовместна.

2. Проверяется возможность сокращения числа уравнений. Если в системе содержится тривиальное уравнение, его вычеркивают.

3. Если система уравнений является разрешенной, то записывают общее решение системы и если необходимо — частные решения.

4. Если система не является разрешенной, то в уравнении, не содержащем разрешенной неизвестной, выбирают разрешающий элемент и производят преобразование Жордана с этим элементом.

5. Далее заново переходят к пункту 1

Пример 3 Решить систему уравнений методом Жордана-Гаусса.

Найти: два общих и два соответствующих базисных решения

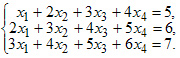
Решение:

Вычисления приведены в нижеследующей таблице:

Справа от таблицы изображены действия над уравнениями. Стрелками показано к какому уравнению прибавляется уравнение с разрешающим элементом, умноженное на подходящий множитель.

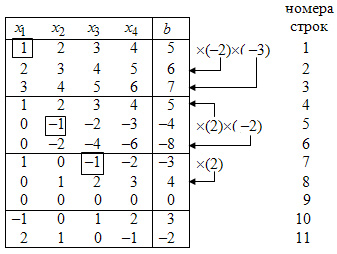
В первых трех строках таблицы помещены коэффициенты при неизвестных и правые части исходной системы. Результаты первого преобразования Жордана с разрешающим элементом равным единице приведены в строках 4, 5, 6. Результаты второго преобразования Жордана с разрешающим элементом равным (-1) приведены в строках 7, 8, 9. Так как третье уравнение является тривиальным, то его можно не учитывать.

Равносильная система с разрешенными неизвестными   и   имеет вид:

Теперь можем записать Общее решение:

Приравниваем свободные переменные   и   нулю и получаем:  .

Базисное решение: 

Для того чтобы найти второе общее и соответствующее ему базисное решение, в полученной разрешенной системе в каком-либо уравнении необходимо выбрать какой-либо другой разрешающий элемент. (дело в том, что линейное уравнение может содержать несколько общих и базисных решений). Если разрешенная система уравнений, равносильная исходной системе содержит   неизвестных и   уравнений, то число общих и соответствующих базисных решений исходной системы равно числу сочетаний   и  . Количество сочетаний можно вычислить по формуле:

В нашем случае выбран разрешающий элемент (-1) в первом уравнении при   (строка 7). Далее производим преобразование Жордана. Получаем новую разрешенную систему (строки 10,11) c новыми разрешенными неизвестными   и  :

Записываем второе общее решение:

И соответствующее ему базисное решение: