26. Масса и импульс фотона. Эффект Комптона

Согласно гипотезе световых квантов Эйнштейна, свет испускается, поглощается и распространяется дискретными порциями (квантами), названными фотонами. Энергия фотона . Его масса находится из закона взаимосвязи массы и энергии

Фотон движется со скоростью света c = 3·10⁸ м/с Подставим это значение скорости в выражение тогда получим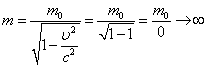

Фотон — элементарная частица, которая всегда (в любой среде!) движется со скоростью света с и имеет массу покоя, равную нулю. Следовательно, масса фотона отличается от массы таких элементарных частиц, как электрон, протон и нейтрон, которые обладают отличной от нуля массой покоя и могут находиться в состоянии покоя.

Импульс фотона р_ получим, если в общей формуле теории относительности положим массу покоя фотона m_0 = 0:

p=mc, (205.2)

Из приведенных рассуждений следует, что фотон, как и любая другая частица, характеризуется энергией, массой и импульсом. Выражения (205.1), (205.2) и (200.2) связывают корпускулярные характеристики фотона — массу, импульс и энергию — с волновой характеристикой света — его частотой v.

Опыты показали, что разность /_\ =— не зависит от длины волны  падающего излучения и природы рассеивающего вещества, а определяется только углом рассеяния в:

(206.1)

где  — длина волны рассеянного излучения, l_C - комптоновская длина волны (при рассеянии фотона на электроне l_C =2,426 пм).

Эффектом Комитета называется упругое рассеяние коротковолнового электромагнитного излучения (рентгеновского и -излучений) на свободных (или слабосвязанных) электронах вещества, сопровождающееся увеличением длины волны. Этот эффект не укладывается в рамки волновой теории, согласно которой длина волны при рассеянии изменяться не должна: под действием периодического поля световой волны электрон колеблется с частотой поля и поэтому излучает рассеянные волны той же частоты.

Объяснение эффекта Комптона дано на основе квантовых представлений о природе света. Если считать, как это делает квантовая теория, что излучение имеет корпускулярную природу, т. е. представляет собой поток фотонов, то эффект Комптона — результат упругого столкновения рентгеновских фотонов со свободными электронами вещества (для легких атомов электроны слабо связаны с ядрами атомов, поэтому их можно считать свободными). В процессе этого столкновения фотон передает электрону часть своих энергии и импульса в соответствии с законами их сохранения.

Рассмотрим упругое столкновение двух частиц (рис. 291) — налетающего фотона, обладающего импульсом р_g = hv/c и энергией _ = hv, с покоящимся свободным электроном (энергия покоя W₀ = m₀c²; m₀ — масса покоя электрона). Фотон, столкнувшись с электроном, передает ему часть своей энергии и импульса и изменяет направление движения (рассеивается). Уменьшение энергии фотона означает увеличение длины волны рассеянного излучения. При каждом столкновении выполняются законы со хранения энергии и импульса.

Согласно закону сохранения энергии,

(206.2)

а согласно закону сохранения импульса,

где W₀ = m₀c² —энергия электрона до столкновения, e_g = hv — энергия налетающего фотона, — энергия электрона после столкновения (используется релятивистская формула, так как скорость электрона отдачи в общем случае значительна), e_r=Av' — энергия рассеянного фотона. Подставив в выражение (206.2) значения величин и представив (206.3) в соответствии с рис. 291, получим

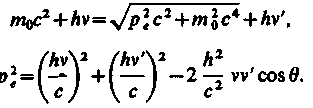(206.4) (206.5)

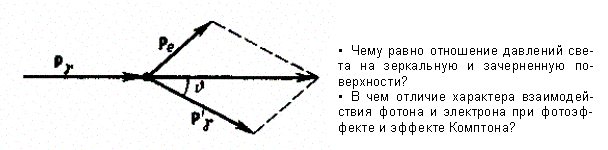
Рис. 291

Решая уравнения (206.4) и (206.5) совместно, получим

Поскольку v = c/, v'=c/l' и l = l'—l, получим

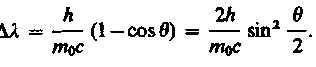
Выражение (206.6) есть не что иное, как полученная экспериментально Комптоном формула (206.1). Подстановка в нее значений h, m₀ и с дает комптоновскую длину волны электрона l_C = h/(m_Cс) = 2,426 им.

. При рассмотрении механизма рассеяния предполагалось, что фотон соударяется лишь со свободным электроном, фотон обменивается энергией и импульсом с атомом в целом. Так как масса атома по сравнению с массой электрона очень велика, то атому передается лишь ничтожная часть энергии фотона. Поэтому в данном случае длина волны l' рассеянного излучения практически не будет отличаться от длины волны l падающего излучения.

Как эффект Комптона, так и фотоэффект на основе квантовых представлении обусловлены взаимодействием фотонов с электронами. В первом случае фотон рассеивается, во втором — поглощается. Рассеяние происходит при взаимодействии фотона со свободным электроном, а фотоэффект — со связанными электронами. Можно показать что при столкновении фотона со свободным электроном не может произойти поглощения фотона, так как это находится в противоречии с законами сохранения импульса и энергии. Поэтому при взаимодействии фотонов со свободными электрона-ми может наблюдаться только их рассеяние, т. е. эффект Комптона.