Диф.Урав-ние теплопроводности. Краевые условия.

При выводе дифференциального уравнения теплопроводности считаем, что тело однородно и изотропно (то есть физические свойства тела не зависят от выбранного в нём направления), физические параметры λ, с(теплоемкость), и ρ (плотность) постоянны, внутренние источники теплоты равномерно распределены в теле. Под внутренними источниками теплоты понимаются тепловыделения. Внутренние источники теплоты характеризуются величиной qv — количеством теплоты, которое выделяется в единице объема в единицу времени.

В основу вывода положен закон сохранения энергии, согласно которому вся теплота, выделенная внутренними источниками dQвн и внесенная извне в элементарный объем путем теплопроводности dQm за время dτ, идет на изменение внутренней энергии вещества, содержащегося в этом объеме:

Выделим в теле элементарный параллелепипед с ребрами dx, dy, dz. Количество теплоты, которое проходит путем теплопроводности внутрь выделенного объема в направлении оси ОX через элементарную площадку dy·dz за время dτ:

После преобразования получим дифференциальное уравнение теплопроводности: ,где - коэффициент температуропроводности.

Д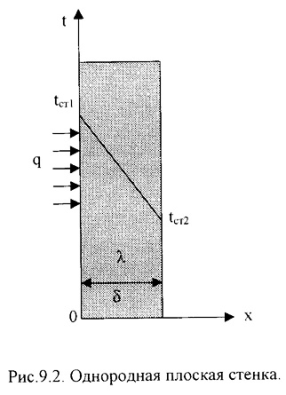 ифференциальное уравнение описывает в самом общем виде все без исключения задачи теплопроводности. Для решения конкретной задачи необходимо к дифференциальному уравнению присоединить математическое описание частных ее особенностей. Эти дополнительные данные, которые характеризуют конкретное единичное явление, называются краевыми условиями, или условиями однозначности.

Существуют различные условия однозначности: геометрические — характеризующие форму и размеры тела, в котором протекает процесс теплопроводности; физические — характеризующие физические свойства тела; временные — характеризующие распределение температуры тела в начальный момент времени; граничные — характеризующие взаимодействие тела с окружающей средой. Граничные условия в свою очередь бывают трех родов:

1) первого рода, задается распределение температуры на поверхности тела в функции времени;

2) второго рода, задается плотность теплового потока для всей поверхности тела в функции времени;

3) третьего рода, задаются температура окружающей среды tж и закон теплоотдачи между поверхностью тела и окружающей средой — закон Ньютона—Рихмана: ,получаем

Теплопроводность плоской однослойной и многослойной стенок.

1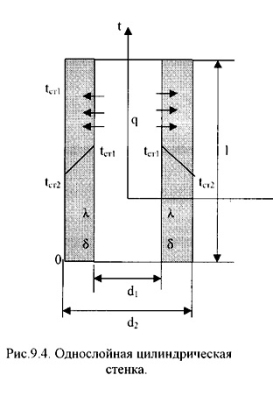 )Однородная плоская стенка (Рис.9.2.). Температуры поверхностей стенки –t_ст1 и t_ст2. Плотность теплового потока:

q = -λ∙ ∂t/∂n = - λ∙ ∂t/∂x = - λ∙ (t_cт2 - t_cт1)/(x_cт2 - x_cт1)∙ или q = λ∙ (t_cт2 - t_cт1)/(x_cт2 - x_cт1)∙t/x Тогда

q = λ/δ∙(t_ст1 – t_ст2) = λ/δ∙Δt,

Если R =δ/λ -термическое сопротивление теплопроводности стенки [(м²∙К)/Вт], то плотность теплового потока

q = (t_ст1 – t_ст2)/R .

Общее количество теплоты, которое передается через поверхность F за время τ определяется:

Q = q∙F∙τ = (t_ст1 – t_ст2)/R·F∙τ .

Температура тела в точке с координатой х находится по формуле:

t_x = t_ст1 – (t_ст1 – t_ст2)∙x/ δ .

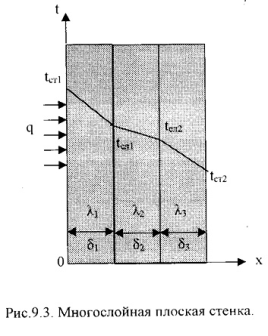
2).Многослойная плоская стенка. Рассмотрим 3-х слойную стенку (Рис.9.3). Температура наружных поверхностей стенокt_ст1 и t_ст2, коэффициенты теплопроводности слоевλ₁, λ₂, λ₃, толщина слоевδ₁, δ₂, δ₃. Плотности тепловых потокок через каждый слой стенки:

q = λ₁/δ₁∙(t_ст1 – t_сл1) , (9.18) q = λ₂/δ₂∙(t_сл1 – t_сл2) , q = λ₃/δ₃∙(t_сл2 – t_ст2) ,

Решая эти уравнения, относительно разности температур и складывая, получаем:

q = (t₁ – t₄)/(δ₁/λ₁ + δ₂/λ₂ + δ₃/λ₃) = (t_ст1 – t_ст4)/R_o ,

где: R_o = (δ₁/λ₁ + δ₂/λ₂ + δ₃/λ₃) – общее термическое сопротивление теплопроводности многослойной стенки. Температура слоев определяется по следующим формулам:

t_сл1 = t_ст1 – q∙(δ₁/λ₁). t_сл2 = t_сл1 – q·δ₂/λ₂).