28. Канонические уравнения метода сил для дважды статически неопределимой фермы запишутся:

где ₁₂ - перемещение по направлению Х₁ от действия X₂ = 1,

_2P - перемещение по направлению X₂ от действия внешней нагрузки.

Имея ввиду, что в элементах ферм возникают только продольные усилия, коэффициенты системы канонических уравнений определяются одним слагаемым формулы Мора:

,

учитывая, что жесткость стержней ферм по длине постоянна (EI_i = const) и постоянна продольная сила в пределах стержня = const:

; и т.д. ,

где n - число стержней в ферме.

Суммирование ведется по всем стержням фермы, в том числе и разрезанным!

- усилия во всех стержнях основной системы фермы от действия X₁ = 1;

N_pi- усилия во всех стержнях основной системы фермы от действия внешней нагрузки.

После того, как будут вычислены неизвестные X₁, X₂, X_k, усилия в стержнях заданной фермы определяются по формуле:

Правильность выполнения решения проверяют с помощью деформационной проверки:

Расчет ведут обычно в табличной форме:

Линии влияния усилий в стержнях статически неопределимых ферм

Поскольку усилия в стержнях статически неопределимых ферм выражаются через лишние неизвестные

,

то при расчете фермы на подвижную нагрузку необходимо вначале построить линии влияния лишних неизвестных.

Т.е. линия влияния усилия в произвольном стержне фермы получается путем суммирования линии влияния усилия в статически определимой основной системе фермы и линии влияния лишних неизвестных X_k, все значения которых умножаем на

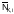
29 Статически неопределимые комбинированные системы

В строительной механике под комбинированными понимают системы состоящие из комбинации рамных элементов, работающих в основном на изгиб и шарнирно-стержневых элементов, работающих на растяжение или сжатие.

Рассчитывают комбинированные системы, как правило, методом сил (если речь идет о ручном счете).

Особенностью расчета является определение коэффициентов системы канонических уравнений метода сил:

I слагаемое относится к рамным элементам, II – к шарнирно-стержневым элементам.

Первое слагаемое обычно определяют путем перемножения эпюр (используя для этого правило Верещагина или формулу Симпсона).

Второе слагаемое, как для статически неопределимых ферм:

Основную систему метода сил выбираем, разрезая 3 элемента фермы:

Для определения коэффициентов рассмотрим единичные и грузовое состояния основной системы :

Определяем коэффициенты, решаем систему и находим X₁, X₂ ,X₃.

После чего:

.

31.Расчёт неразрезных балок методом перемещений.

Степень линейной подвижности неразрезной балки всегда равна нулю.

Степень угловой подвижности равна числу промежуточных опор, т.е. для неразрезных балок число неизвестных метода перемещений определяется =_; т.к. _=0.

И далее как в обычном методе перемещений

32. Расчёт неразрезных балок методом сил

Степень статической неопределимости неразрезной балки может быть определена по формуле Чебышева.

=C_ОП+2Ш₀-2D, но учитывая, что Ш₀=0, а D=1, частный вид формулы:

=C_ОП – 3

Исторически первоначально основную систему метода сил выбирали, отбрасывая «лишние» опорные связи:

Единичные эпюры при таком выборе основной системы распространяются на всю длину балки и ни один из единичных коэффициентов системы канонических уравнений не равен нулю.

В процессе практических расчетов убедились, что более рационально основную систему выбирать, вводя в промежуточные опорные сечения перерезывающие шарниры. В качестве неизвестных, при таком выборе основной системы, выступают опорные моменты. Единичные эпюры распространяются только на два соседних пролета и канонические уравнения метода сил значительно упрощаются, в каждом из них остается не более трех неизвестных.