12. Особенности расчет статически неопределимых систем на смещение опор
Осадка опор сооружений может происходить из-за податливости грунта под фундаментом, при горных выработках, карстовых явлениях и т.д.
Система канонических уравнений при расчете сооружений на смещение опор записывается:
здесь KC - это перемещение по направлению XK вызванное смещением опор.
Перемещения опор определяют наблюдая за сооружением в процессе его эксплуатации, задаются маркшейдерами при шахтных подработках застраиваемых территорий и т.д.
13. Метод сил: использование симметрии рамы при выборе основной системы
основную систему необходимо выбрать симметричной, причем постараться, чтобы как можно большее число неизвестных было в виде прямо- и обратносимметричных усилий.
Прямосимметричные неизвестные создают симметричные эпюры моментов, а обратносимметричные неизвестные — кососимметричные эпюры. Результат перемножения таких эпюр:
=
0 .
Тогда в нашем случае 12 = 21 = 0 ; 13 = 31 = 0 , и система из трех уравнений с тремя неизвестными :
11Х1 + 12Х2 + 13Х3 + 1Р =0
21Х1 + 22Х2 + 23Х3 + 2Р =0
31Х1 + 32Х2 + 33Х3 + 3Р =0 ,
после подстановки коэффициентов превращается в одно независимое уравнение :
11Х1 + 1Р =0 ;
и систему из двух уравнений с двумя неизвестными :
22Х2 + 23Х3 + 2Р =0
32Х2 + 33Х3 + 3Р =0 .
14. Расчет симметричных рам методом сил: Группировка неизвестных
Часто, при расчете симметричных рам, не удается выбрать основную систему так, чтобы все неизвестные разместились на оси симметрии. Поэтому для получения симметричных и обратно симметричных эпюр приходится в качестве неизвестных применять не отдельные силы, а группы прямо- и кососимметричных сил.
У1 = Х1 + Х2
У2 = Х1 - Х2 , 12 + 21 = 0.
таким образом система уравнений:
(2)
преобразуется:
11 X1+ 1P = 0;
и
22 X2+ 2P = 0
15. Расчет симметричных рам методом сил: Преобразование нагрузки
Любую нагрузку, приложенную к симметричной раме, можно разложить на составляющие симметричного и кососимметричного вида.
q/2
q/2
Х
2
=0 X2
X1 =0 X1
P P/2 P/2
= 4
q
/2
X4
X3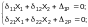 
q /2
X
3
P/2 X4 P/2 
II
С умма двух загружений I + II
дает исходное загружение
При загружении рамы симметричной нагрузкой в симметричных связях будут возникать только симметричные неизвестные усилия, а при загружении обратно симметричной нагрузкой — обратно симметричные усилия (см. рисунок).
16. Порядок расчета рам методом сил
1. Определяют степень статической неопределимости системы:
= CОП + 2Ш0 - 3D;
или
= 3K- Ш0 ;
2. Выбирают наиболее рациональную основную систему метода сил (с учетом возможных упрощений).
3. Записывают систему канонических уравнений метода сил.
4. Для основной системы строят единичные Mi и грузовую MP эпюры моментов.
5. Определяют коэффициенты системы канонических уравнений.
6. Проверяют правильность вычисления коэффициентов (универсальная, построчная и проверка грузовых коэффициентов).
7. Решают систему канонических уравнений и определяют значение неизвестных X1 ,X2 ,....,Xn . Правильность решения системы следует проверить подстановкой найденных неизвестных в систему уравнений.
8. Строят исправленные эпюры MiXi
9.
Суммируя исправленные эпюры и грузовую,
получают результирующую эпюру
10. Проверяют правильность построения эпюры MРЕЗ:
а) должно выполнятся равенство моментов в узлах;
в)
деформационная проверка (
)
= 0.
11. По эпюре MРЕЗ строят эпюру поперечных сил Q и затем по эпюре Q - эпюру продольных сил N.
12. Выполняется статическая проверка равновесия рамы в целом :
MK = 0;
x = 0;
y = 0;
в эти уравнения входит заданная нагрузка и опорные реакции, которые берут из эпюр MРЕЗ , Q, N.
13. В случае необходимости определяют перемещения указанных сечений рамы.