Добавил:

darkl0rd Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Запорожский национальный технический университет

Предмет:

Высшая математика

Файл:

Матан 1 и 2 курс-20191213T204734Z-001 / 2_5199424839454033100

.pdf

Скачиваний:

Добавлен:

13.12.2019

Размер:

497.12 Кб

Скачать

☆

1 / 81 2 3 4 5 6 7 8 > Следующая >>>

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ Запорізький національний технічний університет

МЕТОДИЧНІ ВКАЗІВКИ

для практичних занять та самостійної роботи студентів денної форми навчання

факультетів радіоприладобудівного та інформатики і обчислювальної техніки

з курсу

“ТЕОРІЯ ФУНКЦІЙ КОМПЛЕКСНОЇ ЗМІННОЇ ТА ОПЕРАЦІЙНЕ ЧИСЛЕННЯ”

2009

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

Методичні вказівки для практичних занять та самостійної роботи студентів денної форми навчання факультетів радіоприладобудівного та інформатики і обчислювальної техніки з курсу “Теорія функцій комплексної змінної та операційне числення” /Укл.: Г.А. Шишканова, Т. І. Левицька, , І. С. Пожуєва. – Запоріжжя:

ЗНТУ, 2009. – 73 с.

Укладачі:	Г.А. Шишканова, доцент, к.т.н.
	Т. І. Левицька, доцент, к.т.н.
	І. С. Пожуєва, доцент, к.т.н.

Експерт спеціальності: В.С. Кабак, доцент, к.т.н.

Рецензент: Ю. В. Мастиновський, доцент, к.т.н.

Відповідальний за випуск: Т. І. Левицька, доцент, к.т.н.

	Затверджено радою РП факультета	Затверджено на засіданні
	Затверджено радою РП факультета	кафедри прикладної математики
	ЗНТУ	ЗНТУ
	Протокол № 5 від 15.01.09	ЗНТУ
	Протокол № 5 від 15.01.09
		Протокол № 6 від 27.12.08

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

ЗМІСТ

Вступ .......................................................................................................		4
1 ТЕОРІЯ ФУНКЦІЙ КОМПЛЕКСНОЇ ЗМІННОЇ ......................		5
1.1	Комплексні числа та дії над ними ...........................................	5
1.2	Основні елементарні функції комплексної змінної ..............	10
1.3	Аналітичні функції.................................................................	13
1.4	Інтегрування функції комплексної змінної ...........................	14
1.5	Інтегральна формула Коші ....................................................	18
1.6	Ряди Тейлора та Лорана.........................................................	21
1.7	Нулі аналітичної функції .......................................................	28
1.8	Ізольовані особливі точки......................................................	29
1.9	Лишки.....................................................................................	30
2 ОПЕРАЦІЙНЕ ЧИСЛЕННЯ.......................................................		34

2.1Визначення перетворення Лапласа. Оригінал та

	зображення функції................................................................	34
2.2	Властивості перетворення Лапласа .......................................	35
2.3	Знаходження оригінала по зображенню................................	40

2.4Розв’язання задачі Коші для звичайних лінійних

		диференціальних рівнянь з постійними коефіцієнтами........	43
3	ІНДИВІДУАЛЬНІ ЗАВДАННЯ...................................................		46
	3.1	Завдання 1 ............................................................................	466
	3.2	Завдання 2 ............................................................................	466
	3.3	Завдання 3 ............................................................................	507
	3.4	Завдання 4 ..............................................................................	48
	3.5	Завдання 5 ..............................................................................	50
	3.6	Завдання 6 ............................................................................	562
	3.7	Завдання 7 ..............................................................................	53
	3.8	Завдання 8 ..............................................................................	56
	3.9	Завдання 9 ..............................................................................	57
	3.10	Завдання 10.............................................................................	58
	3.11	Завдання 11.............................................................................	63
	3.12	Завдання 12.............................................................................	67
	3.13	Завдання 13...........................................................................	688
4	ІНДИВІДУАЛЬНІ ЗАВДАННЯ...................................................		70
Література..................................................................................................			72
Додаток А.Таблиця зображень основних елементарних функцій.......			73

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

ВСТУП

Методичні вказівки складені у відповідності до програми з курсу теорії комплексної змінної та операційного числення багатоступеневої підготовки фахівців і призначені для студентів денної форми навчання та для самостійної роботи, що навчаються на факультетах радіоприладобудівному та інформатики і обчислювальної техніки.

У перших двох параграфах наведено стисло викладений теоретичний матеріал, проілюстрований багатьма прикладами, рисунками, зразками типових вправ.

Індивідуальні завдання містять 30 варіантів. Номер варіанту визначається за номером у списку журналу академічної групи.

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

1 ТЕОРІЯ ФУНКЦІЙ КОМПЛЕКСНОЇ ЗМІННОЇ

1.1 Комплексні числа та дії над ними

Комплексним числом z в алгебраїчній формі називається вираз z=х+iу, де х та у – дійсні, а i – уявна одиниця, i2 = −1. z = x − iy –

спряжене комплексне число.

x = Re z – дійсна частина комплексного числа, y = Im z –

його уявна частина.

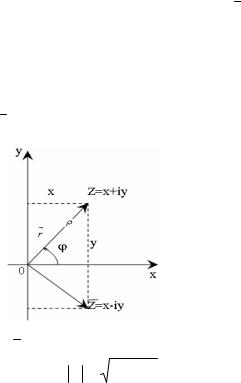
Комплексне число z=х+iу можна зобразити точкою площини хОу з координатами (х,у), також числу z можна поставити у

відповідність вектор r , який має напрямок з початку координат О в точку z (рис. 1.1).

Рисунок 1.1
Довжина вектора r має назву модуля комплексного числа:
ρ = z = x2 + y2	(1.1)

Кут ϕ , утворений з віссю Ох має назву аргумента ϕ = Argz , значення якого неоднозначне, всі його значення відрізняються на доданки, кратні 2π .

Якщо z=0, то Argz невизначено.

Головне значення аргумента позначається arg z і визначається

однозначно −π < arg z ≤ π .
ϕ = Argz = arg z + 2kπ	( k = 0;±1;± 2;....)	(1.2)

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

				ì	y
				ïarctg		,	якщо х > 0
				ïarctg	x	,	якщо х > 0
				ï	x		y
				ï						(1.3)
				ï						(1.3)
			arg z =	íπ + arctg				,	якщо х < 0, y ³ 0
			arg z =	íπ + arctg			x	,	якщо х < 0, y ³ 0
				ï			x	y
				ï				y
				ï-π + arctg					, якщо х < 0, y < 0
				ï-π + arctg				x	, якщо х < 0, y < 0
	π			î				x
arg z =	π	, якщо x=0, y>0.
	2	π
arg z = −		π	, якщо x=0, y<0.
		2

З рисунку 1.1 видно, що x = ρ cosϕ; x = ρ sin ϕ , тобто

комплексне число можна записати у так званій тригонометричній формі:

z = x + iy = ρ(cosϕ + i sin ϕ)

(1.4)

Показникова форма комплексного числа:

z = ρeiϕ

Дії над комплексними числами:

Нехай z1 = x1 + iy1 , z2 = x2 + iy2

z1 = z2 x1 = x2, y1 = y2

z1 ± z2 = (x1 ± x2 ) + i( y1 ± y2 )

z1 × z2 = (x1x2 - y1 y2 ) + i(x1y2 + x2 y1) =

= ρ ρ

(cos(ϕ + ϕ

)+ isin(ϕ +ϕ

))= ρ ρ

ei(ϕ1 +ϕ2 )

ρ1

(cos(ϕ −ϕ

))=

ρ1

)

+ isin(ϕ −ϕ

ei(ϕ1 −ϕ2 )

z2 z2

ρ2

(1.5)

(1.6)

(1.7)

(1.8)

(1.9)

Приклад 1.1

Визначити множину точок, які задовольняють наступним


умовам:	а) 1≤		z −1− i		≤ 3
умовам:	а) 1≤		z −1− i		≤ 3
	б) −	π		< arg(z −1− 2i) ≤		π
		4				6

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

Розв’язок

а) З геометричної точки зору рівняння z − z0 = r є рівнянням кола з центром в точці z0 і радіусом r .

Шукана множина точок повинна одночасно задовольняти двом умовам:

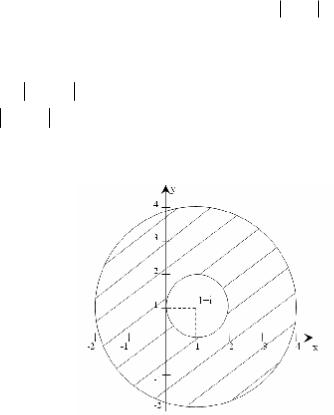
1. 1≤ z −1− i – зовнішність одиничного кола з центром в точці 1+і. 2. z −1− i ≤ 3 – внутрішність кола з радіусом 3 і центром в точці 1+і.

Тому шукана множина – це кільце, що обмежено концентричними колами радіусів 1 та 3 з центром в точці 1+і, включаючи самі кола (рис. 1.2).

Рисунок 1.2

б) комплексне число z-1-2i=z-(1+2i) зображується вектором, початок якого є точка 1+2i, а кінець – точка z.

Кут між цим вектором та віссю Ох ϕ = arg(z −1− 2i) та він змінюються у межах від − π4 до π6 .

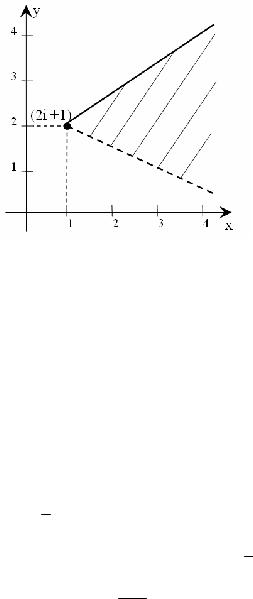
Тобто шукана множина точок – це частина площини між променями, що виходять з точки (1+2i), та які утворюють з віссю Ох

кути − π4 та π6 , включаючи верхній промінь (рис. 1.3).

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

Рисунок 1.3

Приклад 1.2

Зобразити лінію, для якої Re z2 = a2

Розв’язок

а) Знайдемо z2 : z2 = (x + iy)2 = x2 − y2 + i2xy , тоді Re z2 = x2 − y2 , тобто рівняння Re z2 = a2 можна записати так:

x2 − y2 = a2

Це, як відомо, рівнобічна гіпербола.

Для піднесення в степінь використовують формулу Муавра:

zn = ρ n (cos nϕ + i sin nϕ)

(1.10)

Приклад 1.3

Обчислити (− 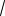3 − i)5

Розв’язок

а) Знайдемо тригонометричну форму числа (− 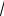3 − i). Для цього знайдемо його модуль за формулою (1.1):

ρ = 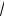3 +1 = 2

Та аргумент за формулою (1.2):

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

ϕ = arg z = -π + arctg

−1

= -π + π

= -

5π

Тоді за формулою (1.4):

- 3

5π ö

5π öö

3 - i = 2çcosç

+ i sinç-

÷÷

6 ø

øø

Використовуючи формулу (1.10), одержуємо:

25π

(- 3

- i)

= 2

çcosç-

+ i sinç

÷ =

π ö

öö

= 32çcosç

÷ + i sinç

÷÷

- i

=16 3

-16i

= 32

6 ø

øø

Корені степеня n визначаються за формулою:

ϕ + 2kπ

z = n

+ isin

= 0,1,2....n -1 (1.11)

ρçcos

÷, k

Приклад 1.4

Знайти а) 3

;

б) 3

1+ i

Розв’язок

а) Для числа 1+і

| z |=

ϕ = arg z = arctg

1+1

1+ i =

+ i sin

2çcos

Використовуючи формулу (1.11):

+ 2πk

+ i

cos

+ i sin

k = 0,1, 2

ми одержимо три різних значення кореня:

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

= 6

+ i sin

(k = 0)

2çcos

÷,

12 ø

z2 = 6

9π

+ isin

9π ö

(k =1)

2çcos

÷,

12 ø

= 6

17π

+ isin

17π

(k = 2)

2çcos

÷,

12 ø

б) для числа z=1:

ρ =1; ϕ = 0 , за формулою (1.11):

3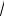1 = cos 2π3k + i sin 2π3k , z1 = cos0 + i sin 0 =1,

z2 = cos 23π + i sin 23π = - z3 = cos 43π + i sin 43π = -

		k = 0,1, 2
(k = 0)
1				i,
	+		3		(k =1)
2		2

1
	-		3	і,	(k = 2)
2		2

1.2 Основні елементарні функції комплексної змінної

Показникова функція					ez обчислюється за допомогою
формули Ейлера:					= ex(cos y + isin y)
		ez = ex+iy
Тригонометричні функції sinz i cosz можна обчислити за
формулами
sin z =	eiz − e−iz			,	cos z =	eiz + e−iz

		2i			2
Функції tgz i ctgz визначаються рівностями
tg z =		sin z	,		ctg z =		cos z
							sin z
		cos z

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

1 / 81 2 3 4 5 6 7 8 > Следующая >>>

Соседние файлы в папке Матан 1 и 2 курс-20191213T204734Z-001

#
13.12.2019497.12 Кб312_5199424839454033100.pdf
#
13.12.2019422.2 Кб29ty_metodychka_a5_2nd_ed.pdf