2.2.3 Транспортна задача

Розглядається m пунктів виробництва та n пунктів споживання деякої однорідної продукції. Відомі обсяги виробництва продукції у кожному i-му пункті – та потреби кожного j-го пункту споживання – . Також задана матриця розмірністю , елементи якої є вартостями транспортування одиниці продукції з i-го пункту виробництва до j-го пункту споживання. Необхідно визначити оптимальні обсяги перевезень продукції з урахуванням наявності продукції у виробників та забезпечення вимог споживачів.

Критерій оптимальності: мінімальна сумарна вартість перевезень.

Позначимо через х_ij обсяг продукції, що перевозиться від i-го виробника до j-го споживача.

Можна вивезти від кожного виробника продукцію, що є в наявності. Тому для кожного і має виконуватись умова: . Забезпечення кожного споживача потрібною кількістю продукції дає умова: для кожного . Загальна вартість перевезень є сумою добутків . Необхідно, щоб виконувалась умова . Отже, економіко-математична модель транспортної задачі має такий вигляд:

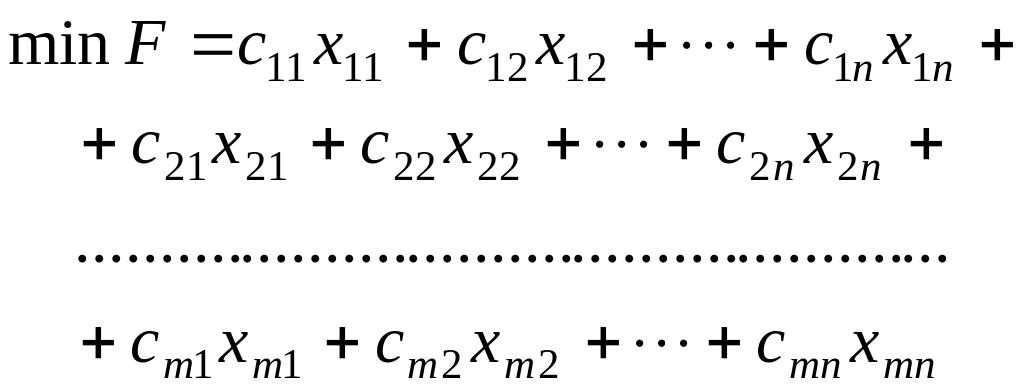
за умов:

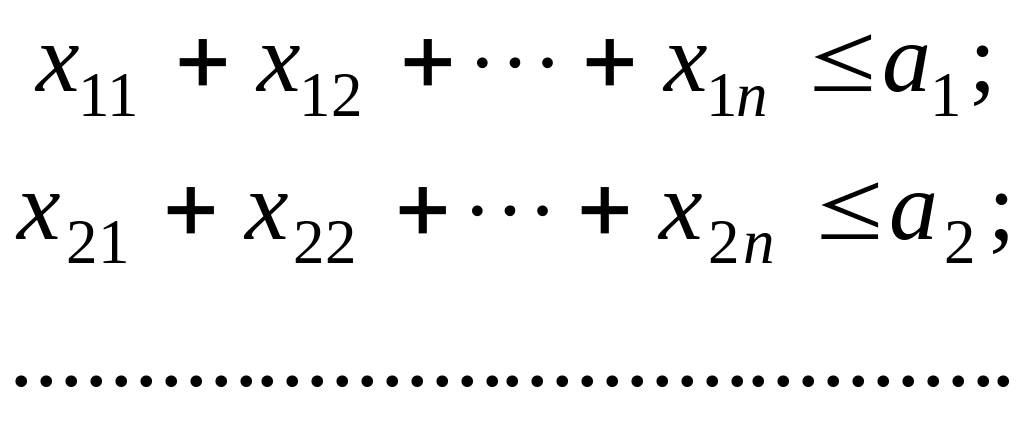
Як і в двох попередніх задачах математична модель транспорт­ної задачі може використовуватись і тоді, коли в постановці задачі немає навіть згадки про перевезення продукції тощо.

Приклад 2.6. Фермерське господарство спеціалізується на вирощуванні озимої пшениці і має три ділянки землі площею S₁ = 40 га, S₂ = 90 га, S₃ = 55 га. Враховуючи наявну кількість посівного матеріалу, є можливість засіяти всю площу озимою пшеницею трьох сортів. Кількість пшениці сорту «Миронівська-808» забезпечить посів на 80 га, «Безоста-1» – 60 га та «Одеська-51» – 45 га. Урожайність сорту «Миронівська-808» на даних ділянках становить відповідно 41 ц/га, 40 ц/га, 46 ц/га. Аналогічно для сорту «Безоста-1» маємо: 38 ц/га, 41 ц/га, 45 ц/га, а для «Одеської-51» — 30 ц/га, 28 ц/га, 40 ц/га.

Необхідно розподілити посівний матеріал за земельними ділянками так, щоб отримати максимальний урожай (валовий збір) озимої пшениці.

Побудова економіко-математичної моделі.

Позначимо через х_ij площу (га) і-ої земельної ділянки, що буде засіяна j-м сортом озимої пшениці (домовимося, що сорти «Миронівська-808», «Безоста-1», «Одеська-51» відповідатимуть номерам 1, 2, 3), (і = 1, 2, 3), (j = 1, 2, 3).

Тоді використання земельних угідь описуватиме така система обмежень:

;

;

.

Використання посівного матеріалу формально можна описати так:

;

;

.

Валовий збір зерна розраховується як сума добутків урожайностей відповідних сортів пшениці на їх посівні площі, тобто:

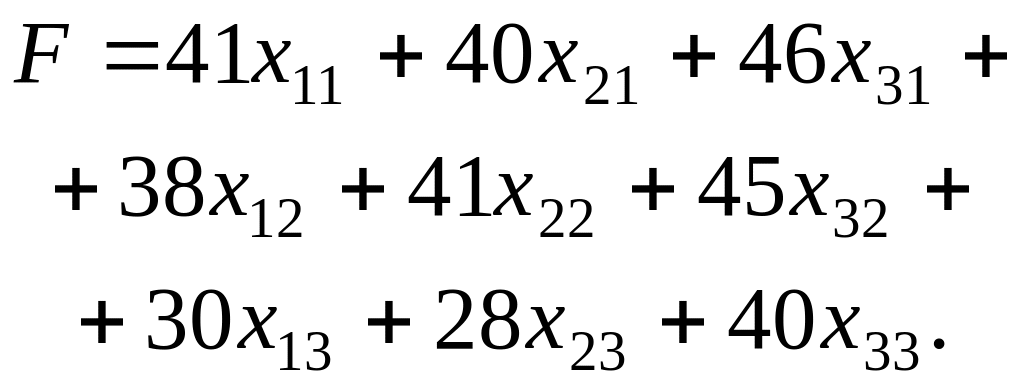
Отже, економіко-математична модель задачі загалом буде мати вигляд:

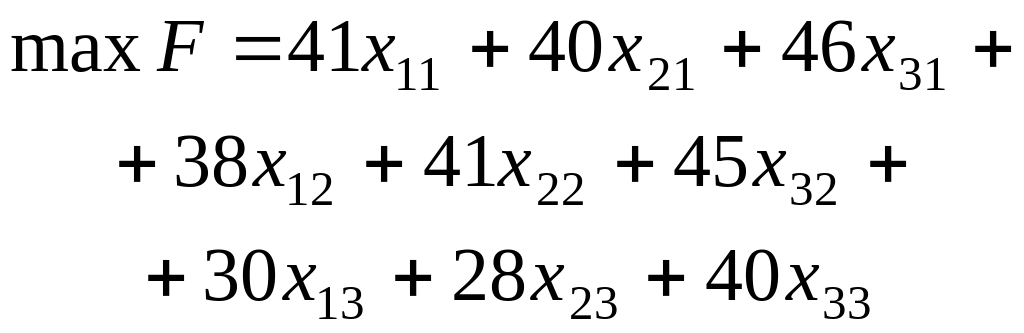
за умов:

.

Самостійна робота №2 – Економіко-математичні моделі задач лінійного програмування

Економіко-математична модель задачі визначення оптимального плану виробництва. Економіко-математична модель задачі оптимального розподілу виробничих потужностей. Економіко-математична модель задачі оптимального розподілу капіталовкладень. Економіко-математична модель задачі про «дієту». Економіко-математична модель транспортної задачі. Економіко-математична модель задачі про призначення. Економіко-математична модель задачі комівояжера [3, с.23-36].

3. Наконечний С. І., Савіна С. С. Математичне програмування: Навч. посіб. – К.: КНЕУ, 2003. – 452 с.