14.Найпростіші властивості числових рядів

Запишемо ( без доведення ) декілька властивостей числових рядів.

1. Відкидання скінченної кількості перших членів ряду не впливає на його збіжність; якщо вихідний ряд збіжний, то сума отриманого ряду буде менша суми початкового ряду  на суму відкинутих членів.

2. Збіжні ряди можна почленно додавати і віднімати. Ця властивість означає, що із збіжності двох рядів   випливає збіжність ряду

Крім того, якщо суми цих рядів позначити через А,В,С відповідно, то має місце рівність С=А±В.

Слід відмітити, що із збіжності ряду     

 збіжність рядів   не випливає.

Наприклад, збіжний ряд 0+0+0+… отриманий в результаті почленного додавання розбіжних рядів 1+1+1+… і -1-1-1…     .

3. Якщо члени збіжного ряду, не змінюючи їх порядку, об'єднати в групи, то отриманий при цьому ряд також збігається  і сума його співпадає із сумою вихідного ряду.

Зокрема, в прикладі 2 ми показали, що ряд

   збігається .

За даною властивістю буде збігатись і ряд

Ця властивість необоротна: розкриття дужок в збіжному ряді може привести до розбіжного ряду. Це видно на прикладі ряду(1-1)+(1-1)+ який збігається, оскільки кожний його член рівний нулю. В той же час, розкривши дужки, ми отримаємо розбіжний ряд 1-1+1-1+… 

4. Нехай   - деякий збіжний числовий ряд,   - сума цього ряду. Тоді ряд   (С – довільне число, відмінне від нуля) також збіжний і його сума рівна  .

5. Нехай ряд   з невід‘ємними членами, а ряд   отримується із даного ряду довільною перестановкою його членів. Тоді дані ряди збігаються одночасно і мають одну і ту ж суму.

15Знакододатні ряди. Достатні ознаки збіжності.

Якщо 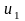, ,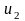... ,...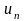— нескінченна числова послідовність, то вираз

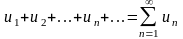
називається числовим рядом, а величини , ,...— членами цього ряду.

Побудуємо допоміжну послідовність частинних сум ряду 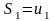, ,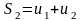... ,...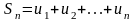 . Якщо ця послідовність має скінчену границю 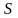, то ряд називається збіжним, а число — сумою ряду. У випадку, коли границя не існує або є нескінченною, ряд називається розбіжним.

Якщо всі члени ряду є додатними, то ряд називається знакододатним.

Необхідна умова збіжності числового ряду

Якщо ряд 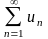є збіжним, то послідовність його членів прямує до нуля, тобто .

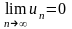Наслідок. Якщо 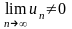, то ряд є розбіжним.

Достатні умови збіжності знакододатних рядів

Ознака порівняння.

Якщо для членів знакододатних рядів справджується нерівність 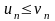, та ряд 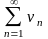є збіжним, то ряд також збігається.

Якщо для членів знакододатних рядів справджується нерівність 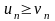, та ряд є розбіжним, то ряд також розбігається.

Якщо для членів знакододатних рядів має місце умова 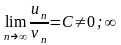, то ряди та збігаються або розбігаються одночасно.

Найчастіше для порівняння використовується узагальнений гармонічний

ряд (або ряд Діріхле) 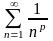. Цей ряд збігається, якщо 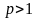, та розбігається у

випадку .

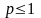Ознака Даламбера.

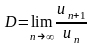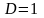Ряд збігається, якщо параметр менший за 1, та розбігається, якщо це число більше за 1. У випадку поведінку ряду за допомогою ознаки Даламбера визначити неможливо.

Радикальна ознака Коші

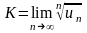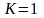Ряд збігається, якщо параметр менший за 1, та розбігається, якщо це число більше за 1. У випадку поведінку ряду за допомогою радикальної ознаки Коші визначити неможливо.

Інтегральна ознака Коші

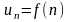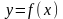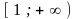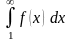Нехай загальний член ряду задано рівністю , та функція є додатною та спадною на проміжку . Тоді невласний інтеграл та ряд збігаються або розбігаються одночасно.

При розв’язуванні задач доцільно обирати ознаку для дослідження, користуючись порадами, які наведені у вигляді таблиці.