2. Матрица линейного оператора, нахождение координат образа вектора

Пусть A:V W- линейное отображениеn-мерного пространстваV вm-мерное пространствоW. Зафиксируем в пространствеV произвольный базисe1…n, а в пространствеW базисf1…n. Линейное отображение одозначно задается образами базисных векторов. Разложим образы A(ei) базис векторовe по базисf: Из координатных столбцов веткоров A(e1),…,A(en) относительно базиса(f) составим матрицу размеромm*n A= - она называетсяматрицей линейного отображения А в базисах(e) и(f). Обозначают

Нахождение координат образа вектора: еслив базисе(имеет координатный столбецX=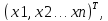f – линейный оператора с матрицей А в данном базисе,Y=- координаты столбец вектора, тоY=AX (

3. Действия с линейными операторами. Линейное пространство ло

Действия:

1. Линейный оператор А: X->Y, нулевой элмент Ox пространства X переводит в нулевой элементOy, пространства Y. AOx=Oy

2. Два линейных оператора А и В: X->Y называются равными, если для любого x из X справедливоAx=Bx

3. Суммой двух линейных операторов А и В: X->Y называется операторA+B, такой, что для любого х из Х справедливо(A+b)x=Ax+Bx

4. Произведением линейного оператора A на числоλ, называется операторλA, такой, что для любогоx из Х:(λA)x=λ(Ax)

Свойства: еслиA, B, а Аеи Be – соответственно их матрицы в базисе {e}, то: λ(AB)=(λA)B; (A+B)C=AC+BC; A(B+C)=AB+AC; (AB)C=A(BC)

Линейное пространство: ОбозначимL(L,L’) множество всех линейных операторов, действующих изL -> L’. В этом множестве введем операции сложения, умножения линейных операторов и умножения на действительное число. Таким образом, относительно введеных нами действий множество L(L,L’) замкнуто. И по аксиомам линейного пространство, относительно этих действий множество является линейным пространством.

4. Теорема об изоморфности множества линейных преобразований множеству квадратных матриц

Из утверждения о том, что любому оператору Aможно поставить в соотвествие матрицуАе в базисе [e], причем она будет определена единственным образом, а также из свойств действий с этими матрицами следует, что пространствоL(Vn) изоморфнопространству квадратных матриц порядкаn, размерность которого равнаn^2. dimL(Vn)=n^2

5. Матрица произведения линейных преобразований. Примеры нахождение матриц операторов.

Пусть произведением линейных преобразований иявляется преобразование, определяемое равенством () = (а), то есть получающееся в результате последовательного применения преобразованийи.

Тогда Матрица произведения линейных преобразованийв любом базисе равна произведению матриц этих преобразований в том же базисе:

=> е(jy) = (АВ)е

Примеры: 1) Пусть А – оператор поворота плоскости на уголf, а вектора e1 e2 – ОНБ на плоскости. Очеивдно, что Ae1=cosfe1+sinfe2, Ae2=-sinfe1+cosfe2. Следовательно,

2) Пусть Mn – пространство многочленов степени. Рассмотрим в нем оператор дифференцирования А:. Выберем в пространствеMn базисe1=1, e2=t, e3=t^2… en=t^n-1. ТогдаAe1=0, Ae2=1=e, Ae3=2t=e2e2…. Aen=(n-1)t^n-2=(n-1)en-1. Следовательно матрица оператора А в этом базисе имеет вид:

6. Определение и свойства обратного оператора, его матрица.

Если для оператора Aсуществует, чтоAB=BA=1, то B называетсяобратнымпо отношению кA,а оператор А называется обратимым. Обозначается

Свойства: если для оператора Асуществует обратный, то:

1. L(X), т.е. - тоже линейный.

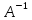2. определен однозначно.

Матрица обратного оператора в любом базисе е есть обратная матрица к матрице Ае