11. Неоднородные слау. Теорема о структуре решения неоднородной слау. Алгоритм решения неоднородной слау.

СЛАУ называется неоднородной, если все правые части уравнений, входящих в нее, не равны нулю одновременно.

Теорема о решении неоднородной СЛАУ – Общее решение неоднородной совместной системыAx=b есть сумма какого-нибудь частного решения системы и общего решения однородной системы x(OH)=x(ЧН) +x(ОО)

Доказательство: Пусть х – произвольное решение неоднородное системыAx=b, a х(ЧН) - ее частное решение. Тогда А(x-x(ЧН))=Ax-Ах(ЧН)=b-b=0 => х-х(ЧН) – есть решение однородной системы, т.е.x=x(ЧН)+х(ОО) чтд.

1. Определение линейного (векторного) пространства. Примеры лп.

Линейное пространство – непустое множествоV элементов произвольной природы, если для эти элементов определены операции сложения и умножения на вещественные (комплексные) числа и обладающие для любых x, y, z из множестваV и любых чиселλ, u свойствами:

Cуществует нулевой элемент, такой что x+0=x

Для любого элемента x из множества V существует противоположный элемент x', такой что х+x’=0

Для любого x множества V 1*x=x

Пример: Обозначим{o}— множество, содержащее один нулевой вектор, с операциями o+o=o иλo=o. Для указанных операций cвойства выполняются. Следовательно, множество  является линейным пространством над любым числовым полем. Это линейное пространство называется нулевым.

2. Линейно зависимые и линейно независимые системы векторов. Критерий линейной зависимости.

Элементы x1,x2,x3….xn линейного пространства V называются линейно независимыми, если из равенства λ1x1+λ2x2+…λkxk=0, cледует, что λ1=λ2=…=λk=0, гдеλ – любые числа.

Если λ1x1+λ2x2+…λkxk=0 справедливо, однако не все λ равны 0, то элементы из линейного пространстваV –линейно зависимы.

Критерий линейной зависимости– Элементы x линейного пространства линейно зависимы тогда и только тогда, когда один из элементов является линейной комбинацией остальных.

Пусть один из элементов – линейная комбинация остальных, т.е. имеет место равенство x1=b2x2+b3x3…+bkxk

Так как среди чисел b по крайней мере одно отлично от нуля, то согласно определению элементы x1, x2… xk – линейно зависимы.

3. Достаточные условия линейной зависимости и линейной независимости систем векторов лп. Примеры линейно независимых систем в пространствах строк, многочленов, матриц.

1. Если среди элементов x1,x2,…xk имеется нулевой, то элементы x1, x2,…xk линейно зависимы. Без ограничения общности можно считать, чтоx1=0. Тогда λ1x1+λ2x2+…λkxk=0 справедливо приλ1=1, λ2…λk=0

2. Если в системе элементов x некоторая подсистема элементов линейно зависима, то и вся система x линейно зависима. Пусть для определенности элементы х линейно зависимы, т.е. справедливы равенстваλ1x1+λ2x2+…λkxk=0 при λ не равном 0. Тогда с теми же числами λ1,λ2,…λλ иλλ+λ1 = … λk=0.

3. Если вся система элементов линейно независима, то и любоая подсистема элементов линейно независима. Предполагая линейную зависимость подсистемы элементов, согласно предыдущему свойству получаем, что и вся система элементов линейно зависима, что противоречит условию.

Примеры:

1. В пространстве A элементы e1…k – cтрочки единичной матрицы 4х4 линейно независимы. Действительно, линейная комбинация элементовe1..k с числамиλ1…k представляет собой элементλ1e1+λ2e2+…λkek=(λ1,λ2,…λk), который является нулевым только при условии λ1=λ2=…=λk=0. А это значит линейную независимость элементов e1…k

2. В пространстве Pn(t) многочленов степени, не превышающей натурального числа n, элементы1,t,t^2,…t^n линейно независимы. Действительно, то, что линейная комбинация этих элементов с коэффициентами λ0,λ1,λ2…λn равна нулевому элементу, означает что многочлен λ0+λ1t+λ2t^2+…λnt^n тождественно равен 0. Для любогоk=1…n, дифференцируя последнее равенство по tk раз и подставляяt=0, получимk!λk=0. Это и и означает что1, t, t^2, … t^n линейно независимы.

3. В пространстве Mmn всех матриц порядка m*n матрицы Еij, (E0 матрица, у которой элемент, состоящий на пересеченииi-ой строки и j-ого столбца равен 1, а все остальные элементы равны 0) линейно независимы. Действительно, линейная комбинация элементовE0 с числамиλij представляет собой матрицу элементов λ, которая является нулевой только при условииλij=0, гдеi=1…m; j=1…n;

4. Базис и размерность ЛП. Свойство базисных элементов, координаты суммы двух векторов и произведение вектора на число. Теорема о связи базиса и размерности ЛП. Примеры базисов в ЛП строк, многочленов, матриц.

Размерность пространства-dimV=n количество линейно независимых элементов в линейном пространстве, таких что, любые n+1 элементы линейно зависимы.

Базис пространства– упорядоченная совокупность элементов линейного пространства, если она линейно независимая и для любого элемента данного пространства найдутся числа, такие, что справедливо равенство:. Такое представление называется разложением элемента по базису, а числакомпонентами (координатами) элемента в данном базисе.

Для любого элемента линейного пространства координаты в данном базисе определяются единственным способом.

Док-во: Допустим, что в пространстведля элемента существует два разложения по базису. Вычитывая из первого второе, получаем(Так как e1,e2,…en линейно независимы, то из последнего равенство следуетчтд

Теорема … - Пусть в конечномерном пространстве задан некоторый базис. Тогда при сложении любых элементов пространства, координаты их (относительного этого базиса) складываются: при умножении любого элемента из пространства на числоλ все координаты умножаются на λ.

Док-во : Утверждение теоремы следует из аксиом линейного пространства и определения базиса.

Теорема о связи базиса и размерность –

А) Если V – конечномерное простраснтво размерности n, то всякие n линейно независмых элементов пространства образуют базис этого пространства.

Б) Если в линейном пространстве имеется базис, состоящий из n элементов, то размерность пространства равна n.

Док-во:

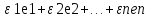А) Пусть e1…n – произвольная линейно независимая система элементов пространства. Если х – произвольный элемент пространства, то согласно определению размерности элементы e1…n, x линейно зависимы, т.е. существуют числа λ1…n не все равные нулю, такие, что λ1e1+λ2e2+…λnen=0. Из теоремы выше следует, чтоλn+1и следовательно, x=, где. Так как х – произвольный элемент пространства, то последнее равенство доказывает первую часть теоремы.

Б) пусть e1…n – базис пространства. Для завершения доказательства теоремы достаточно показать, что любые n+1 элементы x1…n+1 линейного пространства линейно зависимы. Разложим каждый элемент из системы х по базисуe. Рассматривая матрицу A координат вектораx в базисе е очевидно, чтоrangAn. Следовательно по теореме о базисном миноре строки данной матрицы линейно зависимы, т.е. существуют такие числа λ , что, где a –координаты вектора х в базисе e. Умножая каждоеxi из первомого разложения на λi, i=1…n+1 и суммируя по i получаем

Учитывая равенство что , получае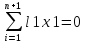м, причем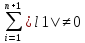

Следовательно x1…n – kинейно зависимы. Чтд

Примеры: В пространстве A^n элементы е1…n являющиеся строками единичной матрицы линейно независимы. Кроме того, для любого х=(Следовательно, элементы e1…n являются базисом пространстваA^n по определению.

В пространстве Pn(t) –многочленов степени, не превышающей натурального числа n элементыe1=1, e2=t, en+1=t^n линейно независимы. Кроме того, для любого многочлена Pn(t)=a1e1+a2e2+…anen+1. Следоватльно, многочлены e1=1, e2=t, en+1=t^n образуеют в пространстве Pn(t) базис иdimPn(t)=n+1

В пространстве Mmn всех матриц порядкаm*n матрицыEij образуют базис, так как они линейно независимы и для любой матрицыA=[aij] имеет место разложение. Следовательно dimMmn=mn