9. Подпространство решений однородной слау, его размерность и базис. Выражение общего решения однородной слау через фср.

Множество решенийсистемы линейных однородных уравнений с n переменными есть линейное подпространство арифметического пространства Аn .

Размерностьпространства решений системы линейных однородных уравнений равна n – r, где n – число неизвестных, r – ранг матрицы системы

Базиспространства решений системы линейных однородных уравнений называется её фундаментальной системой решений.

Если а – частное решение линейной неоднородной системы уравнений и а1, а2, …, аn–r – фундаментальная система решенийсоответствующей однородной системы уравнений, то общее решение данной неоднородной системы имеет вид

d = а + С1а1 + С2а2 + … + Сn–r аn–r , где С1, С2, … , Сn–r – любые элементы поля Р.

(Иными словами, общее решение системы линейных неоднородных уравнений равно сумме частного решения этой системы и общего решения соответствующей однородной системы.)

10. Матрица перехода от одного базиса лп к другому и ее свойства. Преобразование координат вектора при переходе к другому базису.

Пусть в линейном пространстве заданы два базиса:e = (e₁, e₂, …, e_n)(назовём его старым базисом) и= (e₁', e₂', …, e_n')(назовём его новым базисом).

Разложим векторы базиса e^' по базисуe:

Матрицу Т=называютматрицей переходаот базисаeк базису. Равенства в матричном виде удобно записывать так:=е·Т.

Свойства: , Матрица перехода невырожденная(квадратная, определитель не 0).

Преобразование координат: Пусть в линейном пространствезаданы базисы e=(e1,e2,…,en) и=(e1',e2', …,en') с матрицей перехода Т от базиса е к базису e', т.е. верно=еТ (2). Вектор а имеет в базисах е икоординаты[a]e=, [a]e’=,

a=e*[a]e=(e1,e2,…en)иa=e’[a]e’=(e1’,e2’,….en’).

Тогда с одной стороны, а=е*[a]e, а с другой стороны а= e’[a]e’=(еТ)[a]e’

Из этих равенств получаем: а=e[a]e=е(Т[a]e'). Отсюда в силу единственности разложения вектора по базису е вытекает равенство [a]e = Т[a]e' (3), или

=Т (4). Соотношения (3) и (4) называют формулами преобразования координат при изменении базиса линейного пространства.

1. Определение и примеры линейных операторов, линейные отображения и линейные преобразования

Пусть X иY – линейные пространства. Оператором А, действующим изX вY, называется правило (закон), ставящее каждому элементуxединственный элементy. Результат применения оператораA к элементу х обозначается символомy=A(x). Элементx называется прообразом элементаy=A(x)

Оператор А, действующий из X вY, называется линейным, если для любых элементов x1 и х2 пространства Х и любых комплексных (вещественных) чиселa1 иa2 выполняется соотношение:

Примеры:

- В пространстве V свободных векторов оператор А зададим равенством:, для любого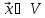, где– фиксированный вектор пространстваV. Линейность этого оператора следует из свойств векторного произведения.

- В пространстве Mn многочленов степениоператор А зададим равенством:для любогоP(t)Mn. Линейность этого оператора (оператора дифференцирования) следует из линейности операции дифференцирования.

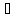Пусть V иW – два линейных пространства, тогдаотображением A:V W называетсялинейным, еслидля любых x, yV иa,b

Линейное преобразование А пространства V, есть закон, по которому каждому вектору x из A соответствует вектор x' из того же пространства. Вектор x' называется образом вектора x и обозначается A(x) , а вектор x называется прообразом вектора x' .