6. Система линейных алгебраических уравнений, основные свойства слау, однородность и неоднородность, совместность и несовместность, определенность слау, матричная форма записи слау и ее решения

Система линейных алгебраических уравнений –называется система уравнений вида:, гдеa – коэффициенты, b – свободные члены иx – неизвестные. Упорядоченый набор - называется решением системы, если при подстановке в уравнения, все уравнения превращаются в тождество. СЛАУ называетсясовместной, если она имет хотя бы одно решение. В противном случае система называется несовместной.

СЛАУ называется определенной, если она совместа и имеет единственное решение. В противном случае система называетсянеопределенной.

СЛАУ называется однородной, если все правые части уравнений, входящих в нее, равны нулю одновременно.

Слау можно записать в матричному виде: A*X=B, где матрица А – матрица системы, составленная из коэффициентов при неизвестных, Х – вектор-столбец неизвестных и В – вектор-столбец свободных коэффициентов.

7. Квадратные системы, метод Крамера

СЛАУ называется квадратной,если количество уравнений равно количеству неизвестных.

Метод Крамера - Если определитель матрицы системы не равен нулю, то он имеет единственное решение и это решение находится по формуле:, где- определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов:

8. Элементарные преобразования слау. Метод Гаусса исследования слау.

Элементарные преобразования:

1. Прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на одно и то же число, не равное нулю.

2. Перестановка уравнений местами.

3. Удаление из системы уравнений, являющихся тождествами для всех х.

Метод Гаусса:

1. Составить расширенную матрицу системы (A|b)

2. Используя элементарные преобразования привести к ступенчатому виду

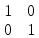
3. Выяснить совместность систем (rgA=rg(A|b)

4. Упрощение матрицы

5. Записываем матрицу как СЛАУ

6. Выражаем базисные переменные через выбранные свободные. Они являются ответом

9. Критерий совместности слау, теорема Кронекера-Капелли, геометрическая интерпретация на примере 2-х уравнений с 2-мя неизвестными.

Теорема Кронекера-Капелли:СЛАУсовместна тогда и только тогда, когдаранг матрицысистемы равен рангу расширенной матрицы.

Доказательство: Пусть система совместна. Тогда существует такие неизвестные, что b=x1a1+…xnan.Следовательно, столбецb является линейной комбинацией столбцовa1…an матрицыA. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинаций других строк (столбцов) следует, чтоrangA=rang(A|b)

10. Однородные слау. Свойство решений, фср, теорема об общем решении однородной системы. Критерий существования нетривиального решения.

СЛАУ называется однородной, если все правые части уравнений, входящих в нее, равны нулю одновременно.

Однородная система всегда совместна: у нее всегда существует решение x=0, называемое тривиальным. Решение x–нетривиальное.

Свойства:

1. Если х1 и х2 – два произвольных решения однородной системы, то для любых чисел L и U их линейная комбинацияLx1+Ux2 также является решением системы.

2. Если однородная система имеет хотя бы одно нетривиальное решение, то она имеет их бесконечно много.

3. Если rangA=n(n – количество переменных) то однородная система имеет только тривиальное решение, если же rangA=r<n, то общее решение имеет вид ,где С – произвольные числа.

Фундаментальная система решений (ФСР) – Набор линейно независимых решений однородной СЛАУКоличество элементов вФCР=n-rangА

Критерий существования нетривиального решения – СЛАУ имеет нетривиальное решение, если rangA < количества переменных.