Сортировка пузырьком
Сортировка пузырьком(англ. bubble sort) — простой алгоритм сортировки. Для понимания и реализации этот алгоритм — простейший, но эффективен он лишь для небольших массивов. Сложность алгоритма: O(n2).
Алгоритм
Алгоритм состоит в повторяющихся проходах по сортируемому массиву. За каждый проход элементы последовательно сравниваются попарно и, если порядок в паре неверный, выполняется обмен элементов. Проходы по массиву повторяются до тех пор, пока на очередном проходе не окажется, что обмены больше не нужны, что означает — массив отсортирован. При проходе алгоритма, элемент, стоящий не на своём месте, «всплывает» до нужной позиции как пузырёк в воде, отсюда и название алгоритма.
for i := n - 1 downto 1 do
for j := 1 to i do
if a[j] > a[j+1] then
begin
t := a[j];
a[j] := a[j+1];
a[j+1] := t;
end;
Сортировка простыми вставками
Сортировка вставками (англ. insertion sort) — простой алгоритм сортировки. Хотя этот метод сортировки намного менее эффективен, чем более сложные алгоритмы (такие как быстрая сортировка), у него есть ряд преимуществ:
прост в реализации
эффективен на небольших наборах данных
эффективен на наборах данных, которые уже частично отсортированы
это устойчивый алгоритм сортировки (не меняет порядок элементов, которые уже отсортированы)
может сортировать список по мере его получения
На каждом шаге алгоритма, мы выбираем один из элементов входных данных и вставляем его на нужную позицию в уже отсортированном списке, до тех пор пока набор входных данных не будет исчерпан. Выбор очередного элемента, выбираемого из исходного массива — произволен, может использоваться практически любой алгоритм выбора.
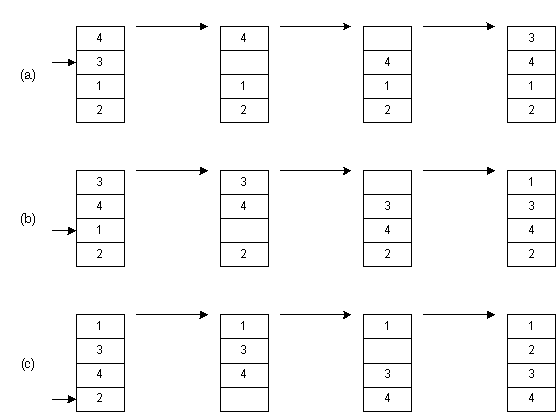
На рис (a) мы вынимаем элемент 3. Затем элементы, расположенные выше, сдвигаем вниз - до тех пор, пока не найдем место, куда нужно вставить 3. Это процесс продолжается на рис(b) для числа 1. Наконец, на рис (c) мы завершаем сортировку, поместив 2 на нужное место.
For i:=2 to Сount do
Begin
Tmp:=Arr[i];
j:=i-1;
While (Arr[j]>Tmp) and (j>0) do
Begin
Arr[j+1]:=Arr[j];
j:=j-1;
End;
Arr[j+1]:=Tmp;
End;
Сортировка Шелла (Ох и презабавная вещь).
Вариант описания №1 (длинный)
Сортировка Шелла является довольно интересной модификацией алгоритма сортировки простыми вставками.
Рассмотрим следующий алгоритм сортировки массива a[0].. a[15].
1. Вначале сортируем простыми вставками каждые 8 групп из 2-х элементов (a[0], a[8[), (a[1], a[9]), ... , (a[7], a[15]).
2. Потом сортируем каждую из четырех групп по 4 элемента (a[0], a[4], a[8], a[12]), ..., (a[3], a[7], a[11], a[15]).
В нулевой группе будут элементы 4, 12, 13, 18, в первой - 3, 5, 8, 9 и т.п.
3. Далее сортируем 2 группы по 8 элементов, начиная с (a[0], a[2], a[4], a[6], a[8], a[10], a[12], a[14]).
4. В конце сортируем вставками все 16 элементов.
Очевидно, лишь последняя сортировка необходима, чтобы расположить все элементы по своим местам. Так зачем нужны остальные ?
Hа самом деле они продвигают элементы максимально близко к соответствующим позициям, так что в последней стадии число перемещений будет весьма невелико. Последовательность и так почти отсортирована. Ускорение подтверждено многочисленными исследованиями и на практике оказывается довольно существенным.
Единственной характеристикой сортировки Шелла является приращение - расстояние между сортируемыми элементами, в зависимости от прохода. В конце приращение всегда равно единице - метод завершается обычной сортировкой вставками, но именно последовательность приращений определяет рост эффективности.
Вариант описания №2 (короткий)
Шаг 1. Упорядочиваемое множество разбивается на несколько непересекающихся подмножеств по следующему правилу:
берутся элементы неупорядоченного множества, расположенные на одинаковом расстоянии (дистанции) друг от друга. Полученные множества сортируются методом простых вставок, что позволяет уменьшить общую неупорядоченность множества.
Шаг 2. Алгоритм завершает работу, когда дистанция равна 1, иначе уменьшается дистанция между элементами и повторяется шаг 1.
Примечание:
Выбор последовательности дистанций между элементами в сортировке методом Шелла является отдельной проблемой, которая подробно рассматривается Д.Кнутом в монографии “Искусство программирования для ЭВМ. Т.3: Сортировка и поиск”.
Пример:
const N=10; {Количество элементов массива}
var a: array[1..N] of integer; {массив}
p: boolean; {флаг наличия перестановки}
l,d,i,j: integer; {служебные переменные}
...........
d:=N div 2; {Расстояние между обрабатываемыми элементами массива,
на каждом этапе алгоритма уменьшается в 2 раза вплоть до 0,
когда происходит останов алгоритма}
while d>0 do
begin
for j:=1 to N-d do {Перебор всех пар элементов массива,
расстояние между которыми равно d}
begin
l:=j {запоминаем индекс текущего элемента}
repeat
p:=false; {пока элементы не переставлялись}
if a[l]<a[l+d] then begin {если порядок нарушен, то}
c:=a[l];a[l]:=a[l+d];a[l+d]:=c; {меняем местами элементы массива}
l:=l-d; {перейдём к той паре, в которую
входит меньший из переставленных элементов}
p:=true; {запомним, что была перестановка}
end;
until (l<=1) and p; {продолжаем, пока идут перестановки и
не произошёл выход за пределы массива}
end;
d:=d div 2; {Уменьшим расстояние между сравниваемыми элементами
в 2 раза}
end;