Глава 2 екстремальні задачі на графах

2.1 Основні поняття

Графом називається сукупність двох множин U (точок) та V (ліній), між елементами яких визначено відношення інцидентності, причому кожний елемент інцидентний точно двом елементам . Елементи множини U називають вершинами графа G, елементи множини V – його ребрами. Ребро називають інцидентним вершині, якщо воно заходить у вершину або виходить з неї.

В деяких задачах інцидентні ребру вершини нерівноправні: вони розглядаються в певному порядку. Тоді кожному ребру можна приписати напрям від однієї з інцидентних вершин до іншої. Ребра, які мають напрям, називають дугами. Граф, що складається з неорієнтованих ребер, називається неорієнтованим. Граф, що складається з орієнтованих ребер (дуг), називається орієнтованим.

Послідовність вершин і ребер, де кожне ребро з’єднує дві суміжні вершини, називається маршрутом у графі. Маршрут починається з вершини і закінчується у вершині. Якщо початок і кінець маршрута співпадають, то маршрут називається циклічним.

Маршрут, усі ребра якого різні, називається ланцюгом.

Якщо початкова і кінцева вершини ланцюга співпадають, то це цикл.

Ланцюг простий, якщо всі його вершини різні (не повторюються).

Цикл простий, якщо співпадають лише початкова і кінцева вершини.

Шлях – це маршрут в орієнтованому графі, по якому потрібно рухатись, погоджуючись з покажчиком напряму. Шлях, у якому початкова і кінцева вершини співпадають, називається контуром.

Граф називається зв’язним, якщо для будь-яких вершин існує ланцюг, що їх з’єднує.

Зв’язний граф називається ейлеровим, якщо існує цикл, що проходить через кожне його ребро.

Граф називається гамільтоновим, якщо існує цикл, що проходить тільки один раз через кожну вершину графа.

2.2 Способи задання графа

Зображення графів на площині у вигляді множини точок і множини ребер (дуг) – найбільш прийнятний і наочний спосіб, але його не можна використати тоді, коли для розв’язання тієї чи іншої задачі, пов’язаної з графами, необхідне застосування комп’ютера.

Існують різні способи задання графа:

1. за допомогою матриці суміжності вершин;

2. за допомогою матриці суміжності ребер (дуг) графа;

3. за допомогою матриці інцидентності.

1 Матриця суміжності вершин

Нехай у графі число вершин дорівнює n. Матриця суміжності вершин орієнтованого графа R=(r_ij) має розмір ,

де

Якщо граф неорієнтований, вершини з’єднуються ребрами і матриця R=(r_ij) є симетричною.

Наприклад,

1.  

^,

2.  

^.

2 Матриця суміжності ребер графа

Нехай у графі m ребер. Матриця суміжності ребер неорієнтованого графа B=(b_ij) має розмір ,

де

Для орієнтованого графа

Наприклад,

1.  

^,

2.  

^.

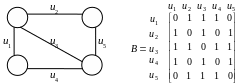3 Матриця інцидентності

Якщо граф неорієнтований і має n вершин і m ребер, то матриця інцидентності S=(s_ij) має розмір ,

де

Для орієнтованого графа

Наприклад,

1.  

^,

2.  

^.

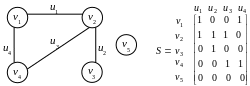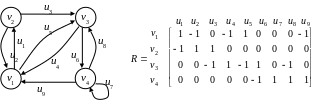За матрицею інцидентності можна відновлювати граф.

2.3 Дерева та ліс. Остовне дерево графа

Зв’язний граф без циклів називається деревом. Дерево графа має n–1 ребер, де n – кількість вершин. Ліс – це незв’язний граф без циклів.

Остовним називається дерево графа, що містить усі його вершини.

Існує спосіб підрахунку числа остовних дерев графа. Знайдемо матрицю R=(r_ij) – матрицю суміжності вершин графа. Далі утворюємо матрицю М за правилом: діагональні елементи матриці R замінюємо сумою елементів відповідного рядка, а елементи цього рядка, що дорівнюють «1», замінюємо на «-1». Можна довести, що алгебраїчне доповнення будь-якого елемента матриці М дорівнює числу остовних дерев даного графа.

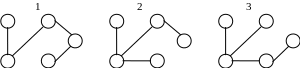
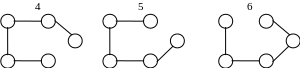
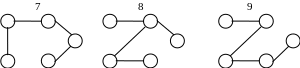
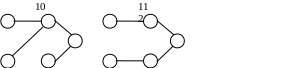
Приклад. Маємо граф

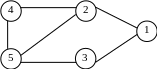
n=5 – кількість вершин графа

m=6 – кількість ребер.

Підрахуємо кількість остовних дерев графа

_.

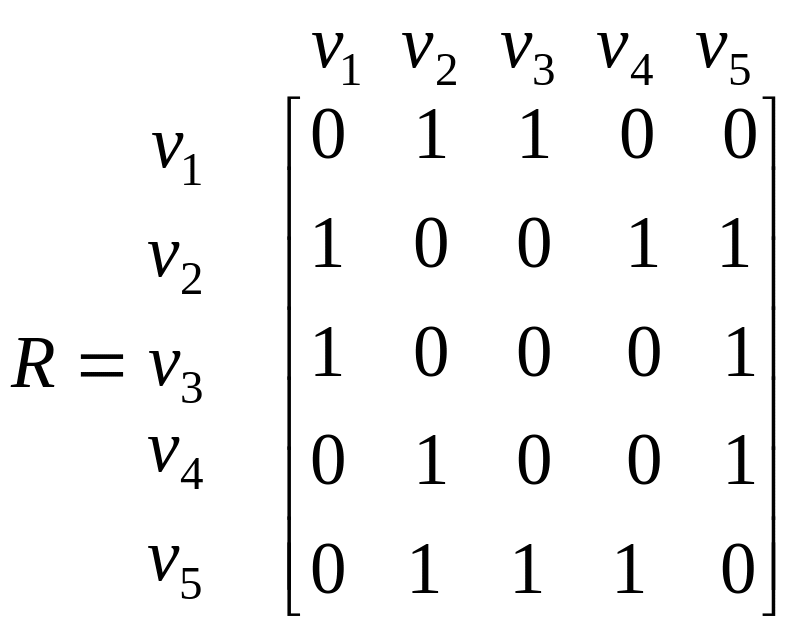Знайдемо матрицю М

_.

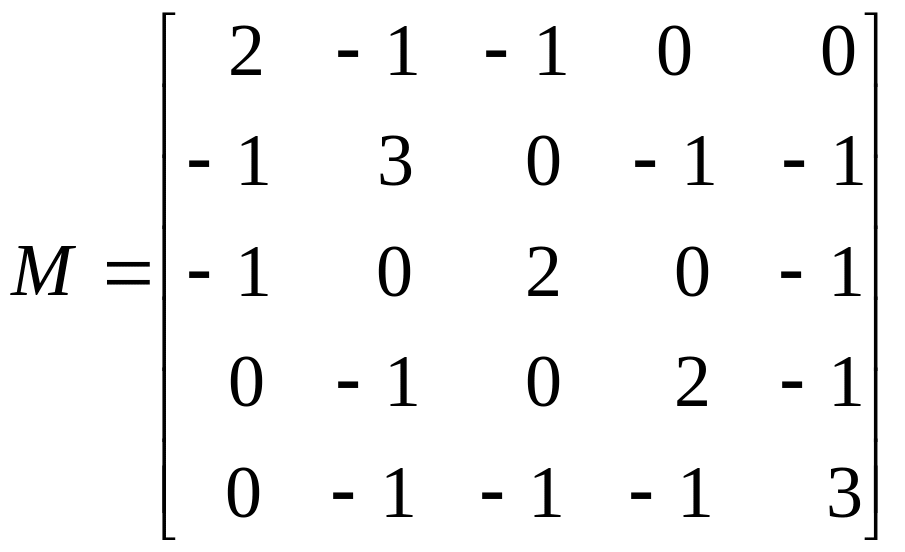Знайдемо алгебраїчне доповнення елемента m₁₁

_.

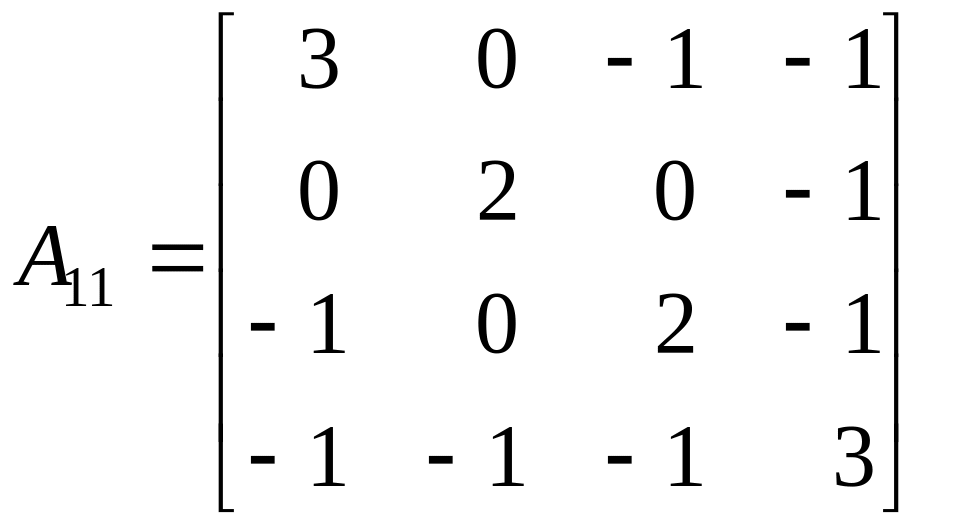Розкладемо визначник за елементами другого рядка

.

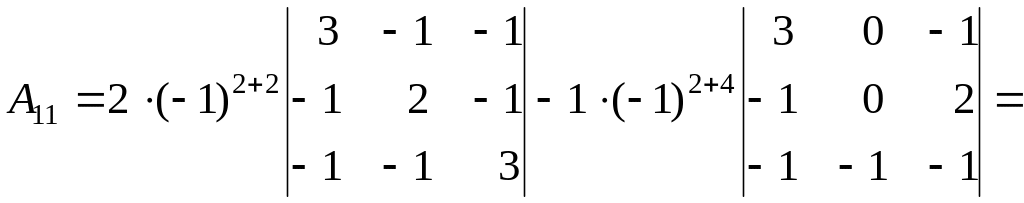
Даний граф має 11 остовних дерев.