5.2 Розв’язання гри у мішаних стратегіях

Якщо гра не має сідлової точки, то застосування чистих стратегій не дає оптимального розв’язку гри. В такому випадку одержати оптимальний розв’язок можна випадковим чином перебираючи чисті стратегії.

Мішаною стратегією S_А гравця А називається застосування чистих стратегій А₁, А₂,…, А_m з ймовірностями p₁, p₂,…, p_m. При цьому очевидно, що .

Мішані стратегії гравця А записують у вигляді матриці

,

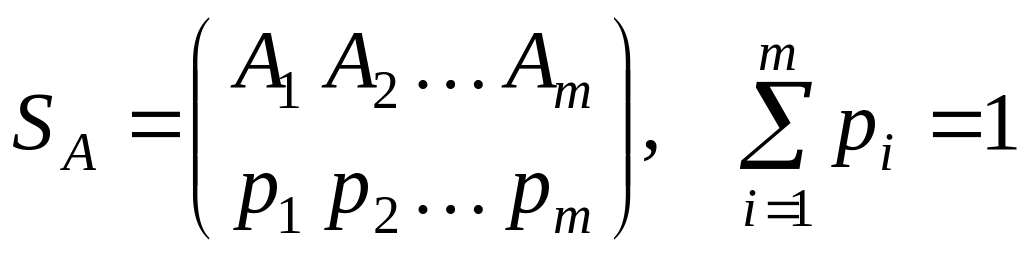або .

Аналогічно, мішані стратегії гравця В позначаються так:

,

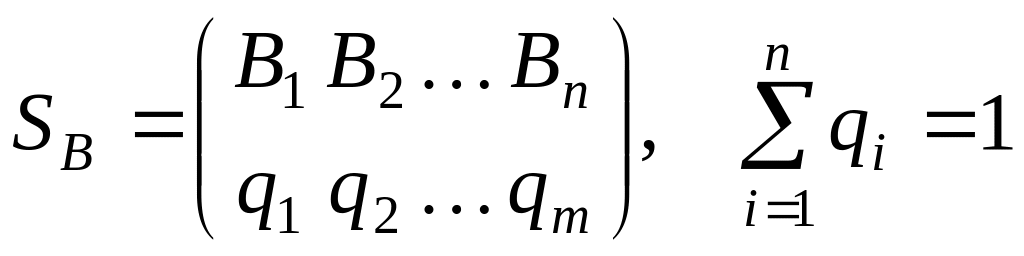або .

Чисті стратегії можна вважати окремим випадком мішаних у випадку, коли чистій стратегії відповідає ймовірність 1, а ймовірність інших стратегій дорівнює 0.

На основі принципу мінімакса визначається оптимальний розв’язок (або розв’язок) гри: це пара оптимальних стратегій , які мають наступні властивості: якщо один з гравців додержується своєї оптимальної стратегії, то іншому не може бути вигідним відходити від своєї. Виграш, що відповідає оптимальній стратегії (ціна гри v), задовольняє нерівності

 ≤ v ≤ .

Введемо в розгляд функцію виграшу

.

Гравець А орієнтується на найгірше, тобто на втрати, що дорівнюють мінімуму функції виграшу F(S_A,S_B) по всім стратегіям гравця В, тобто грає роль _i.

Тоді найкращою стратегією для гравця А є та, на якій буде досягнуто – це грає роль .

Аналогічно для гравця В найкращою стратегією буде та, на якій буде досягнуто – це грає роль .

Виникає питання: чи існують оптимальні мішані стратегії гравців , на яких гравець А має найбільший виграш і відповідно гравець В – найменший програш.

На це питання дає відповідь основна теорема теорії ігор – теорема Неймана.

Будь-яка матрична гра має ціну v в мішаних стратегіях, яка досягається у процесі використанні оптимальних мішаних стратегій , тобто

.

З цієї теореми випливають наступні висновки:

Теорема 1 Стратегії оптимальні тоді і тільки тоді, коли виконується умова

.

Тобто, якщо гравець В застосовує оптимальну стратегію , то кращою відповіддю на це є застосування гравцем А стратегії . І якщо гравець А застосовує оптимальну стратегію , то кращою відповіддю на це є застосування гравцем В стратегії .

Перш ніж сформулювати другу теорему, що випливає з основної теореми, дамо наступне означення.

Стратегії, які входять до складу оптимальних мішаних стратегій з ненульовими ймовірностями, називаються активними стратегіями.

Теорема 2 Якщо гравець В застосовує оптимальну мішану стратегію , а гравець А застосовує активну стратегію А_і, то . Аналогічно,

.

5.3 Ігри 2^x2

Така гра є найпростішим випадком гри. Якщо така гра має сідлову точку, то оптимальний розв’язок – це пара чистих стратегій, що відповідають цій точці.

Гра, в якій відсутня сідлова точка, відповідно до основної теореми теорії ігор, має оптимальний розв’язок, який визначається парою мішаних стратегій , .

Нехай платіжна матриця має вигляд

.

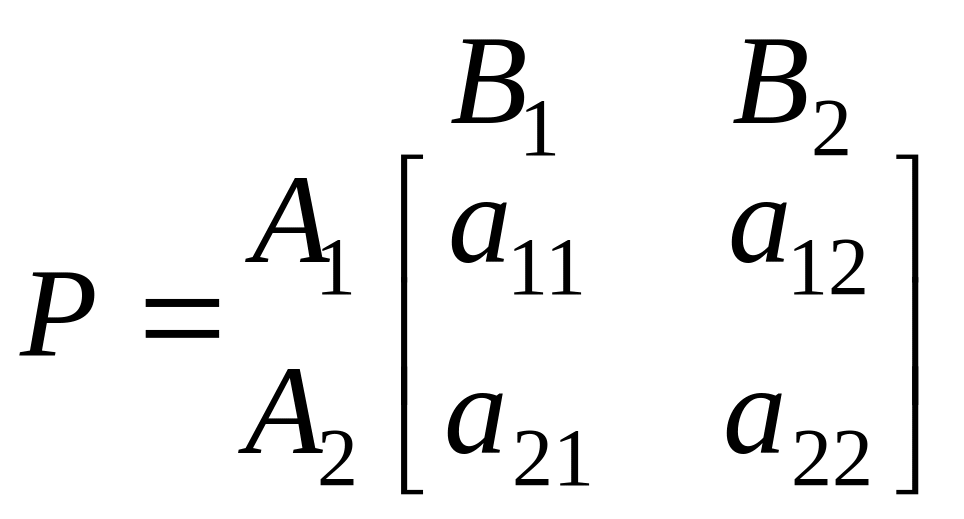Для того, щоб знайти оптимальні мішані стратегії , скористуємося теоремою 2.

,

.

Ми одержали систему рівнянь для визначення p^* і v. Аналогічним чином шукаємо стратегію :

.

Звідси вже можна знайти q^* і шукати вже не потрібно.

Приклад. Розв’язати гру «вірю – не вірю».

Правила цієї гри розглянуті в 6.1 і там же знайдена платіжна матриця цієї гри

.

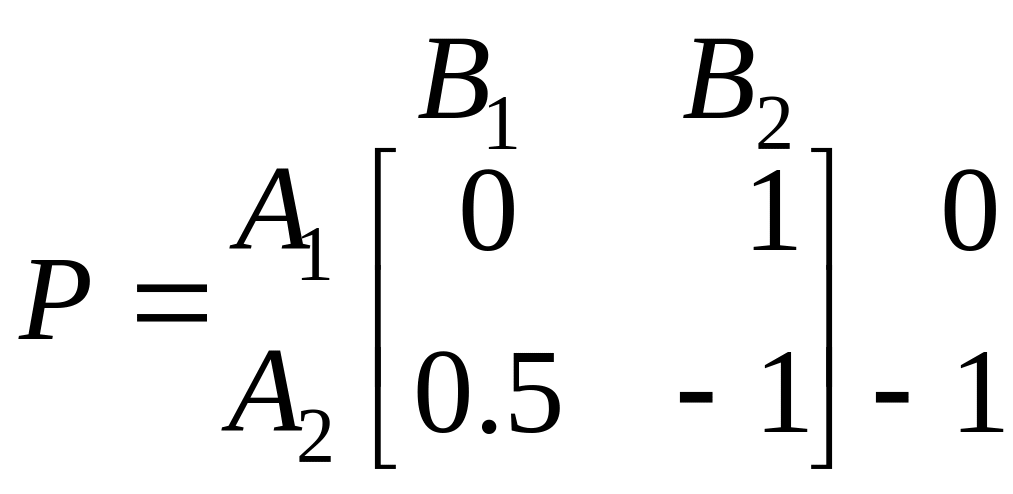Розв’язання. Оптимальні мішані стратегії гравця А – , гравця В – , =0, =1. Тоді

,

.

Розв’язуючи цю систему рівнянь, знаходимо

,

.

Тоді

.

Таким чином, оптимальні мішані стратегії гравців А і В такі:

.

Ціна гри дорівнює 0,2. Це означає, що гравець А в шести випадах з 10 має казати «правду», а в решті 4 – «неправду». Гравець В у восьми випадках з 10 має «вірити», а в решті – не вірити. Середній виграш в цій грі дорівнює

0,2 грн.