Интегрирование по частям
Интегрирование
по частям основано на представлении
подынтегрального выражения в виде
произведения 
и
последующем применении формулы 
.
Этот метод является очень мощным
инструментом интегрирования. В зависимости
от подынтегральной функции, метод
интегрирования по частям иногда
приходится применять несколько раз
подряд до получения результата. Для
примера найдем множество первообразных
функции арктангенс.
Пример.
Вычислить
неопределенный интеграл 
.
Решение.
Пусть 
,
тогда
Следует отметить, что при нахождении функции v(x) не прибавляют произвольную постоянную С.
Теперь
применяем формулу интегрирования по
частям:
Последний интеграл вычислим по методу подведения под знак дифференциала.
Так
как 
,
то 
.
Поэтому 
Следовательно,
где 
.
Ответ:
.
Основные трудности при интегрировании по частям порождает выбор: какую часть подынтегрального выражения брать за функцию u(x), а какую за дифференциал d(v(x)). Однако существует ряд стандартных рекомендаций, с которыми рекомендуем ознакомиться в разделе интегрирование по частям.
20. Определения и важнейшие свойства определенного интеграла
Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция илифункционал, а вторая — область в множестве задания этой функции (функционала).
Основные свойства интеграла. Установим ряд важных свойств определенного интеграла. Большая часть этих свойств присуща интегралам от любых интегрируемых функций, но мы будем формулировать их для функций непрерывных.
Теорема 1. Если f(x) и g(x) - две непрерывные функции, заданные на промежутке [a, b], то
т. е. интеграл суммы равен сумме интегралов слагаемых.
В самом деле, составляя интегральную сумму для функции f(x) + g(x), очевидно, будем иметь
после чего остается перейти к пределу при λ → 0.
Аналогично доказывается
Теорема 2. Если f(x) - непрерывная функция, а c - постоянное число, то
т. е. постоянный множитель можно выносить за знак интеграла.
Теорема 3. Пусть f(x) непрерывна на промежутке [a, b]. Если этот промежуток точкой c разложен на части [a, c] и [c, b], то интеграл по всему промежутку оказывается равным сумме интегралов по его частям, т. е.
В самом деле, будем при раздроблении промежутка [a, b] на части включать c в число точек деления. Если c = xm, то
Каждая из написанных здесь трех сумм является интегральной суммой соответственно для промежутков [a, b], [a, c] и [c, b]. Остается перейти к пределу при λ → 0.
21. Формула ньютона-лейбница
Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной.
-
Если непрерывна на отрезке
и 
—
ее любая первообразная на этом
отрезке, то имеет место равенство
Для
применения формулы Ньютона-Лейбница
нам достаточно знать одну из первообразных y
= F(x)подынтегральной
функции y
= f(x) на
отрезке [a;
b] и
вычислить приращение этой первообразной
на этом отрезке. В статье методы
интегрирования разобраны
основные способы нахождения первообразной.
Приведем несколько примеров для
разъяснения. Пример
.
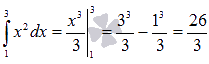22. Метод замены переменой в определенном интеграле
При вычислении определенных интегралов с использованием формулы Ньютона-Лейбница предпочтительно жестко не разграничивать этапы решения задачи (нахождение первообразной подынтегральной функции, нахождение приращения первообразной). Такой подход, использующий, в частности, формулы замены переменной и интегрирования по частям для определенного интеграла, обычно позволяет упростить запись решения.
ТЕОРЕМА.
Пусть функция φ(t) имеет непрерывную
производную на отрезке [α,β], а=φ(α), в=φ(β)
и функция f(х) непрерывна в каждой точке
х вида х=φ(t), где t
[α,β].
Тогда справедливо следующее равенство:
Эта формула носит название формулы замены переменной в определенном интеграле.
Подобно тому, как это было в случае неопределенного интеграла, использование замены переменной позволяет упростить интеграл, приблизив его к табличному (табличным). При этом в отличие от неопределенного интеграла в данном случае нет необходимости возвращаться к исходной переменной интегрирования. Достаточно лишь найти пределы интегрирования α и β по новой переменной t как решение относительно переменной t уравнений φ(t)=а и φ(t)=в. На практике, выполняя замену переменной, часто начинают с того, что указывают выражение t=ψ(х) новой переменной через старую. В этом случае нахождение пределов интегрирования по переменно Пусть f(z) - непрерывная функция, заданная на промежутке [p, q], а φ(x) - непрерывная функция, заданная на промежутке [a, b], имеющая там непрерывную же производную φ'(x) и удовлетворяющая неравенству p ≤ φ(x) ≤ q.
В таком случае
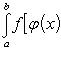
(22)
Формула (22) выражает собой правило замены переменной в определенном интеграле. Оно напоминает правило замены переменной в интеграле неопределенном, но отличается от него тем, что здесь отпадает надобность в возвращении к старой переменной, т. к. формула (22) представляет собой равенство двух постоянных чисел. Заметим еще, что эта формула заменяет собой для случая определенных интегралов оба вида правила подстановки в интегралах неопределенных; только, применяя ее на практике, иной раз приходится читать ее слева направо, а иногда - справа налево.
Переходя к доказательству теоремы, обозначим интегралы, входящие в левую и правую части формулы (22), соответственно через Iлев и Iправ.
23. Метод интегрирования по частям в определенном интеграле
Все выкладки статьи Интегрирование по частям в неопределенном интеграле в полной мере справедливы и для определенного интеграла. Плюсом идёт только одна деталь, в формуле интегрирования по частям добавляются пределы интегрирования:
Формулу
Ньютона-Лейбница здесь необходимо
применить дважды: для произведения 
и,
после того, как мы возьмем интеграл 
.
Тип интеграла для примера я опять подобрал такой, который еще нигде не встречался на сайте. Пример не самый простой, но очень и очень познавательный.
Пример 8
Вычислить
определенный интеграл
Решаем.
Интегрируем
по частям:
24. Матрицы
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы[1], в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.
Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.
Для матрицы определены следующие алгебраические операции:
сложение матриц, имеющих один и тот же размер;
умножение матриц подходящего размера (матрицу, имеющую
столбцов,
можно умножить справа на матрицу,
имеющую
строк);в том числе умножение на матрицу вектора (по обычному правилу матричного умножения; вектор является в этом смысле частным случаем матрицы);
умножение матрицы на элемент основного кольца или поля (то есть скаляр).
Относительно сложения матрицы образуют абелеву группу; если же рассматривать ещё и умножение на скаляр, то матрицы образуют модуль над соответствующим кольцом (векторное пространство над полем). Множество квадратных матриц замкнуто относительно матричного умножения, поэтому квадратные матрицы одного размера образуют ассоциативное кольцо с единицей относительно матричного сложения и матричного умножения.
Доказано, что каждому линейному оператору, действующему в n-мерном линейном пространстве, можно сопоставить единственную квадратную матрицу порядка n; и обратно — каждой квадратной матрице порядка n может быть сопоставлен единственный линейный оператор, действующий в этом пространстве.[2] Свойства матрицы соответствуют свойствам линейного оператора. В частности, собственные числа матрицы — это собственные числа оператора, отвечающие соответствующим собственным векторам.
То же можно сказать о представлении матрицами билинейный (квадратичных) форм.
В математике рассматривается множество различных типов и видов матриц. Таковы, например, единичная, симметричная, кососимметричная, верхнетреугольная (нижнетреугольная) и т. п. матрицы.
Особое значение в теории матриц занимают всевозможные нормальные формы, то есть канонический вид, к которому можно привести матрицу заменой координат. Наиболее важной (в теоретическом значении) и проработанной является теория жордановых нормальных форм. На практике, однако, используются такие нормальные формы, которые обладают дополнительными свойствами, например, устойчивостью.
Определение
Пусть
есть два конечных множества 
и 
,
где 
и
— натуральные
числа.
Назовём
матрицей размера 
(читается
на
)
с элементами из некоторого кольца или
поля 
отображение
вида
.
называется
элементом матрицы, находящимся на
пересечении 
-той
строки и 
-ого
столбца;
-ая строка матрицы состоит из элементов вида , где пробегает всё множество
;-ый столбец матрицы состоит из элементов вида , где пробегает всё множество
.
Если индекс пробегает множество , а пробегает множество , то совокупность элементов полностью определяет матрицу.
Таким образом, матрица размера состоит в точности из
строк (по элементов в каждом)
и столбцов (по элементов в каждом)
или
элементов.
В соответствии с этим
каждую строку матрицы можно интерпретировать как вектор в -мерном координатном пространстве
;каждый столбец матрицы — как вектор в -мерном координатном пространстве
.
Сама
матрица естественным образом
интерпретируется как вектор в
пространстве 
,
имеющем размерность
.
Это позволяет ввести покомпонентное
сложение матриц и умножение матрицы на
число (см. ниже); что касается матричного
умножения,
то оно существенным образом опирается
на прямоугольную структуру матрицы.
Если
у матрицы количество строк
совпадает
с количеством столбцов
,
то такая матрица называется квадратной,
а число 
называется размером квадратной
матрицы или её порядком.