1.Понятие функции вещественной переменной

2. Предел последовательности

В математике пределом последовательности элементов пространства называют элемент того же пространства, который обладает свойством «притягивать», в некотором смысле, элементы данной последовательности. Свойство последовательности, иметь или не иметь предел, называют сходимостью: если у последовательности есть предел, то говорят, что данная последовательность сходится, в противном случае (если у последовательности нет предела) говорят, что последовательность расходится. Понятие предела последовательности непосредственно связано с понятием предельной точки (множества): если у множества есть предельная точка, то существует последовательность элементов данного множества, сходящаяся к данной точке. Таким образом, у последовательности может быть несколько предельных точек, но, если последовательность сходится, то все предельные точки совпадают друг с другом и совпадают с пределом самой последовательности.

Определение

Пусть дано топологическое пространство   и последовательность   Тогда, если существует элемент   такой, что

,

где   — открытое множество, содержащее  , то он называется пределом последовательности  . Если пространство является метрическим, то предел можно определить с помощью метрики: если существует элемент   такой, что

,

где   — метрика, то   называется пределом  .

3. Свойства пределов

Обозначение предела Предел функции обозначается как   , при   или через символ предела   .

Всюду ниже предполагается, что пределы функций существуют.

Рассмотрим основные свойства пределов.

1. Предел суммы

Предел суммы равен сумме пределов, если каждый из них существует, т.е.

2. Предел разности

Предел разности равен разности пределов, если каждый из них существует, т.е.

3. Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

4. Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела:

5. Предел произведения Предел произведения равен произведению пределов, если каждый из них существует, т.е.

6. Предел частного

Предел частного равен частному пределов, если каждый из них существует и знаменатель не обращается в нуль, т.е.

7. Предел степенной функции

где степень p - действительное число.

8. Предел показательной функции

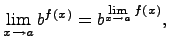
где основание b > 0.

9. Предел логарифмической функции

где основание b > 0.

10. Теорема "о двух милиционерах"

Предположим, что   для всех x близких к a, за исключением, быть может, самой точки x = a. Тогда, если

то

То есть функция f (x) остается "зажатой" между двумя другими функциями, стремящимися к одному и тому же пределу A.

4. Бесконечно малые и бесконечно большие последовательности

Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.

Последовательность   называется бесконечно малой, если  . Например, последовательность чисел   — бесконечно малая.

Функция называется бесконечно малой в окрестности точки  , если  .

Функция называется бесконечно малой на бесконечности, если   либо  .

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если  , то  ,  .

Свойства бесконечно малых

• Сумма конечного числа бесконечно малых — бесконечно малая.

• Произведение бесконечно малых — бесконечно малая.

• Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.

• Если   — бесконечно малая последовательность, сохраняющая знак, то   — бесконечно большая последовательность.

Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.

Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция  , неограниченная с обеих сторон, не является бесконечно большой при  .

Последовательность   называется бесконечно большой, если  .

Функция называется бесконечно большой в окрестности точки  , если  .

Функция называется бесконечно большой на бесконечности, если   либо  .