Дифференциальные уравнения первого порядка. Постановка задачи Коши. Рассмотрим дифференциальное уравнение первого порядка. Общий вид уравнения первого порядка
Если это уравнение разрешить относительно , то есть
(12)
то уравнение называется уравнением первого порядка, разрешенным относительно производной.
Определение 4. Общим решением дифференциального уравнения (12) называется дифференцируемая функция
(13)
которая зависит от одной произвольной постоянной С и обращает это уравнение в тождество.
Определение 5. Частным решением уравнения (12) называется решение, получаемое из общего решения (13) при каком-либо определенном значении произвольной постоянной С.
Рассмотрим дифференциальное уравнение первого порядка в симметричной относительно x и y форме:
(14)
При некоторых условиях уравнение (3) эквивалентно, по крайней мере, одному из дифференциальных уравнений вида:
Дифференциальное
уравнение
определяет в каждой точке (x,y), где
существует функция f(x,y), значение
то есть угловой коэффициент касательной
к интегральной кривой в этой точке.
Таким образом, дифференциальное уравнение
(12) определяет поле направлений.
Задачи интегрирования дифференциального уравнения заключаются в том, чтобы найти интегральные кривые, направления касательных к которым в каждой точке совпадают с направлением поля. Для построения интегральных кривых используют метод изоклин.
Определение 6. Изоклиной называется геометрическое место точек, в которых касательные к искомым интегральным кривым сохраняют постоянное направление.
Семейство изоклин дифференциального уравнения (12) определяется уравнением
, (15)
где K-параметр.
Постановка задачи Коши.
Задача о нахождении частного решения дифференциального уравнения, удовлетворяющего некоторым дополнительным условиям, часто встречается в приложениях. Если эти условия относятся к одному и тому же значению аргумента искомой функции, то их называют начальными. В том случае, когда начальные условия для дифференциального уравнения состоят в задании фиксированных значений функции и ее производных, их называют условиями Коши, а задачу – задачей Коши.
Задачей Коши для
дифференциального уравнения (12) называют
задачу нахождения решения
уравнения
удовлетворяющего начальному условию
(где
- заданные числа, называемые начальными
значениями или данными).
Геометрически это
означает, что ищется интегральная
кривая, проходящая через заданную точку
плоскости XOY.
Теорема. (о существовании и единственности решений задачи Коши.)
(без доказательства)
Пусть функция
и ее производные определены и непрерывны
на открытом множестве
.
Тогда в некоторой окрестности
точки
существует непрерывное решение
задачи Коши:
Замечание. Это
решение единственно, т.е. если
- два непрерывных решения задачи Коши,
то
для всех значений, при которых эти
решения определены.
Как известно, общее решение уравнения (12) задается следующим равенством
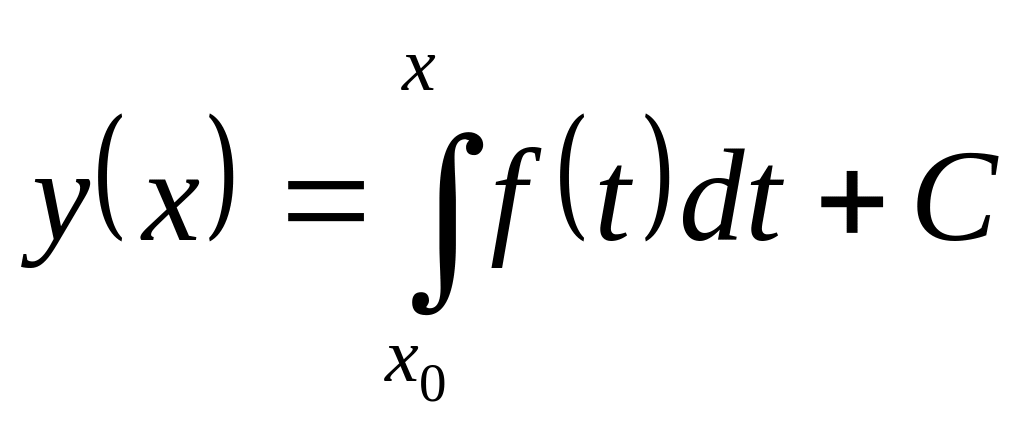(16)
Чтобы выделить
частное решение уравнения (12), достаточно
знать значение первообразной
в
какой – либо точке. Пусть, например,
Тогда из соотношения (16) имеем
или
,
т. е. решение единственно и равно
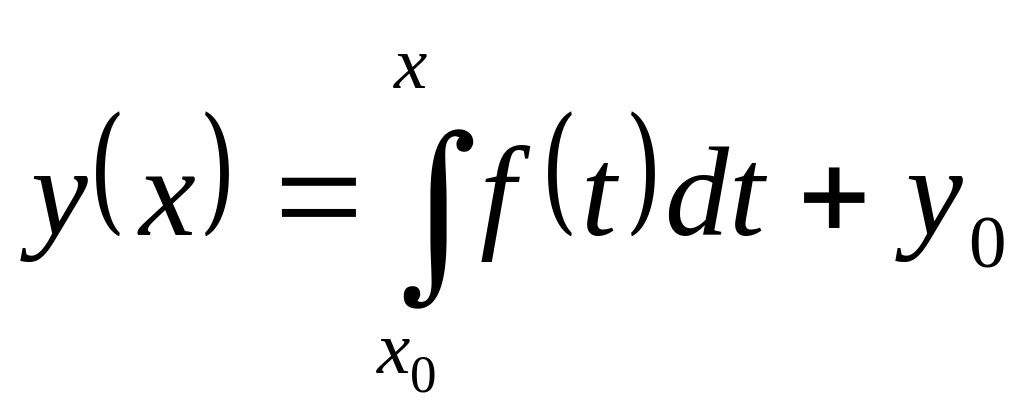(17)
Уравнение (17) называется частным решением задачи Коши.
Пример 3. Решить задачу Коши.
Решение. Согласно формуле (17) частное решение имеет вид
