§6. Свойства рациональных чисел

Свойство1: =[(a, b)], =[(c, d)], =[(m, n)]

Тогда имеют место следующие неравенства:

1. Если  > , то + > +

2. Если m > 0   > , то  > 

3. Если m < 0   > , то  < 

Док-во:

1. > => ad>bc

Док-ть: +>+

+ = [(an+bm, bn)]

+ = [(cn+dm, dn)]

(an+bm)dn > (cn+dm)bn

(an+bm)d > (cn+dm)b

and+bmd > cnb+dmb

and > cnd

ad > cb

3) m<0  ad>bc

Док-ть:  < 

 = [(am, bn)]

 = [(cm, dn)]

amdn < bncm

m < 0

ad > bc

Свойство2 (архимедовость поля рациональных чисел):

Док-во:

  0  > 0, n > 0

n > 0  

 > 0 a > 0 b > 0  

b  1

c(b)  c  

 > 0: n > 

Свойство3 (плотность множества рациональных чисел):

Множество рациональных чисел плотно, т. е. между произвольными неравными рациональными числами  и  существует по крайней мере одно рациональное число.

Док-во:

Пусть  >  находится между ними

+ > + > +

 > > 

§7. Представление рациональных чисел десятичными дробями

Определение: бесконечная десятичная дробь называется периодической, если существуют целые числа t  0, s  1, что n>t дроби a₀, a₁, a₂,…, a_n… a_n = a_n+s.

Наименьшее из таких s называется длиной периода.

Если t=0, то периодическая дробь называется чисто периодической. В этом случае период начинается сразу после запятой. t > 0, дробь называется смешанно периодической.

Теорема: пусть несократимая дробь. НОД(b, 10)=1. Тогда представляется в виде бесконечной десятичной дроби, длина периода которой равна порядку 10 по модулю b.

Док-во:

• a < b

(*)

• 

НОД(b, r_i )=1

• q_i<10

Из (*)

m 

• покажем, что дробь периодическая дробь. Каждое взаимнопросто с b, поэтому разные остатки принадлежать приведенной системе вычетов о модулю b, их  . Поэтому не позже чем через шагов остатки начнут повторяться.

Рассмотрим равенство (*) по модулю b:

(**)

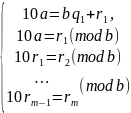Т.к. каждое r_i взаимнопросто с b, то можем сократить на

Если m – порядок числа 10 по mod b, т.е. , то

0< a< b, 0< r_m < b

• m соответствует наименьшему периоду

ОП: допустим r_l=a при l<m

Правило:

Чтобы записать чисто периодическую дробь в виде обыкновенной дроби, нужно период дроби записать в числителе, а в знаменателе записать столько 9 сколько цифр в периоде и полученную дробь добавить к целой части.

α=a₀, (a₁a₂…a_s)

Пример:

2, (435)=2+

Действительные числа

§1. Определение действительного числа.

Опр.1. Действительным числом называется , где

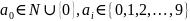
Выражение такого вида называется бесконечной десятичной дробью.

Десятичная дробь называется конечной, если начиная с какого-то места все цифры равны 0.

Опр.2. Десятичными числами называются бесконечные десятичные дроби кроме тех, в которых начиная с некоторого номера

Обозначение: - множество конечных десятичных дробей.

Опр.3. Две десятичные дроби называются равными, если: для действительных чисел

Опр.4. Будем говорить, что , если .