§2 Кватернионы.

Определение:

Алгеброй называется N-мерное векторное пространство над полем действительных чисел, если в нем однозначно определена и всегда выполняется операция умножения, ассоциативные, дистрибутивные относительно сложения и связанные с умножением элементов на действительные числа следующее равенств:

(kα)β=(αk)β=k(αβ), k ϵ R α, β ϵ A (A – алгебра)

Такая алгебра называется алгеброй ранга n.

Замечание:

Алгебра является кольцом. Это кольцо не всегда коммутативно.

Определение:

Если в алгебре ранга n выполнимо деление, то она называется телом (или алгеброй с делением ранга n).

Замечание:

Тело может быть не коммутативным.

Алгебра ранга n имеет некоторый базис 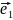, , 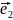…, . Элемент алгебры можно представить виде α = (a₁, a₂, …,a_n).

α = a₁ +a₂ +…+a_n

β = b₁ +b₂ +…+b_n

Умножение α∙β будет иметь вид 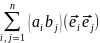выражено через всевозможные комбинации произведений базисных векторов.

Пример алгебры:

1. Поле действительных чисел R можно рассматривать как одномерное векторное пространство с одним базисным вектором:

n=1 =1

Любой элемент из R можно рассматривать как вектор α=α∙1. В этой алгебре выполнимо деление, поэтому R алгебра с делением ранга 1, причем коммутативная.

2. Поле комплексных чисел C:

n=2 =1, =i

Коммутативная алгебра с делением ранга.

3. Тело кватернионов H:

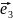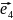n=4 =1, =i, =j, =k

	1	i	j	k
1	1	i	j	k
i	i	-1	k	-j
j	j	-k	-1	i
k	k	j	-i	-1

Пользуясь таблицей умножения можно найти произведение 2-х любых кватернионов.

q₁∙q₂=(a₁+b₁i+c₁j+d₁k)(a₂+b₂i+c₂j+d₂k)=

=a₁a₂+a₁b₂i+a₁c₂j+a₁d₂k+

+b₁ia₂+b₁ib₂i+b₁ic₂j+b₂id₂k+

+c₁ja₂+c₁jb₂i+c₁jc₃j+c₁jd₂k+

+d₁ka₂+d₁kb₂i+d₁kc₃j+d₁kd₂k=

=(a₁a₂-b₁b₂-c₁c₂-d₁d₂)+(a₁b₂+b₁a₂-d₁c₂+c₁d₂)i+(a₁c₂-b₁d₂+c₁a₂+d₁b₂)j+(a₁d₂+b₁c₂-c₁b₂+d₁a₂)k

Замечание:

Умножение коммутативно и это легко проверить: (q₁q₂)q₃=q₁(q₂q₃)

Алгебра H – есть алгебра с делением, т.е. тело (не коммутативное поле). Для этого достаточно убедиться, что в H содержится единица и любой другой кватернион не равный 0имеет обратный:

q≠0 q^-1: qq^-1=q^-1q=1

Определение:

Если q=a+bi+cj+dk, то число = a-bi-cj-dk называется сопряженным к числу q.

Найдем чему равно произведение q∙ = ∙q=a2+b2+c2+d2=N(q). N(q) называется нормой q. q≠0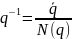

Замечание:

Нахождение частного от деления кватерниона q₁ на q≠0 сводится к решению двух (умножение не коммутативно) уравнений:

1. x∙q=q₁ – решается умножением обеих частей справа на q^-1

2. q∙y=q₁ – решается умножением обеих частей слева на q^-1

Пример:

Найти x из уравнения x∙q=q₁, если q=2+3i+j-5k, q₁=4+i-2j+3k

=2-3i-j+5k

N(q)=2²+3²+1²+(-5)²=39

x=q₁∙q-1=(4+i-2j+3k)∙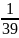 (2-3i-j+5k)=

Вывод:

Алгебра кватернионов H есть алгебра с делением ранга 4 над полем действительных чисел (или тело).

Утверждение:

Тело кватернионов H содержит поле комплексных чисел C

►q=a+bi+cj+dk →z=a+bi

Это соответствие взаимно-однозначно (биекция) и оно сохраняет операции сложения и умножения:

q₁=a₁+b₁i+0j+0k

q+q₁=(a+a₁)+(b+b₁)i+(c+0)j+(d+0)k

z+z₁= (a+a₁)+(b+b₁)i

qq₁=(aa₁-bb₁)+(ab₁+a₁b)i+0j+0k что соответствует

zz₁=(aa₁-bb₁)+(ab₁+a₁b)i

Таким образом, множество кватернионов вида q₁=a₁+b₁i+0j+0k изоморфно полю комплексных чисел, отсюда следует что тело кватернионов есть одно из расширений поля комплексных чисел. ◄

Теорема Фробениуса:

Алгебра с делением над полем действительных чисел является или полем действительных чисел или полем комплексных чисел или телом кватернионов.

Замечание:

Теорема устанавливает предел расширения числовых полей, а именно последним числовым полем, включающим все предшествующие числовые поля и кольца. Порядки их расширения являются телом кватернионов (не коммутативным).

Если же не требуется что бы числовая система была алгеброй с делением, то возможно построение сколько угодно гиперкомплексных систем или алгебр любого ранга, причем не только над R, но и над другими полями.

Например:

Над полем C можно построить алгебру B–кватернионов, так же как алгебру А кватернионов. Строится над полем R и имеет вид A+Bi+Cj+Dk. A, B,C, D ϵ С и 1, i, j, k – элементы базиса с той же таблицы умножения как в алгебре кватернионов, но алгебра B-кватернионов не обладает делением.