8

С.А. ЛАБУТИН

МЕТОДЫ РАСЧЕТА

МАГНИТНЫХ ПОЛЕЙ

НИЖНИЙ НОВГОРОД

2008

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ, НЕОБХОДИМЫЕ ДЛЯ РЕШЕНИЯ ЗАДАЧ

Магнитное поле в любой точке пространства можно описывать либо с помощью вектора напряженности магнитного поля , либо с помощью вектора магнитной индукции , которые в вакууме связаны соотношением: = ₀ , где ₀ = 1,26  10^–6 Гн/м – так называемая магнитная постоянная; в среде с магнитной проницаемостью  в рассматриваемой точке пространства эта связь принимает вид: = ₀ . При решении задач данного раздела следует воспользоваться либо законом полного тока, либо законом Био-Савара-Лапласа и принципом суперпозиции для напряженности магнитного поля.

1. Закон полного тока для токов проводимости (закон полного тока называется также теоремой о циркуляции напряженности магнитного поля):

Ц

–I

иркуляция вектора напряженности магнитного поля по замкнутому контуру L равна алгебраической сумме токов, охватываемых этим контуром, т.е. . Здесь I_k – только токи, охватываемые замкнутым контуром L, а - бесконечно малый элемент этого контура (рис. 1). Положительное направление этих векторных элементов (направление обхода контура) выбирается произвольно, но алгебраический знак токов уже зависит от этого выбранного направления. Токи, которые образуют с направлением обхода по контуру (направление вектора на рис. 1) правовинтовую систему, считаются положительными, в противном случае – отрицательными. Если токи текут во всем пространстве, где расположен контур, и задана плотность тока в каждой точке пространства, то протекающий через контур ток (т.е. ток, охватываемый контуром) находится с помощью интегрирования по всей поверхности S внутри контура, т.е. , где - положительная нормаль к площадке dS (т.е. нормаль, образующая с направлением обхода по контуру при вычислении циркуляции правовинтовую систему).

2. Отсутствие в природе магнитных зарядов приводит к тому, что линии вектора (или ) не имеют ни начала, ни конца, т.е. всегда являются замкнутыми. Поэтому поток вектора (или ) через любую замкнутую поверхность всегда равен нулю, т.е. интеграл по любой замкнутой поверхности S, где вектор направлен по нормали к этому элементу поверхности (для замкнутой поверхности положительным направлением нормали принято считать направление во внешнее пространство от этой поверхности)

3. З акон Био-Савара-Лапласа. Пусть по проводнику произвольной формы течет ток I (рис. 2). Выделим на этом проводнике бесконечно малый элемент проводника , направленный по касательной линии к проводнику в направлении тока I. Магнитная индукция , создаваемая этим элементом тока в некоторой точке А определяется по закону Био-Савара-Лапласа: , где - радиус-вектор, проведенный от элемента проводника в рассматриваемую точку поля А. Модуль вектора определяется выражением , где  - угол между векторами и .

4. Принцип суперпозиции для вектора (или ). Поле , порождаемое несколькими движущимися зарядами (токами), равно векторной сумме полей , порождаемых каждым зарядом (током) в отдельности: .

Применяя закон Био-Савара-Лапласа к проводникам различного вида, можно найти магнитные поля, создаваемые током, текущим по этому проводнику, и, в частности, получить следующие формулы:

1. Индукция магнитного поля, созданного отрезком прямого проводника с током, равна , где a - расстояние от исследуемой точки до линии, на которой расположен проводник; ₁ и ₂ - углы между радиусами-векторами, проведенными из концов проводника в исследуемую точку, и направлением тока.

1. Индукция магнитного поля на оси кругового тока 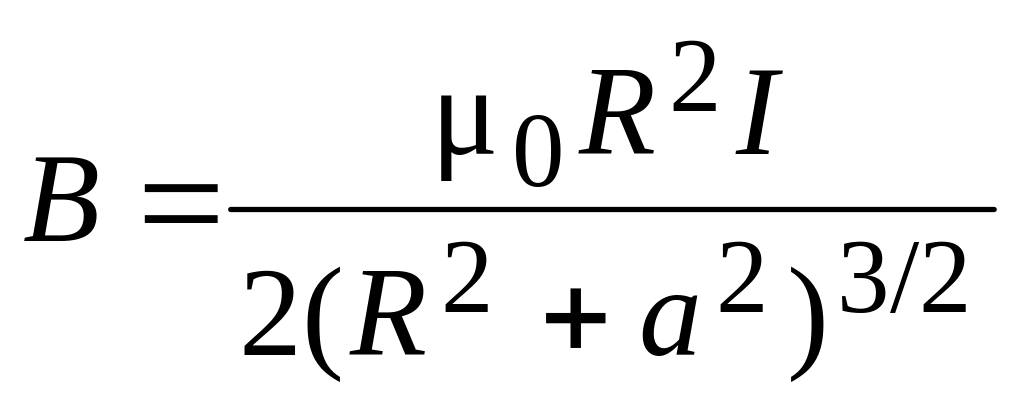, где R - радиус кругового контура с током; a - расстояние между исследуемой точкой на оси и центром контура с током. В центре контура с током (а = 0) получаем: .

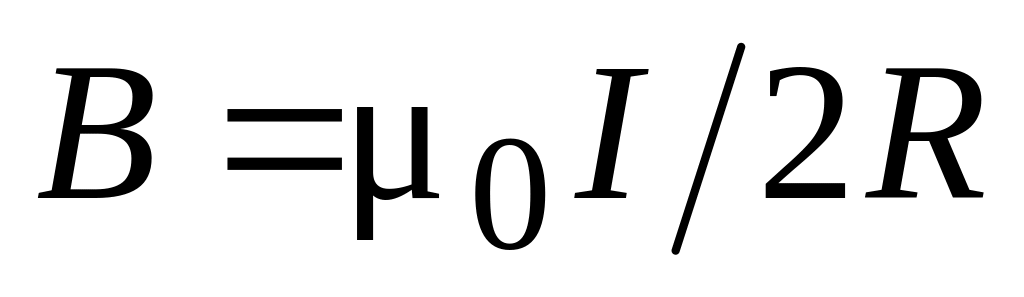1. Индукция магнитного поля на оси соленоида конечной длины, по проводнику которому течет току I, равна: , где ₁ и _{2 -} углы между осью соленоида и радиусами-векторами, проведенными из той точки на оси соленоида, в которой ищется поле, к концам соленоида, а n – число витков проводника соленоида на единице его длины. Если длина соленоида велика по сравнению с его диаметром, то последняя формула внутри такого соленоида далеко от его концов принимает приближенный вид 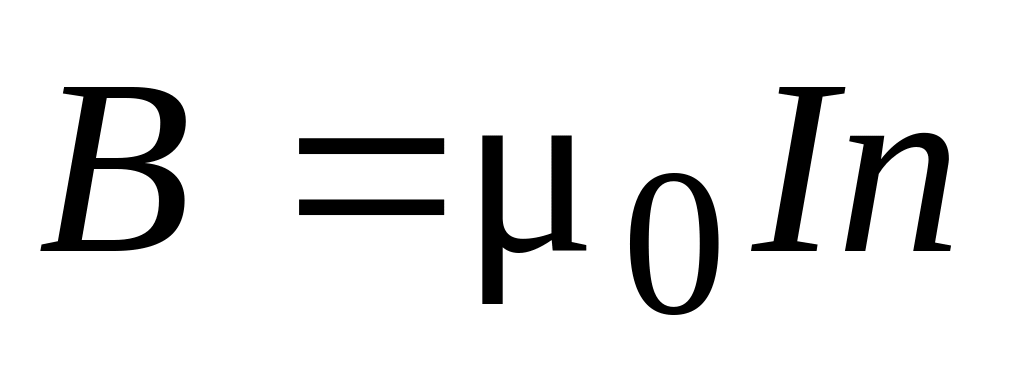. Точное равенство для последней формулы получается для соленоида бесконечной длины.

Расчет магнитных полей с помощью закона полного тока

Закон полного тока позволяет в ряде случаев найти напряженность магнитного поля более простым способом, чем с использованием закона Био-Савара-Лапласа и принципа суперпозиции магнитных полей. Однако число задач, решаемых с помощью закона полного тока, не слишком велико. С помощью этого закона можно найти поля внутри тороидальной катушке и бесконечно длинного соленоида; бесконечного прямолинейного тонкого проводника с током; бесконечного цилиндрического проводника с постоянной плотностью тока по сечению проводника или с плотностью тока, зависящему только от расстояния r от оси цилиндра; бесконечного цилиндрического слоя с постоянной плотностью тока по сечению слоя (или с плотностью тока, зависящему только от расстояния r от оси цилиндров); бесконечного по двум координатам плоского слоя с одинаковой плотностью тока , текущего внутри слоя параллельно одной из бесконечных поверхностей слоя (заметим, что во всех этих задачах в каждой точке пространства можно провести две взаимно перпендикулярные плоскости симметрии). В трех последних случаях проводники могут также содержать бесконечные цилиндрические полости произвольного радиуса (или полости в виде цилиндрического слоя), по которым ток не течет. Эти полости должны полностью лежать внутри рассматриваемого проводника с током.

Н иже рассмотрены некоторые задачи расчета магнитных полей с помощью закона полного тока.

Задача 1. Найти напряженность магнитного поля, создаваемого бесконечным прямым тонким проводником в точке А, удаленной на расстояние R от оси провода. По проводнику течет ток I (рис. 3).

Решение. Согласно закону Био-Савара-Лапласа направление магнитного поля всех элементов провода одинаково и направлено по касательному направлению к окружности, проведенной через точку, в которой ищется поле (рис. 3). Вдоль вертикального направления величина поля не должна изменяться (иначе будет нарушена исходная симметрия точек по вертикальному направлению). Одинаковой должна также оставаться величина поля (но не направление) в точках любой окружности, проведенной перпендикулярно проводнику, с центром на оси проводника (иначе будет нарушено исходное равноправие точек окружности по угловой координате). Следовательно, величина поля в любой точке пространства может зависеть только от расстояния R этой точки до проводника.

Для нахождения напряженности магнитного поля на расстоянии R от проводника с током запишем закон полного тока для окружности радиуса R (рис. 3): . Выберем направление обхода контура по направлению поля в точках этого контура (при этом положительным током проводника будет ток, текущий вниз). Поскольку в этом случае вектора и параллельны друг другу, то . При вычислении интеграла учтено, что величина поля Н зависит только от R и имеет вдоль окружности постоянное значение, что позволяет вынести эту величину за знак интеграла. Из последнего соотношения находим .

Задача 2. По сплошному цилиндрическому проводнику радиуса R течет ток с плотностью j. Найти напряженность магнитного поля внутри и вне проводника как функцию расстояния r от оси.

Решение. Из симметрии задачи следует, что поле Н может зависеть только от r, и в каждой точке пространства направлено по касательной к окружности с центром на оси цилиндра, проведенной через эту точку. Запишем закон полного тока для окружности внутри цилиндра и вынесем Н(r) за знак интеграла: . Таким образом, напряженность магнитного поля линейно растет от нуля на оси цилиндрического проводника до максимального значения на его поверхности. Вне цилиндра ток через контур в виде окружности будет равен jR². С учетом этого вне проводника с током из закона полного тока получаем: Н = jR²/2r, т.е. напряженность магнитного поля вне проводника постепенно уменьшается до нуля по гиперболическому закону.

Задача 3. По бесконечному слою толщиной 2d параллельно одной из поверхностей слоя течет ток с плотностью j. Найти напряженность магнитного поля как функцию расстояния х от плоскости симметрии слоя.

Решение. И з симметрии задачи следует, что магнитное поле лежит в плоскости симметрии, перпендикулярной слою, и проходящей через точку, где ищется поле; направлено перпендикулярно этой плоскости и зависит только от х. Найдем напряженность магнитного поля вне слоя. Выберем симметричный замкнутый контур в виде прямоугольника с расположением точки, где ищется поле, на одной из боковых сторон этого прямоугольника (верхний прямоугольник на рис. 4). Тогда на двух сторонах прямоугольника, перпендикулярных слою, имеем Н_l = 0. На двух других сторонах контура, находящихся вне слоя, поле Н_l = Н, имеет одинаковые значения в точках этих сторон и может быть вынесено за знак интеграла при расчете циркуляции. В результате имеем: . Отсюда получаем Н = jd, т.е. поле вне проводника имеет постоянное численное значение.

Если поле ищется внутри слоя, то для симметричного прямоугольного контура, проходящего через искомую точку внутри слоя (нижний прямоугольник на рис. 4), величина тока через этот контур равна j2xl. Циркуляция вектора Н остается без изменения и равна 2lH. Из закона полного тока находим, что внутри слоя поля растет линейно: Н = jх.

Задача 4. Найти поле внутри бесконечного соленоида с проводом, навитым на круглый цилиндрический каркас с плотностью витков n, если по проводу течет ток I.

Решение. Поле внутри такого соленоида параллельно оси соленоида и образует с направлением тока в витках правовинтовую систему. В учебнике И.В. Савельева "Курс общей физики". Том 2. (М.: Наука, 1988) на стр. 149-151 доказывается, что поле внутри бесконечного соленоида однородно, а вне соленоида – равно нулю. Тогда выбирая замкнутый контур в виде прямоугольника, две стороны которого параллельны оси соленоида (причем одна из этих сторон проходит через точку, в которой ищется поле, а другая сторона расположена вне соленоида) и две стороны – перпендикулярны этой оси (т.е. на этих двух сторонах Н_l = 0). Для этих двух сторон и для внешней стороны (в точках которой Н = 0) получаем . Следовательно, циркуляция по прямоугольному контуру равна Нl = lnI, где l– длина стороны прямоугольного контура внутри соленоида, направленной по его оси. Из полученного уравнения находим: Н = nI.

Произведение nI называется числом ампер-витков на метр. При n = 1000 витков на метр и силе тока в 1 А магнитная индукция В внутри соленоида составляет 4 10^–4 Тл.

З адача 5. На соленоид с полым картонным сердечником в виде тора с прямоугольным поперечным сечением (рис. 5) навита обмотка из N = 500 витков, обтекаемая током I = 2,4 А. Определить максимальное и минимальное значения индукции магнитного поля внутри тороида и магнитный поток системы, если R₁ = 5 см, R₂ = 8 см, b = 5 см.

Решение. Линии индукции внутри кольцевого соленоида (тороида), если витки его расположены вплотную, представляют собой окружности, концентричные самому тороиду. Благодаря этому поле может быть найдено с помощью закона полного тока.

Проведем контур L интегрирования в виде окружности радиуса r, концентричной кольцевому соленоиду. Тогда при правильном выборе направления обхода контура угол между векторами и равен нулю и косинус этого угла равен единице. Абсолютное значение вектора во всех точках контура будет постоянным и, следовательно, . Сумма токов, сцепленных с контуром L, в данном случае равна произведению силы тока в обмотке на число витков тока N в соленоиде, т.е. . Закон полного тока для вектора имеет вид . С учетом полученных выражений для правой и левой части этого выражения, получаем . Поскольку согласно условию задачи тороид не является тонким (разность R₂ – R₁ соизмерима с R₁), индукция магнитного поля в разных точках внутри сердечника будет различной. Наибольшего значения индукция В достигает при r = R₁; наименьшего значения – при r = R₂. Полагая  = 1 и подставляя численные значения заданных величин в полученную формулу для В, находим В_макс = 47,7 Тл и В_мин = 30 Тл.

Для нахождения магнитного потока площадь поперечного сечения тороида надо разбить на узкие элементарные площадки длиной b и толщиной dr. Тогда . Производя интегрирование и численный расчет, получаем .