5. Статистика заработной платы.

Задача. Имеются следующие данные о количестве рабочих и их заработной плате по предприятиям в двух отраслях.

Вычислить индексы средней заработной платы:

1. по каждой отрасли;

2. по двум отраслям;

а) индекс переменного состава;

б) индекс постоянного состава;

в) индекс структурных сдвигов.

Сделать выводы и объяснить полученные результаты.

Отрасль	Базисный период		Отчетный период
	Число работающих, чел	Средняя з/п, тыс. руб	Число работающих, чел	Средняя з/п, тыс. руб
1	150	900	140	1200
2	100	600	120	800

1. Определяем индивидуальный индекс средней заработной платы :

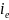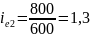
2. Рассчитываем индекс переменного состава :

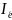3. Вычисляем индекс постоянного состава :

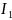4. Находим индекс структурных сдвигов :

Вывод:  Исследуя данные о количестве рабочих и их заработной плате по 2 отраслям можно сказать, что постоянный и переменный состав одинаковые, а структурный сдвиг равен 0,98.

6. Коэффициент Джинни и кривая Лоренца

Имеются следующие данные о распределении общего объема денежных доходов населения региона по 20% группам (в %).

Показатель	Значение
	Базисный	Отчетный
Денежные доходы всего, в том числе по 20% группам населения	100%	100%
1 группа (с наименьшим доходами	4	6
2 группа	8	10
3 группа	18	20
4 группа	30	30
5 группа (с наибольшими доходами)	40	34

1. Определить коэффициенты концентрации доходов Джинни.

2. Построить кривую Лоренца.

Год	Соц. группа населения	Доля населения,	Доля в общем объеме денежных доходов,	Сum		*Сum
базисный	1	0,2	0,04	0,04	0,008	0,008
	2	0,2	0,08	0,12	0,016	0,024
	3	0,2	0,18	0,3	0,036	0,06
	4	0,2	0,3	0,6	0,06	0,12
	5	0,2	0,4	1	0,08	0,2
	Итого	1	1	2,06	0,2	0,412
отчетный	1	0,2	0,06	0,06	0,012	0,012
	2	0,2	0,1	0,16	0,02	0,032
	3	0,2	0,2	0,36	0,04	0,072
	4	0,2	0,3	0,66	0,06	0,132
	5	0,2	0,34	1	0,068	0,2
	Итого	1	1	2,24	0,2	0,448

1. Определяем коэффициенты концентрации доходов Джинни.

Коэффициент Джинни: К = 1 – 2∑ x_i cum y_i + ∑ x_iy_i

К_баз. = 1 - 2 * 0,412 + 0.2 = 0,376

К_отч. = 1 – 2 * 0,448 + 0,2 = 0,304

Уменьшение коэффициента Джинни с 0,376 до 0,304 свидетельствует об усилении дифференциации доходов населения региона.

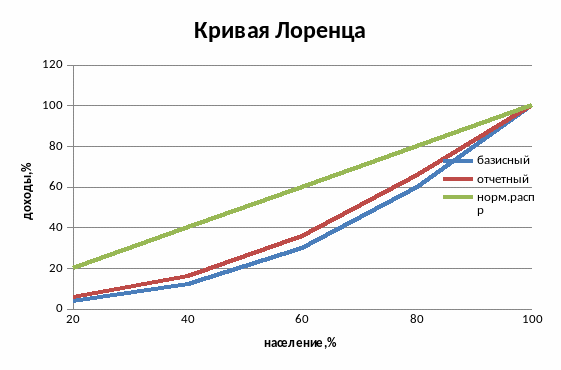
Кривая Лоренца иллюстрирует усиление неравномерности в распределении общего объема денежных доходов в отчетном году по сравнению с базисным.