- •Раздел 3.
- •Тема 8. Смещения равновесий двух фаз в многокомпонентных системах.
- •8.1. Изобарическое смещение равновесия жидкость-пар.
- •8.1.1. Общий случай равновесия: каждый компонент присутствует в каждой фазе.
- •8.1.2. Частный случай равновесия: раствор. В-ва ж. Фазы отсутствует в п. Фазе из-за
- •8.2. Изотермическое смещение равновесия жидкость-пар.
- •8.2.1. Общий случай равновесия: каждый компонент присутствует в каждой фазе.
- •8.2.2. Частный случай равновесия: раствор. В-ва ж. Фазы отсутствует в п. Фазе из-за
- •8.3. Изобарическое смещение равновесия твёрдое – жидкость.
- •8.3.1. Общий случай: каждый компонент присутствует в каждой фазе.
- •8.3.2. Частный случай равновесия: т. Фаза содержит лишь чистый компонент k.
8.2. Изотермическое смещение равновесия жидкость-пар.
8.2.1. Общий случай равновесия: каждый компонент присутствует в каждой фазе.
1. Особенности системы: |
||
1) ,
2)
3)
испарение конденсация
компонента k
4)NЗСФР = К(ж, п) (А-1) = К(2-1) = К.
|
||
2. Дифф. форма ЗСФР |
||
Аналит. выражение
Исследование
т.к.
|
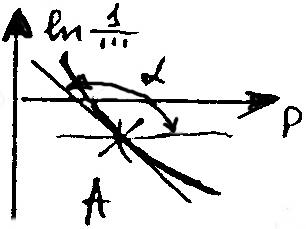
Граф. образ функции
Возможные расчёты: определение
|
|
3. Интегр. форма ЗСФР |
||
Аналит. выражение
2)
Исследование
|
Граф. образ
функции
Возможные расчёты: 1) Определение или по остальным; 2) Определение или по остальным; 3) Определение р по остальным; 4)
Определение
|
|
4. Применение рk-шкалы в п. фазе. |
||
– функция р при
зад. Т
– const
при заданной Т |
||
5. приближение идеал. растворов для обеих фаз. Законы Рауля и Генри. |
||
Вариант 1. |
Вариант 2. |
|
1) п.
фаза близка к ид. газ. р-ру 2)
ж. фаза близка к соверш.р-ру
Решение относительно
Определение р Возможные расчёты: 1) Определение по остальным; 2)
Определение
3)
Определение
|
1) п. фаза близка к ид. газ. р-ру ; 2)
ж. фаза близка к ид.р-ру в узком понимании
Решение относительно
Возможные расчёты: 1)
Определение
2)
Определение
3)
Определение
|
|
8.2.2. Частный случай равновесия: раствор. В-ва ж. Фазы отсутствует в п. Фазе из-за
их нелетучести. Понижение давления насыщенного пара растворителя.
1. Особенности системы: |
||||
1(ж) и 1(п) s(ж) 1) =
* 2)
|
3
испарение конденсация
компонента k
4)NЗСФР = К(ж, п) (А-1) = 1(2-1) = 1. |
|||
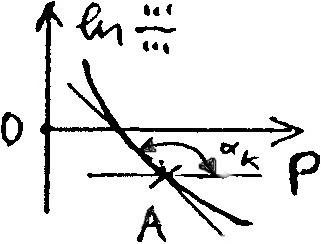
2. Дифф. форма ЗСФР для компонента 1 – растворитель ж. фазы. |
||||
Аналит. выражение
Исследование
|
Граф. образ
функции
Возможные расчёты: определение по tg α1 графически |
|||
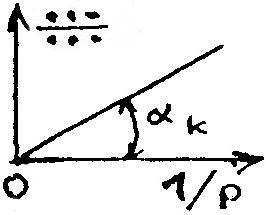
3. Интегр. форма ЗСФР для компонента 1 – растворитель ж. фазы. |
||||
Аналит. выражение в приближениях: 1)
2)
2) Решение относительно р
Исследование:
|
Граф. образ функции
из-за присутствия в ней нелетучих раствор. веществ s.
В 1) Определение по остальным; 2)
Определение
3) Определение р по остальным; 4)
Определение
|
|||
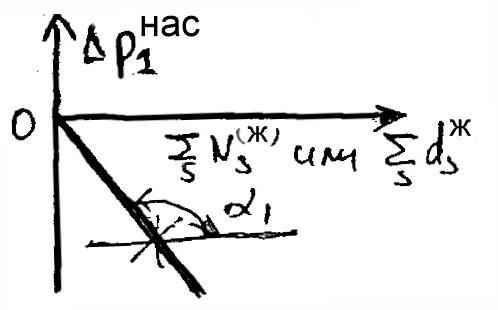
4. Линейные законы понижения давления нас. пара р-ля ж. фазы. |
||||
Формирование
2 ) ж. фаза – идеал. раствор: =1
– линейные законы понижения давления нас. пара р-ля ж. фазы в N- и d-шкалах. |
Граф. образы лин. законов:
Возможные расчёты: 1)
Определение
2)
Определение
3) Определение по остальным. |
|||




 1)
1)



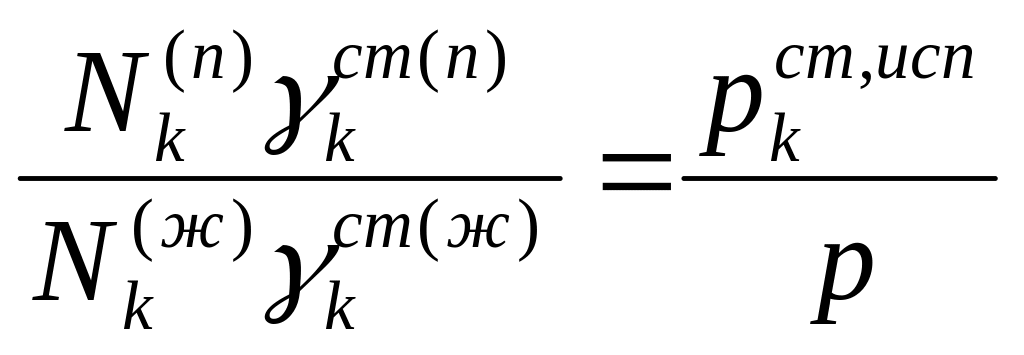

 (для
всех k)
(для
всех k) ,
,
 (для всех s)
(для всех s)
 )
)





 1)
1)

 озможные
расчёты:
озможные
расчёты: 1 ) ж. фаза
– разбавленный раствор:
1 ) ж. фаза
– разбавленный раствор: