Умовне позначення часу

Рік	1989	1990	1991	1992	1993	1994	1995	1996
Рівень	-7	-5	-3	-1	+1	+3	+5	+7

_{За непарної кількості членів ряду відлік ведеться від середини, яку приймають за нуль. Значення за парної кількості рівнів}

_{за непарної}

_{Приклад. За даними таблиці 7 знайти рівняння динаміки}

_{Р і ш е н н я. Розраховуємо параметри ti, ti}²_{, yi і вносимо в табл.7.}

_{Таблиця 7}

Розрахунок значення для визначення рівняння динаміки

Рік	Процент забруднення від рівня ГДК (Y)	ti	ti2	yi	Теоретичне значення yi
1	2	3	4	5	6
1987	39,4	-9	81	-354,6	39,29
1988	39,8	-7	49	-278,6	39,73
1989	40,0	-5	25	-200,0	40,17
1990	40,6	-3	9	-121,8	40,61
1991	41,4	-1	1	-41,4	41,05
1992	41,9	+1	1	41,9	41,49
1993	41,9	+3	9	125,7	41,93
1994	42,0	+5	25	213,0	42,37
1995	42,6	+7	49	300,2	42,81
1996	43,1	+9	81	387,9	43,25
Сума	412,7	0	330	72,3	412,70

_{З таблиці знаходимо: при n=10}

_{Тоді рівняння прямої буде мати вигляд}

_{За отриманим рівнянням знаходимо теоретичне значення проценту забруднення повітря від рівня ГДК для кожного періоду часу.}

_{Мірою коливання рівнів динамічного ряду є середній квадрат відхилень фактичних рівнів ряду від змінних рівнів, які обчислюються за трендом. Ця величина подібна дисперсії, яка обчислюється в рядах розподілу з певною відмінністю – відлік відхилень ведеться не від середньої (сталої для певного ряду), а від змінної середньої – вирівняних рівнянь. Міра коливання визначається за формулою}

_{Для тренду (див. табл.7), вираженого прямою yt =41,27+0,22t ,міра коливання буде дорівнювати:}

_{Відносна міра коливання (своєрідний коефіцієнт варіації) визначається за формулами}

_{для нашого прикладу}

_{а у відсотках . Величина служить критерієм вірності вибору рівняння тренду.}

_{Сезонні коливання параметрів екологічних процесів. Велика кількість екологічних процесів змінюють свій характер в залежності від зміни сезонів року. Такі зміни викликають сезонні коливання тих чи інших параметрів цих процесів. Вивчення сезонних коливань має самостійне значення як дослідження особливого типу динаміки.}

_{Сезонність можна розуміти як загальну динаміку всередині року. Моделлю рівнів, які періодично змінюються, служить ряд Фур’є, аналітичне вираження якого можна застосовувати до динаміки. Воно має вигляд}

_{В цьому рівнянні величина k визначає номер гармоніки ряду Фур’є і може бути взятою з необхідним ступенем точності ( найчастіше від 1 до 4 ). Параметри рівняння визначаються методом МНК за формулою}

_{Для вивчення специфічного періодичного явища сезонності беремо n=12 (кількість місяців року), а ряд динаміки можна записати у вигляді , показаному у табл.8.}

_{Таблиця 8}

Ряди динаміки для виявлення сезонних коливань

0
y0	y1	y2	y3	y4	y5	y6	y7	y8	y9	y10	y11

_{При розрахунку приймається до уваги те , що в чотирьох квадратах від 0 до 2π косинуси та синуси чотири рази приймають одні й тіж значення; 0; 0,5; 0,866; і 1, взяті із знаком мінус або плюс.}

_{Приклад. Розглянемо модель сезонності для даних, які наведені в табл.9.}

_{Таблиця 9}

_{Дані про рівні, які помісячно} періодично змінюються

Місяць	t	y	cos t	sin t	y cos t	y sin t	yt
1	0	39,8	1,000	0,000	39,80	0,00	44,17
2		62,2	0,866	0,500	53,86	31,10	93,70
3		125,5	0,500	0,866	62,95	109,03	152,13
4		256,2	0,000	1,000	0,00	256,20	205,81
5		271,1	-0,500	0,866	138,05	239,10	234,88
6		155,7	-0,866	0,500	-221,44	127,85	237,04
7		177,6	-1,000	0,000	-177,60	0,00	168,31
8		144,0	-0,866	-0,500	-124,70	122,00	160,16
9		86,7	-0,500	-0,866	-46,35	-75,08	129,87
10		52,8	0,000	-1,000	0,00	52,80	88,49
11		38,3	0,500	-0,866	19,15	-33,17	18,97
12		37,9	-0,866	-0,500	32,82	-18,95	16,82
Сума	–	1553,2	–	–	-496,56	461,28	1552,9

_{Р і ш е н н я. Знаходимо cos t, sin t, y cos t, y sin t і визначаємо}

_{Тоді рівняння сезонної моделі буде мати вид}

_{Індексом сезонності називається відношення середньої з фактичних рівнів однойменних місяців до середньої з вирівняних даних по тим самим місяцям}

_.

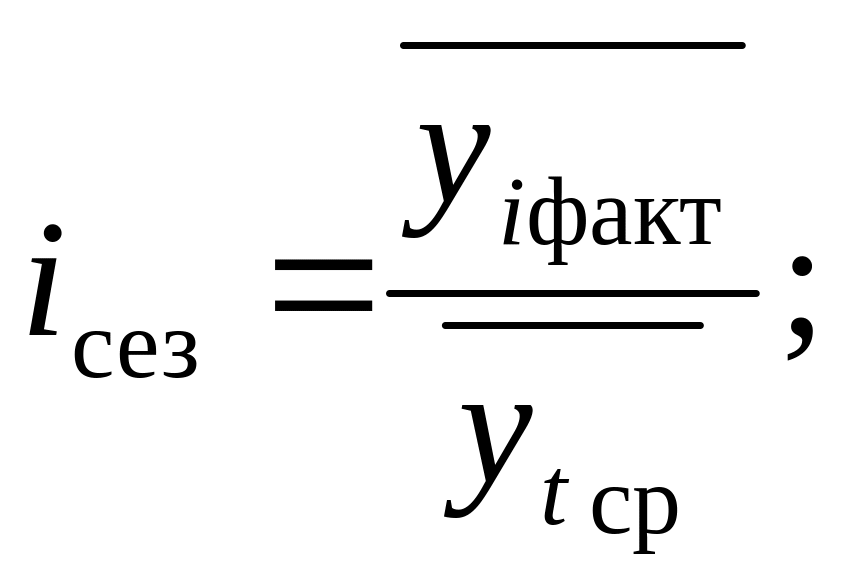
_{Отже, величина iсез різна для кожного місяця і залежить від способу вирівнювання, який може бути виконаним або із застосуванням дванадцятимісячної ковзної середньої, або аналітичним вирівнюванням.}

_{Показником сили коливання динамічного ряду через сезонний характер процесу служить середнє квадратичне відхилення індексів сезонності (виражається в процентах) від 100%}

_{Порівняння середніх квадратичних відхилень, які розраховуються за два періода, показують зрушення в сезонності. Якщо величине σсез зменшується, то сезонний характер досліджуваного явища йде на спад.}

_{Вивчення глибини сезонних коливань можливо і шляхом визначення відношень відхилення фактичних рівнів від вирівняних до теоретичних відхилень, прийняті за «норму».}

_{Деякі способи виміру розмаху сезонної хвилі засновані на вивченні не абсолютних відхилень фактичних даних від вирівняних, а відхилень з урахуванням знаку.}