Основные свойства пределов

1. Функция не может иметь более одного предела (при одной и той же базе).

2. Предел постоянной равен самой этой постоянной: , с – постоянная.

3. Предел суммы функций равен сумме пределов этих функций:

4. Предел произведения функций равен произведению пределов этих функций:

Отсюда следует, что постоянный множитель можно выносить за знак предела:

5. Предел частного двух функций равен частному пределов этих функций (если предел делителя не равен нулю):

6. (свойство предела сложной функции) Если , то предел сложной функции .

7. Если при базе В (т.е. в некоторой окрестности точки х₀ или при достаточно больших х) f₁(х) < f₂(х), то .

Отметим, что в перечисленных свойствах предполагается существование пределов функций f₁(х) и f₂(х), из чего следуют заключения о значениях пределов суммы, произведения или частного этих функций. Но при этом из существования предела суммы, произведения или частного функций не обязательно следует, что существуют пределы самих слагаемых, сомножителей или делимого и делителя.

Например, , но при этом не существует.

Замечательные пределы

Для вычисления пределов функций в некоторых случаях удобно использовать так называемые замечательные пределы (здесь рассматриваются без доказательства).

Первый замечательный предел

Второй замечательный предел

Для числовой последовательности (1 + 1/n)ⁿ:

Число е (число Эйлера) – это иррациональное число, которое приблизительно равно 2,718281. Это число широко используется в математическом анализе. График функции у = е^х называют экспонентой³. Логарифм по основанию е называют натуральным и обозначают ln x.

Можно доказать, что для функций f(x) = (1 + 1/x)^x и f(x) = (1 + x)^1/x:

Непрерывность функции

Функция f(x) называется непрерывной в точке x₀, если она удовлетворяет трем условиям:

1) определена в точке (т.е. существует f(x₀));

2) имеет конечный предел при хх₀;

3) этот предел равен значению функции в точке х₀,

т.е. .

Поясним определение непрерывности следующим примером (рисунок 2.10). На рисунке представлены графики четырех функций y = f(x), первые три из которых не являются непрерывными в точке x = 0, а четвертая – является.

В самом деле, функция (а) не является непрерывной в точке x = 0, так как вообще не определена в этой точке (т.е. нарушено первое условие непрерывности).

Д

Рисунок 2.10 – Иллюстрация к определению непрерывности функции

ля функции (б) в точке x = 0 первое условие непрерывности выполняется, но нарушается второе условие – отсутствует предел функции в этой точке (существуют только односторонние пределы, не равные друг другу: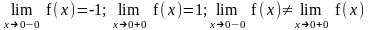 ). Поэтому функция (б) также не является непрерывной.

Для функции (в) в точке x = 0 выполняются первые два условия непрерывности, но при этом , а f(0) = 1. Так как , нарушается третье условие непрерывности, и эта функция также не является непрерывной.

А вот функция (г) в точке x = 0 является непрерывной, так как в этом случае выполняются все три условия непрерывности: .

По-другому вышеприведенное определение непрерывности функции можно записать в виде: (для непрерывной функции возможна перестановка символов предела и функции).

Слово «непрерывность» применительно к функции используется в связи с тем, что если функция непрерывна в точке, то ее график в этой точке можно провести, не отрываясь от листа, т.е. сам график непрерывен.

Если функция не является непрерывной в точке х₀, то эту точку называют точкой разрыва функции.

Точки разрыва могут быть первого и второго рода.

В точке разрыва первого рода либо существуют конечные односторонние пределы функции слева и справа, не равные друг другу (как на рисунке 2.10 (б)), либо предел функции в этой точке существует, но не равен значению функции в этой точке (как на рисунке 2.10 (в)). В последнем случае точку разрыва первого рода называют точкой устранимого разрыва.

В точке разрыва второго рода хотя бы один из односторонних пределов равен бесконечности или не существует (как на рисунке 2.10 (а), где односторонние пределы равны бесконечности).

Непрерывность функции в точке можно определить и по-другому.

Функция у = f(х) называется непрерывной в точке х₀, если она определена в эnой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции: .

Под приращением функции здесь будем понимать разность между значением функции при значении аргумента, увеличенном на приращение x, и ее значением в точке x₀: y = f(x₀ + x) - f(x₀) (рисунок 2.11).

Можно доказать эквивалентность этих двух определений непрерывности.

Рисунок 2.11 – Приращение аргумента и приращение функции