Средняя гармоническая:

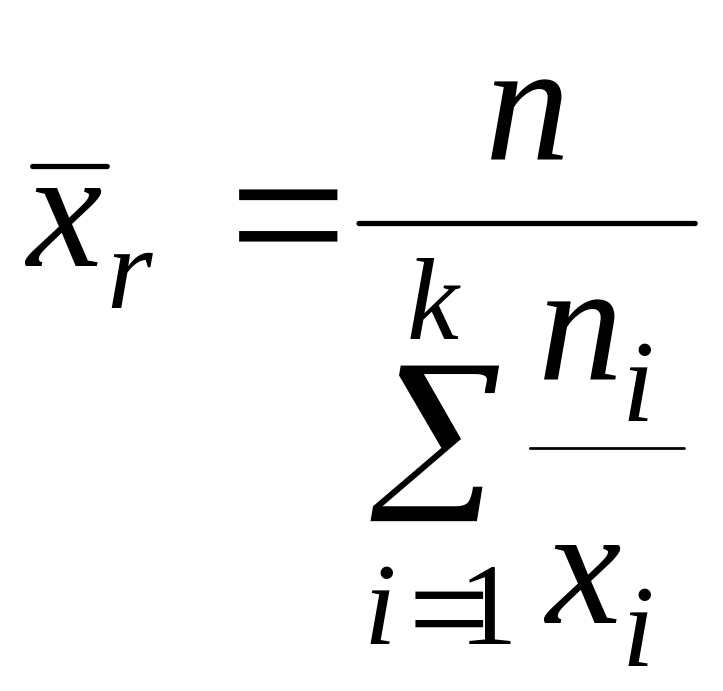(10)

Эта величина применяется, когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение, т.е. произведения по каждому признаку равны.

Средняя квадратическая:

(11)

Средняя геометрическая:

(12)

Этой средней удобно пользоваться, когда уделяется внимание не абсолютным разностям, а отношениям двух чисел, т.е. индивидуальные значения признака – относительные величины. Она используется в расчётах среднегодовых темпов роста, а также для определения равноудалённой величины от максимального и минимального значений признака.

Необходимо заметить, что разные виды средних величин при одном и том же исходном материале имеют неодинаковое значение:

(13)

Эти неравенства называются мажорантностью средних.

Для характеристики структуры совокупности применяются особые показатели, которые называются структурными средними. К ним относятся мода и медиана.

Выборочная мода ( ) - это варианта, имеющая наибольшую частоту или то значение признака, которое соответствует максимальной точке теоретической кривой распределения.

Выборочная медиана ( ) – это варианта, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечётное, т.е. , то ; при чётном , .

Если , , совпадают, то данное распределение симметрично.

Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называют вариацией признака, которую характеризуют следующие показатели:

Выборочная дисперсия ( ) - это среднее арифметическое квадратов отклонений наблюдаемых значений от выборочного среднего:

(14)

Мерой надёжности средней является выборочное среднее квадратическое отклонение ( ).

= (15)

Чем меньше , тем лучше отражает собой всю представленную совокупность.

Коэффициент вариации (V) - это выраженное в процентах отношение выборочного среднего квадратического отклонения к выборочной средней. Он служит для сравнения величин рассеяния двух вариационных рядов. Ряд, у которого коэффициент вариации больше, имеет большее рассеяние:

V=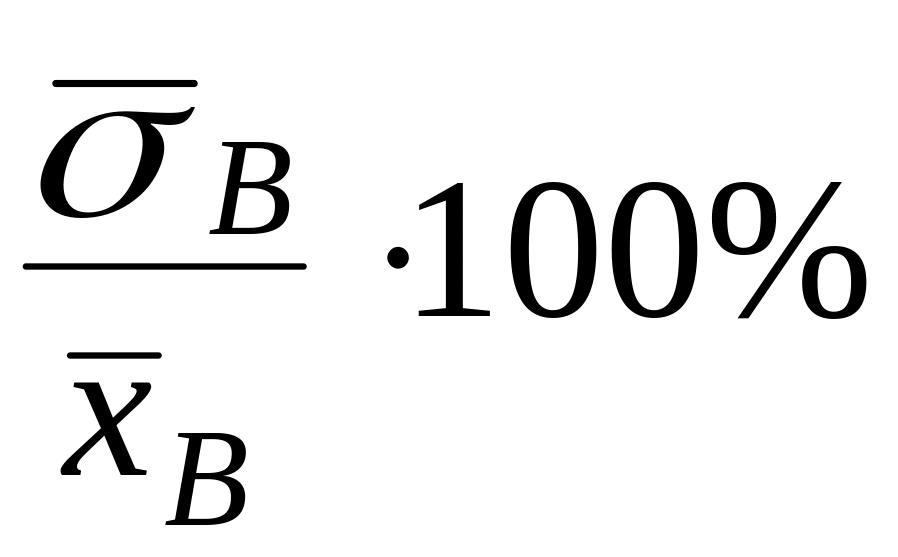 (16)

Если V33%, то имеет место большая колеблемость изучаемого признака.

Для характеристики колеблемости признака используется ряд показателей. Наиболее простой - размах варьирования (R). Это разность между наибольшей и наименьшей вариантами:

R= (17)

Чтобы дать обобщающую характеристику распределению отклонений, исчисляют среднее абсолютное отклонение ( ). Это среднее арифметическое абсолютных отклонений:

(18)

служит для характеристики рассеяния вариационного ряда и учитывает различия всех единиц изучаемой совокупности.

Величины , , имеют такие же свойства как M[x], D[x], σ[x].

Выборочная средняя является несмещённой состоятельной оценкой для М[x], а в случае нормального закона – эффективной. Выборочная дисперсия - смещённая оценка для D[x]; - смещённая оценка для σ[x].

Для устранения смещённости выборочной дисперсии и среднего квадратического отклонения их умножают на дроби и соответственно. В результате «исправленная» дисперсия и «исправленное» среднее квадратическое отклонение соответственно равны:

и (19)

Оценки , , , S являются состоятельными, но не эффективными.

Все оценки, рассмотренные выше – точечные. Они выражаются одним числом. При выборке малого объёма точечная оценка может значительно отличаться от оцениваемого параметра, то есть могут возникнуть грубые ошибки.

Задача интервального оценивания состоит в том, чтобы по данным выборки найти такой интервал, который с заданной вероятностью покрывает оцениваемый параметр.

< < (20)

Заданную вероятность называют надёжностью (доверительной вероятностью). Она задаётся наперёд, причём в качестве берут число, близкое к единице (0,95;0,99;0,999), а точность берут равной 0,1; 0,01; 0,001, в зависимости от задачи.

Интервал ( ) называют доверительным. Именно он покрывает неизвестный параметр с заданной надёжностью .

Пусть генеральная совокупность распределена по нормальному закону, причём известно. Требуется построить доверительный интервал для математического ожидания. В качестве точечной оценки параметров нормального закона возьмём , = .

Вероятность заданного отклонения вычисляется по формуле:

где t= , и тогда

или

P( -t Ф(t)= (21)

Для заданного по таблице функции Лапласа (Приложение 4) определяют квантиль t для функции Ф(t).

Квантилью, или левосторонней критической областью, отвечающей вероятности , называется такая граница, левее которой вероятность равна . Квантиль обозначается по определению , т.е. квантиль является решением уравнения .

Доверительный интервал для оценки среднего квадратического отклонения случайной величины Х с надёжностью для нормального закона распределения случайной величины находится из неравенств [1]:

, (22)

где S – несмещённое значение выборочного среднего квадратичного отклонения;

q – параметр, который находится по таблице (Приложение 5) на основе известного объёма выборки n и заданной надёжности оценки .

С помощью рядов распределения решается важнейшая задача статистики – характеристика закономерностей и изменение показателей колеблемости для варьирующих признаков. Определение формы кривой распределения является важной задачей, так как обрабатываемый материал даёт по определённому признаку характерную, типичную для него кривую. Всякое искажение формы кривой означает нарушение или изменение нормальных условий возникновения материала.

Для характеристики распределений используются моменты распределения. Это средние величины отклонений определённой степени от какого-либо числа. Если это средние арифметические, то моменты называются центральными. Если отклонения отсчитываются от произвольно выбранного начала, то они называются условными. Если же это число равно 0, то моменты распределения называются начальными.

Центральный эмпирический момент k-го порядка случайной величины Х вычисляется по формуле:

(23)

Наиболее точным и распространённым показателем является асимметрия ( ). Это отношение центрального эмпирического момента третьего порядка к кубу среднего квадратического отклонения. Она характеризует несимметричность распределения случайной величины.

(24)

Асимметрия положительна, если «длинная часть» кривой распределения расположена справа от математического ожидания и отрицательна, если «длинная часть» кривой расположена слева от математического ожидания.

Оценка степени существенности этого показателя даётся с помощью средней квадратической ошибки, которая зависит от объёма наблюдений n и рассчитывается по формуле:

(25)

если отношение 3, то асимметрия существенна, а если 3, то её наличие может быть объяснено влиянием различных обстоятельств.

Для оценки «крутости», то есть большего или меньшего подъёма кривой распределения по сравнению с нормальной кривой, пользуются другой характеристикой - эксцессом.