27. Коэффициент ассоциации Юла, его вероятностная интерпретация

Вероятность того, что 2 случайных объекта относятся к гомогенным категориям признаков (Х₁ и У₁ или Х₂ и У₂) на Q больше, чем к гетерогенным.

28. Коэффициент коллигации, его свойства.

Для всех ячеек рассчитывается так же.

Свойства:

1. Y=0, если признаки независимы, т.е. D=0

2. Принимает значение +1, когда =0, то есть в случае полной связанности; принимает значение -1, когда =0, то есть в случае полной отрицательной связанности.

3. Удовлетворяют принципу инвариантности Юла.

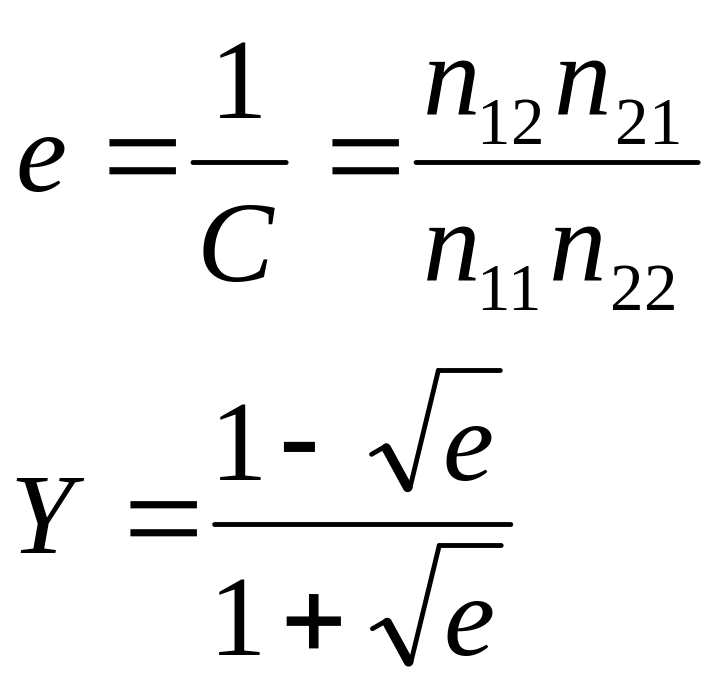
Связь между X и Y полная, если все Х₁ являются одновременно Y₁, несмотря на то, что не все Y₁ являются одновременно Х₁. Если все Х₁ являются одновременно Y₁ и все Y₁ являются одновременно Х₁, то связь абсолютная. Коэффициент коллигации характеризует полную связь.

Границы доверительного интервала:

- точечная оценка коэффициента коллигации

- оценка стандартной ошибки коэффициента.

29. Коэффициент коллигации, его вероятностная интерпретация.

- вероятность предсказать принадлежность к категории 2-го признака, если знаем принадлежность к категории 1-го признака

- вероятность предсказать принадлежность к категории 1-го признака, если знаем принадлежность к категории 2-го признака

- вероятность ошибки классификации одного из признаков при известной категории другого.

Если знаем категорию Y и надо предсказать категорию Х:

Если принадлежит к B,тогда вероятность предсказать

Если принадлежит к , тогда вероятность предсказать

По формуле Байеса:

Если знаем категорию X и надо предсказать Y:

- вероятность ошибки неправильной классификации по одному из признаков при неизвестной категории другого.

λ показывает, насколько снизится ошибка предсказания одного из признаков у случайно отобранного объекта при наличии информации о том, к какой категории другого признака он принадлежит, в сравнении с ситуацией, когда эта информация отсутствует.

а)

По принципу инвариантности Юла:

а)

Точно так же =Y.

В общем случае =|Y|. Таким образом, у У такая же вероятностная интерпретация, как и у .

30. Коэффициент контингенции, его свойства.

Для всех ячеек рассчитывается так же.

Свойства:

1. V=0, если признаки независимы, т.е. D=0

2. V растёт, если D растёт

3. V=-1, если одна обе гомогенные частоты нулевые и V=1, если обе гетерогенные частоты нулевые.

Связь между X и Y полная, если все Х₁ являются одновременно Y₁, несмотря на то, что не все Y₁ являются одновременно Х₁. Если все Х₁ являются одновременно Y₁ и все Y₁ являются одновременно Х₁, то связь абсолютная. Коэффициент контингенции характеризует абсолютную связь.

Границы доверительного интервала:

- точечная оценка коэффициента коллигации

- оценка стандартной ошибки коэффициента.

31. Коэффициент Гудмена-Краскала λa, его свойства, вероятностная интерпретация и интервальные оценки (таблицы rХs).

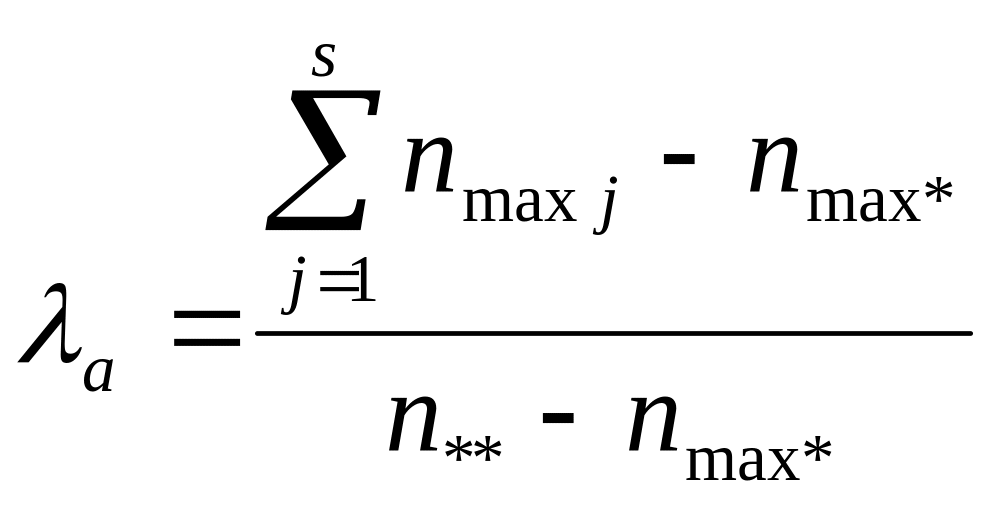
где ;

Если , то существует однозначная или взаимооднозначная зависимость Х от У., т.е. Х жестко связан с У или связан по вероятности.

Если , то Х не зависит от У, т.е. информация об У не улучшит прогноза Х, а также когда все максимальные значения наблюдаемых частот по столбцам находятся в одной строке, соответствующей максимальной маргинальной частоте, что является главным недостатком коэффициента.

Вероятностный смысл – показывает снижение вероятности ошибки предсказания признака Х при известной информации о принадлежности наблюдения к некоторому классу признака У по сравнению с ситуацией, когда информация отсутствует.

Интервальная оценка:

где - сумма только таких максимальных элементов столбцов, для которых значение j обеспечивает попадание в строку с наибольшим итогом