|
|
График
1.3.7.1.
Эта
функция непрерывна в точке A и разрывна
в точке B
|
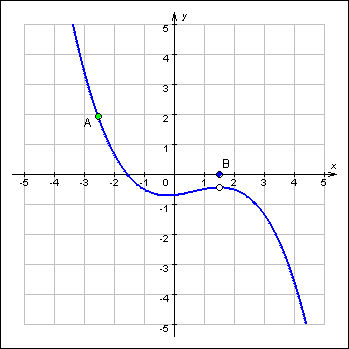
График
1.3.7.2.
На
рисунке показана функция 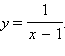 Она
разрывна в точке x0 = 1,
так как не существует в этой точке.
Она
разрывна в точке x0 = 1,
так как не существует в этой точке.
|
Примером
разрывной функции может служить функция
зависимости плотности воды в окрестности
0 ºC. Примером непрерывной функции
является зависимость площади квадрата
от длины его стороны. Подчеркнем еще
раз, что непрерывность функции
рассматривается только на области ее
определения.
Если
функция непрерывна в каждой точке
некоторого промежутка, то она называется
непрерывной на этом промежутке.
Большинство функций, изучаемых в
элементарной математике, непрерывны
на всей области определения. Таковыми
являются линейная функция y = kx + b,
квадратичная y = ax2 + bx + c,показательная и тригонометрические функции.
Если
функции f (x) и g (x) непрерывны
в точке x0,
то их сумма и произведение также
непрерывны в этой точке, а функция 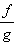 непрерывна
в ней при условии, чтоg (x0) ≠ 0.
непрерывна
в ней при условии, чтоg (x0) ≠ 0.
Отсюда
следует, что рациональные функции
непрерывны во всех тех точках, в которых
их знаменатель не обращается в нуль.
Из
непрерывности функции y = f (x) в
точке x0 и
функции z = g (y) в
точке y = f (x0) следует
непрерывность сложной функции g (f (x)) в
точке x0.
Функцию f (x) называют непрерывной
на отрезке [a; b],
если она непрерывна в каждой точке
интервала (a; b) и,
кроме того, непрерывна справа в точке a и
слева в точке b.
Т еорема
Вейерштрасса. Если
функция f (x) непрерывна
на отрезке [a; b],
то она ограничена на этом отрезке и
достигает своего наибольшего и
наименьшего значения.
еорема
Вейерштрасса. Если
функция f (x) непрерывна
на отрезке [a; b],
то она ограничена на этом отрезке и
достигает своего наибольшего и
наименьшего значения.

|
Рисунок
1.3.7.1.
Теорема
Коши о нулях непрерывной функции.
Только на одном из отрезков – [a3; b3] –
имеется нуль функции, так как на
этом отрезке функция непрерывна и
принимает значения разных знаков на
концах
|
Т
еорема
Коши. Если
функция f (x) непрерывна
на отрезке [a; b]
и принимает на его концах значения
разных знаков, то на отрезке [a; b]
имеется хотя бы один нуль функции f.
При этом, если функция строго монотонна
на этом отрезке, то она принимает
значение 0 лишь один раз.
Т
еорема
о промежуточных значениях. Если
функция f (x) непрерывна
на отрезке [a; b]
и f (a) ≠ f (b),
то для каждого значения y,
заключенного между f (a) и f (b),
найдется точка 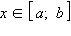 (и
возможно, не одна) такая, что f (x) = y.
(и
возможно, не одна) такая, что f (x) = y.
8)Вопрос
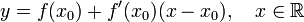 .
.
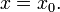
Нормаль —
это прямая, ортогональная (перпендикулярная)
касательному пространству (касательной
прямой к кривой, касательной
плоскости к поверхности и т. д.).
Вектор
нормали к
поверхности в данной точке — это
единичный вектор,
приложенный к данной точке и параллельный
направлению нормали. Для каждой точки
гладкой поверхности можно задать два
нормальных вектора, отличающихся
направлением. Если на поверхности можно
задать непрерывное поле нормальных
векторов, то говорят, что это поле
задает ориентацию поверхности
(то есть выделяет одну из сторон). Если
этого сделать нельзя, поверхность
называется неориентируемой.
Аналогично
определяется вектор
нормали к
кривой в данной точке. Очевидно, что к
кривой к данной точке можно приложить
бесконечно много не параллельных
векторов нормали (аналогично тому, как
к поверхности можно приложить бесконечно
много не параллельных касательных
векторов). Среди них выбирают два,
ортогональных друг к другу: вектор
главной нормали, и вектор бинормали.
9)Вопрос Производные и дифференциалы высших порядков
Пусть
производная некоторой функции f дифференцируема.
Тогда производная от производной этой
функции называется второй
производнойфункции f и
обозначается f".
Таким образом,
f"(x)
= (f'(x))'.
Если
дифференцируема (n -
1)-я производная функции f,
то ее n-й
производной называется
производная от (n -
1)-й производной функции f и
обозначается f(n).
Итак,
f(n)(x)
= (f(n-1)(x))', n ϵ N, f(0)(x)
= f(x).
Число n называется порядком
производной.
Дифференциалом n-го
порядка функции f называется
дифференциал от дифференциала (n -
1)-го порядка этой же функции. Таким
образом,
dnf(x)
= d(dn-1f(x)), d0f(x)
= f(x), n ϵ N.
Если x -
независимая переменная, то
dx =
const и d2x = d3x =
... = dnx =
0.
В
этом случае справедлива формула
dnf(x)
= f(n)(x)(dx)n.
Справедливы
формулы
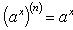
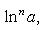
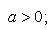
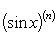
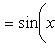
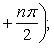
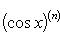
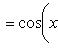
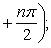
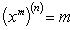
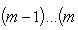
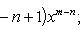
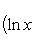
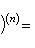

Формула
Лейбница
Если u и v - n-кратно
дифференцируемые функции, то
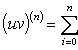
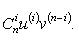
Производные n-го
порядка вектор-функции, комплекснозначной
и матричной функций
Если
компоненты 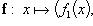
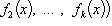 n-кратно
дифференцируемы, то
n-кратно
дифференцируемы, то 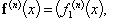
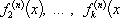
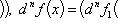
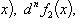
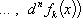 .
.
Аналогично
для комплекснозначной функции f и
матричной функции A имеем
формулы:
f(n)(x)
= u(n)(x)
+ iv(n)(x); dnf(x)
= dnu(x)
+ idnv(x);
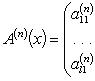
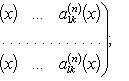
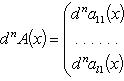
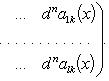
10)вопрос
Основные теоремы дифференциального
исчисления
10.1.1.
Теорема Ферма
Пусть
функция 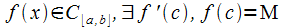 или
или 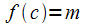 в
т.
в
т.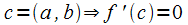 ■
■
□ Пусть,
для определённости,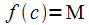 (рис.
10.1), тогда
(рис.
10.1), тогда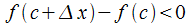 при
при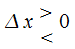 и
и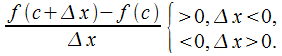
Согласно
определению производной имеем
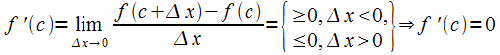 ◙
◙
Рис.
10.1
Геометрическое
истолкование теоремы вытекает из
геометрического смысла производной:
касательная к графику функции 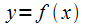 в
точке с абсциссой
в
точке с абсциссой параллельна
оси
параллельна
оси .
.
10.1.2.
Теорема Ролля
Пусть
функция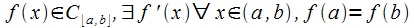 .
Тогда
.
Тогда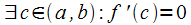 ■
■
□ Из
условия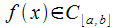 следует
по свойству 10 непрерывных
на
следует
по свойству 10 непрерывных
на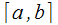 функций,
что
функций,
что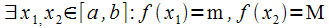 .
.
Существует
две возможности:
1) 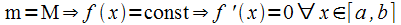 ;
;
2) 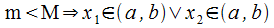 в
силу
в
силу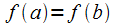 .
.
Пусть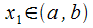 ,
тогда согласно теореме Ферма
,
тогда согласно теореме Ферма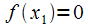 .
.
Данная
теорема обладает таким же геометрическим
истолкованием, что и теорема Ферма.
10.1.3.
Теорема Лагранжа
Пусть
функция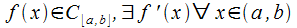 .
Тогда
.
Тогда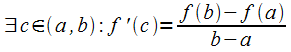 ■
■
□ Введём
на
вспомогательную
функцию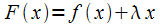 ,
для которой верны условия теоремы
Ролля:
,
для которой верны условия теоремы
Ролля: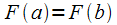 или
или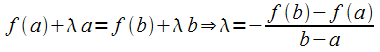 .
.
Следовательно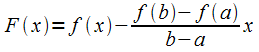 .
.
Солгасно
т. Ролля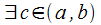 :
:
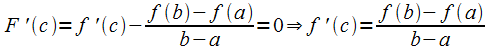 ◙
◙
Геометрическое
истолкование теоремы Лагранжа. Строим
график функции
(рис.
10.2), 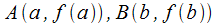 .
Угловой коэффициент касательной в
т.
.
Угловой коэффициент касательной в
т. 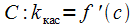 .
Следовательно, на графике функции
.
Следовательно, на графике функции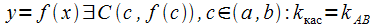 .
.
10.1.4.
Теорема Коши
Пусть
функции
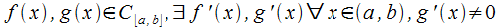 .
Тогда
.
Тогда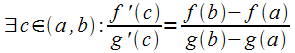 ■
■
В
формуле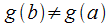 .
В противном случае согласно теореме
Ролля
.
В противном случае согласно теореме
Ролля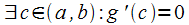 .
.
□ Введём 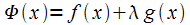 .
Подберём такое
.
Подберём такое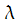 ,
чтобы
,
чтобы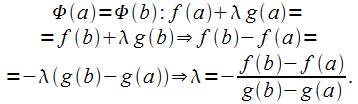
Тогда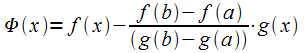 .
По теореме Ролля
.
По теореме Ролля 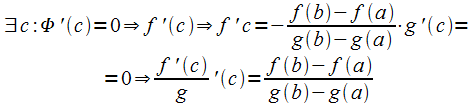 .
.
Теорема
Коши является обобщением теоремы
Лагранжа, где 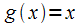 .
.
11)Вопрос
Правило
Лопиталя (теорема Вернули – Лопиталя).
Пусть 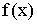 и
и 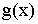 гладкие
в окрестности
гладкие
в окрестности 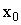 и
и 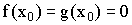
Тогда 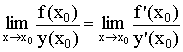
Правило
Лопиталя: Предел
отношения функций равен пределу
отношения их производных.
Доказательство:
Применим
теорему для
и
, 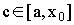 ,
где а
- точка
в окрестности
.
,
где а
- точка
в окрестности
.
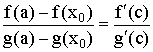 где
где 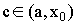 .
.
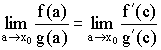
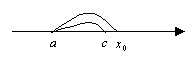
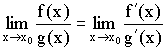
Примеры:
1) 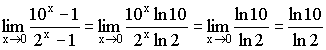
2) 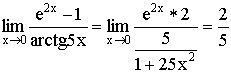
3) 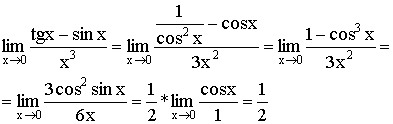
Неопределенности
типа 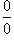
Пусть
заданы две функции f (x) и g (x),
такие, что
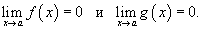
В
этом случае говорят, что функция 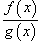 имеет
неопределенность типа
в
точке x
= a.
Чтобы найти предел при x
= a когда
функция
содержит
неопределенность
,
нужно разложить на множители числитель
и/или знаменатель и затем сократить
члены, стремящиеся к нулю.
Примечание:
В данном разделе при вычислении пределов
не используется правило
Лопиталя.
имеет
неопределенность типа
в
точке x
= a.
Чтобы найти предел при x
= a когда
функция
содержит
неопределенность
,
нужно разложить на множители числитель
и/или знаменатель и затем сократить
члены, стремящиеся к нулю.
Примечание:
В данном разделе при вычислении пределов
не используется правило
Лопиталя.
Неопределенности
типа 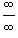
Пусть
две функции f (x) и g (x) обладают
свойством
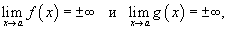
где a является
действительным числом, либо стремится
к + ∞ или − ∞. Говорят, что в этом
случае функция
имеет
в точке a неопределенность
типа
.
Для вычисления предела в этой точке
необходимо разделить числитель и
знаменатель на x в
наивысшей степени.
Неопределенности
типа 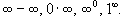
Неопределенности
этих типов сводятся к рассмотренным
выше неопределенностям типа
и
.
12)Вопрос
Формула Тейлора — Пеано Пусть 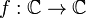 ,
, 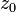 —
предельная точка множества
—
предельная точка множества  и
и 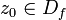 .
Если функция
.
Если функция
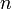 -дифференцируема
в смысле
Ферма — Лагранжа в
точке
,
то справедлива формула Тейлора
— Пеано
-дифференцируема
в смысле
Ферма — Лагранжа в
точке
,
то справедлива формула Тейлора
— Пеано
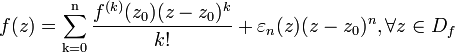
где
εn(z)
- непрерывная в точке z0 функция
и εn(z0)=0.
Применим метод
математической индукции.
Если n=0, то утверждение очевидно при
εn (z)=f(z)-f(z0).
Предположим, что утверждение теоремы справедливо
после замены n на n-1 и что функция f
n-дифференцируема в смысле Ферма-Лагранжа
в точке z0.
Согласно определению, существует такая
n-1 дифференцируемая в смысле Ферма-Лагранжа
в точке z0 функция
φ, что ∀z∈Df,
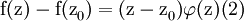
По
предположению
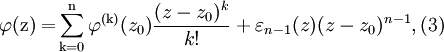
где 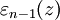 -
непрерывная в точке z0 функция
и
-
непрерывная в точке z0 функция
и 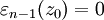 .
Из равенств (2) и (3) получаем:
.
Из равенств (2) и (3) получаем:
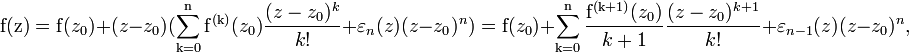
Что
равносильно формуле (1) при 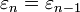
Основные
разложения в ряд Тейлора
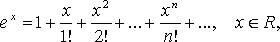
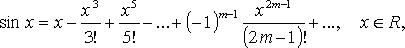
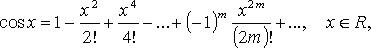
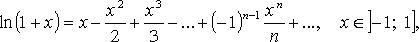
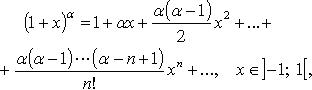
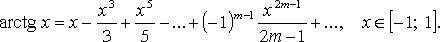
13)Вопрос
Необходимые
и достаточные условия экстремума
функции нескольких
(двух) переменных
Рассмотрим
функцию 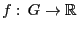 ,
где
,
где 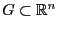 --
открытое множество.
--
открытое множество.
Определение 1. 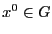 называется
точкой максимума (минимума) функции
называется
точкой максимума (минимума) функции  ,
если
,
если
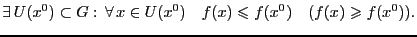
Аналогично
если выполняется строгое неравенство,
точка называется точкой строгого
максимума (строгого минимума).
Теорема 1. (необходимое
условие экстремума) Если 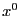 --
точка экстремума и существует
--
точка экстремума и существует 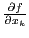 ,
то
,
то 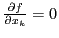 .
.
Доказательство. Частную
производную можно представить как
производную функции одной переменной 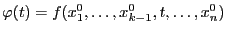 в
точке
в
точке 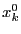 .
Для этой функции точка
также
является точкой экстремума. Тогда, по
необходимому условию экстремума функции
одной переменной
.
Для этой функции точка
также
является точкой экстремума. Тогда, по
необходимому условию экстремума функции
одной переменной 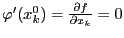 .
. 
Определение 2.
--
стационарная точка функции
,
если
--
дифференцируема в этой точке и 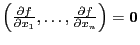 ,
или
--
не дифференцируема в этой точке.
,
или
--
не дифференцируема в этой точке.
Замечание 1. Квадратичная
форма -- многочлен вида 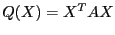 ,
, 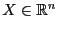 --
положительно определена, если на
положительных переменных она принимает
положительные значения. Для квадратичных
форм существует критерий Сильвестра:
форма положительно определена, если
все главные миноры ее матрицы положительны.
Форма отрицательно определена,
если
--
положительно определена, если на
положительных переменных она принимает
положительные значения. Для квадратичных
форм существует критерий Сильвестра:
форма положительно определена, если
все главные миноры ее матрицы положительны.
Форма отрицательно определена,
если 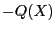 положительно
определена. Тогда главные миноры меняют
знак, начиная с минуса.
положительно
определена. Тогда главные миноры меняют
знак, начиная с минуса.
Теорема 2. (достаточное
условие экстремума) Если
дважды
дифференцируема в стационарной точке
,
то
--
точка минимума (максимума), если
квадратичная форма 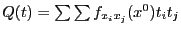 положительно
(отрицательно) определена. Если эта
форма не определена, то экстремума в
этой точке нет. Если она вырождена, то
неизвестно, является ли
точкой
экстремума.
положительно
(отрицательно) определена. Если эта
форма не определена, то экстремума в
этой точке нет. Если она вырождена, то
неизвестно, является ли
точкой
экстремума.
Доказательство. По
формуле Тейлора приращение функции в
точке
можно
записать в виде 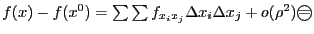 ,
поскольку, по необходимому условию
экстремума, частные производные будут
равны нулю. Перепишем выражение в виде
,
поскольку, по необходимому условию
экстремума, частные производные будут
равны нулю. Перепишем выражение в виде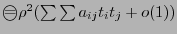 ,
причем
,
причем 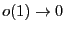 при
при 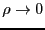 .
Заметим, что новые переменные
.
Заметим, что новые переменные 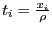 изменяются
на единичной сфере, т.к.
изменяются
на единичной сфере, т.к. 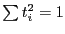 .
Кроме того, квадратичная форма
.
Кроме того, квадратичная форма 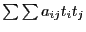 непрерывна
и по теореме Вейерштрасса на сфере
принимает наименьшее значение, обозначим
его
непрерывна
и по теореме Вейерштрасса на сфере
принимает наименьшее значение, обозначим
его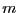 .
Пусть форма положительно определена.
Тогда
.
Пусть форма положительно определена.
Тогда 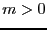 .
Теперь благодаря тому, что
при
можно
подобрать такое
.
Теперь благодаря тому, что
при
можно
подобрать такое 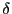 ,
что при
,
что при выполнено
выполнено 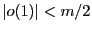 ,
тогда выполнено
,
тогда выполнено  в
этой окрестности. Что и означает,
что
--
точка минимума. Для точки максимума
доказательство аналогично.
в
этой окрестности. Что и означает,
что
--
точка минимума. Для точки максимума
доказательство аналогично.
Замечание 2. В
случае двух переменных матрица
квадратичной формы имеет вид 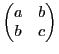 .
Тогда если
.
Тогда если 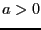 ,
то для положительной определенности
достаточно
,
то для положительной определенности
достаточно 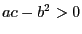 --
тогда имеется минимум. Если же
--
тогда имеется минимум. Если же 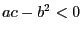 ,
то достигается максимум. Если же
,
то достигается максимум. Если же 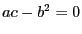 ,
то ничего сказать нельзя.
,
то ничего сказать нельзя.
14)Вопрос Выпуклая функция
Выпуклая
функция — функция,
у которой надграфик является
выпуклым множеством.
Определение
Вещественнозначная
функция, определённая на некотором интервале (в
общем случае на выпуклом
подмножестве некоторого векторного
пространства)
выпукла, если для любых двух значений
аргумента
, 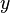 и
для любого числа
и
для любого числа 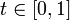 выполняется неравенство
Йенсена:
выполняется неравенство
Йенсена:

Если
это неравенство является строгим для
всех 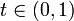 ,
функция называется строго
выпуклой;
если выполняется обратное неравенство,
функция называется вогнутой,
или выпуклой
вверх.
,
функция называется строго
выпуклой;
если выполняется обратное неравенство,
функция называется вогнутой,
или выпуклой
вверх.
NB! Иногда
выпуклая функция определяется как
вогнутая и наоборот.
Свойства
Функция
,
выпуклая на интервале 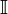 , непрерывна на
всём
, дифференцируема на
всём
за
исключением не более чем счётного
множества точек
и дважды дифференцируема почти везде.
, непрерывна на
всём
, дифференцируема на
всём
за
исключением не более чем счётного
множества точек
и дважды дифференцируема почти везде.
Непрерывная
функция
выпукла
на
тогда
и только тогда, когда для всех
точек 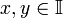 выполняется
неравенство
выполняется
неравенство
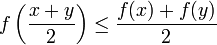
Непрерывно
дифференцируемая функция одной
переменной выпукла на интервале тогда
и только тогда, когда её график лежит
не ниже касательной,
проведённой к этому графику в любой
точке промежутка выпуклости.
Дважды
дифференцируемая функция одной
переменной выпукла на интервале тогда
и только тогда, когда её
вторая производная неотрицательна
на этом интервале. Если вторая производная
дважды дифференцируемой функции строго
положительна, такая функция является
строго выпуклой, однако обратное
неверно (например, функция 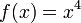 строго
выпукла на
строго
выпукла на 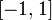 ,
но её вторая производная в точке
,
но её вторая производная в точке 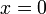 равна
нулю).
равна
нулю).
Если
функции
,
выпуклы,
то любая их линейная
комбинация 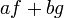 с
положительными коэффициентами
,
с
положительными коэффициентами
, 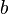 также
выпукла.
также
выпукла.
Локальный
минимум выпуклой
функции является также глобальным
минимумом (соответственно,
для выпуклых вверх функций локальный
максимум является глобальным максимумом).
Любая стационарная
точка выпуклой
функции будет глобальным экстремумом.
Для
выпуклых функций выполняется неравенство
Йенсена:
 где
где 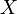 — случайная
величина со
значениями в области
определения функции
,
— случайная
величина со
значениями в области
определения функции
, 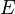 — математическое
ожидание.
— математическое
ожидание.
Точка перегиба функции
Материал
из Википедии — свободной энциклопедииУ
этого термина существуют и другие
значения, см. Точка
перегиба.
Точка
перегиба функции 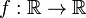 внутренняя
точка
области
определения
,
такая что
непрерывна
в этой точке, существует конечная или
определенного знака бесконечная
производная в этой точке, и
является
одновременно концом интервала строгой
выпуклости вверх и началом интервала
строгой выпуклости вниз, или наоборот.
внутренняя
точка
области
определения
,
такая что
непрерывна
в этой точке, существует конечная или
определенного знака бесконечная
производная в этой точке, и
является
одновременно концом интервала строгой
выпуклости вверх и началом интервала
строгой выпуклости вниз, или наоборот.
Условия
существованияНеобходимое
условие существования точки перегиба: если
функция f(x), дважды дифференцируемая в
некоторой окрестности точки
,
имеет в
точку
перегиба, то 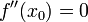 .
.
Достаточное
условие существования точки перегиба: если
функция 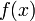 в
некоторой окрестности точки
в
некоторой окрестности точки
 раз
непрерывно дифференцируема,
причем
нечётно
и
раз
непрерывно дифференцируема,
причем
нечётно
и 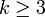 ,
и
,
и 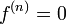 при
при 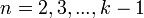 ,
а
,
а 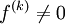 ,
то функция
имеет
в
точку
перегиба.
,
то функция
имеет
в
точку
перегиба.
15)вопросАси́мпто́та[1] (от греч. ασϋμπτωτος —
несовпадающий, не
касающийся) кривой с бесконечной ветвью
— прямая,
обладающая тем свойством, что расстояние
от точки кривой до этой прямой стремится
к нулю при удалении точки вдоль ветви
в бесконечность[2].
Термин впервые появился у Аполлония
Пергского,
хотя асимптоты гиперболы исследовал
ещёАрхимед[3]
Вертикальная
Вертикальная
асимптота — прямая вида 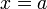 при
условии существования предела
при
условии существования предела  .
.
Как
правило, при определении вертикальной
асимптоты ищут не один предел, а два
односторонних (левый и правый). Это
делается с целью определить, как функция
ведёт себя по мере приближения к
вертикальной асимптоте с разных сторон.
Например:
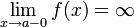
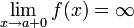
Замечание:
обратите внимание на знаки бесконечностей
в этих равенствах.
]Горизонтальная
Горизонтальная
асимптота — прямая вида 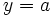 при
условии существования предела
при
условии существования предела
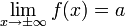 .
.
Наклонная
асимптота — прямая вида 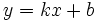 при
условии существования пределов
при
условии существования пределов
Пример
наклонной асимптоты
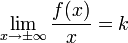
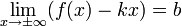
Замечание:
функция может иметь не более двух
наклонных(горизонтальных) асимптот!
Замечание:
Если хотя бы один из двух упомянутых
выше пределов не существует (или
равен 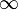 ),
то наклонной асимптоты при
),
то наклонной асимптоты при 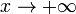 (или
(или 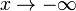 )
не существует!
)
не существует!
Связь
между наклонной и горизонтальной
асимптотами
Если
при вычислении предела 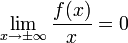 ,
то очевидно, что наклонная асимптота
совпадает с горизонтальной. Какова же
связь между этими двумя видами асимптот?
,
то очевидно, что наклонная асимптота
совпадает с горизонтальной. Какова же
связь между этими двумя видами асимптот?
Дело
в том, что
горизонтальная асимптота является
частным случаем наклонной при
,
и из выше указанных замечаний следует,
что
Функция
имеет или только одну наклонную
асимптоту, или одну вертикальную
асимптоту, или одну наклонную и одну
вертикальною, или две наклонных, или
две вертикальных, либо же вовсе не
имеет асимптот.
Существование
указанных в п. 1.) асимптот напрямую
связано с существованием соответствующих
пределов.
Порядок нахождения асимптот
Нахождение
вертикальных асимптот.
Нахождение
двух пределов
Нахождение
двух пределов
:
если 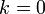 в
п. 2.), то
в
п. 2.), то 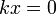 ,
и предел
ищется
по формуле горизонтальной асимптоты,
.
,
и предел
ищется
по формуле горизонтальной асимптоты,
.
Наклонная асимптота — выделение целой части
Также
наклонную асимптоту можно найти, выделив
целую часть. Например:
Дана функция 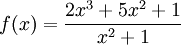 .
.
Разделив
нацело числитель на знаменатель,
получим:
 .
.
При
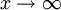 ,
,
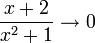 ,
то есть:
,
то есть:
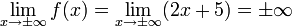 ,
,
и 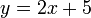 является
искомым уравнением асимптоты.
является
искомым уравнением асимптоты.
16)Вопрос
Первообразная
и неопределенный интеграл
Первообразной
функцией для функции f(x) называется
такая функция F(х), производная которой
равна данной функции
F'(x)
= f(x).
Обозначение
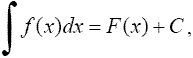
где
F'(x) = f(x). Функция f(x) называется
подынтегральной функцией, а выражение
f(x)dx - подынтегральным выражением.
П.2.
Свойства неопределенного интеграла
1°.
Производная неопределенного интеграла
равна подынтегральной функции;
дифференциал от неопределенного
интеграла равен подынтегральному
выражению, т.е.
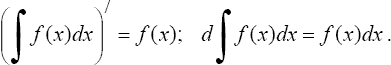
2°.
Неопределенный интеграл от дифференциала
некоторой функции равен сумме этой
функции и произвольной постоянной,
т.е.
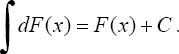
3°.
Постоянный множитель можно вынести из
под знака интеграла, т.е. если k = const ≠
0, то
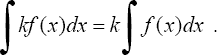
4°
. Неопределенный интеграл от алгебраической
суммы двух функций равен алгебраической
сумме интегралов от этих функций в
отдельности.
17)Вопрос
Замена переменной в определенном
интеграле
Теги: интеграл, функция, определенный
интеграл, лекция
по высшей математики, формула, высшая
математика
|
При
вычислении определенных интегралов
с использованием формулы Ньютона-Лейбница
предпочтительно жестко не разграничивать
этапы решения задачи (нахождение
первообразной подынтегральной
функции, нахождение приращения
первообразной). Такой подход,
использующий, в частности, формулы
замены переменной и интегрирования
по частям для определенного интеграла,
обычно позволяет упростить запись
решения.
ТЕОРЕМА.
Пусть функция φ(t) имеет непрерывную
производную на отрезке [α,β], а=φ(α),
в=φ(β) и функция f(х) непрерывна в каждой
точке х вида х=φ(t), где t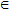 [α,β].
[α,β].
Тогда
справедливо следующее равенство:

Эта
формула носит название формулы замены
переменной в определенном интеграле.
Подобно
тому, как это было в случае неопределенного
интеграла, использование замены
переменной позволяет упростить
интеграл, приблизив его к табличному
(табличным). При этом в отличие от
неопределенного интеграла в данном
случае нет необходимости возвращаться
к исходной переменной интегрирования.
Достаточно лишь найти пределы
интегрирования α и β по новой переменной
t как решение относительно переменной
t уравнений φ(t)=а и φ(t)=в. На практике,
выполняя замену переменной, часто
начинают с того, что указывают выражение
t=ψ(х) новой переменной через старую.
В этом случае нахождение пределов
интегрирования по переменной t
упрощается: α=ψ(а), β=ψ(в).
Пример
19. Вычислить 
Положим
t=2-х2.
Тогда dt=d(2-х2)=(2-х2)'dx=-2xdx
и xdx=-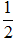 dt.
Если х=0, то t=2-02=2,
и если х=1, то t=2-12=1.
Следовательно:
dt.
Если х=0, то t=2-02=2,
и если х=1, то t=2-12=1.
Следовательно:
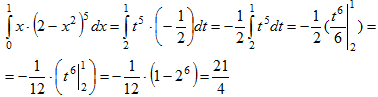
Пример
20. Вычислить 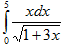
Воспользуемся
заменой переменной 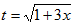 .
Тогда
.
Тогда 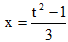 и
и 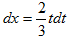 .
Если х=0, то t=1 и, если х=5, то t=4. Выполняя
замену, получим:
.
Если х=0, то t=1 и, если х=5, то t=4. Выполняя
замену, получим:
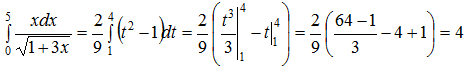
Пример
21. Вычислить 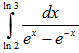
Положим
t=ex.
Тогда x=lnt, dx=dt/t и, если x=ln2, то t=2, если
х=ln3, то t=3. Выполняя замену, получаем:
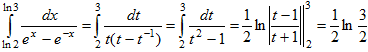
|
Интегрирование
по частям
|
|
Пусть u(x) и v(x) являются
дифференцируемыми функциями.
Дифференциал произведения
функций u и vопределяется
формулой
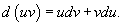
Проинтегрировав
обе части этого выражения, получим
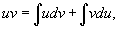
или,
переставляя члены,
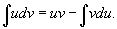
Это
и есть формула
интегрирования по частям.
|
Пример
1
|
|
Вычислить
интеграл 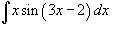 .
.
Решение.
Используем
формулу интегрирования по частям 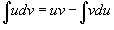 .
Пусть
.
Пусть 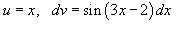 .
Тогда
.
Тогда
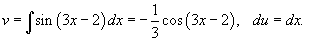
Следовательно,
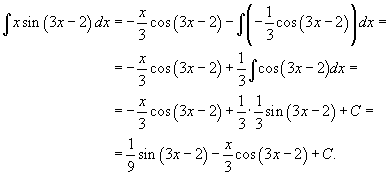
|
18)вопросФункция
называется рациональной,
если ее можно представить в виде
отношения двух многочленов. Например,
если R(x)
— рациональная функция одной переменной x,
то
|
R(x)
=
am xm + am −
1 xm −
1 +
… + a1 x + a0
|
bn xn + bn −
1 xn −
1 +
… + b1 x + b0
|
≡
.
|
|
Здесь,
как обычно, индексы у Pm(x)
и Qn(x)
указывают степени этих многочленов
.
Многочлены
являются рациональными функциями (у
них знаменатели тождественно равны
единице). Если рациональная функция не
является многочленом, то она называется
дробной .
Рациональная
функция называется правильной, если
степень многочлена в числителе меньше
степени многочлена в знаменателе и
неправильной, если степень многочлена
в числителе больше либо равна степени
многочлена в знаменателе .
Неправильная рациональная функция
представима в виде
где Lm − n —
многочлен степени (m − n)
, называемый целой
частью рациональной
функции. Он находится путем деления
многочлена Pm на Qn .
Многочлен Us —
остаток при этом делении.
При
интегрировании рациональных функций
используется следующая теорема о
разложении рациональной функции:
Теорема Правильную
рациональную функцию одной
переменной x можно единственным
образом представить в виде суммы
элементарных дробей
где A , M , N , a , p , q —
действительные числа и k —
натуральные числа.
В
этой сумме каждому действительному
нулю a кратности k знаменателя Qn(x)
соответствуют k слагаемых
Каждой
паре комплексно сопряженных нулей
кратности k знаменателя Qn(x)
(являющихся нулями квадратного
трехчлена x2 +
2px + q )
соответствуют k слагаемых
Представление
правильной рациональной функции в виде
суммы элементарных дробей называется
разложением на элементарные дроби.
Коэффициенты
элементарных дробей, фигурирующих в
разложении, однозначно определяются
условием тождественности правильной
рациональной функции и ее разложения.
Алгоритм
интегрирования рациональной функции R(x)
Выделяем
целую часть, если функция R(x)
неправильная.
Находим
нули знаменателя функции R(x).
Разлагаем
знаменатель функции R(x)
на линейные множители, соответствующие
действительным нулям и квадратные
трехчлены, соответствующие парам
комплексно сопряженных нулей знаменателя.
Разлагаем
правильную часть функции R(x)
на сумму элементарных дробей.
Интегрируем
целую часть (если она есть) и элементарные
дроби.
Складываем
полученные интегралы.
19)вопросВ математическом
анализе дифференциальным
биномом или биномиальным
дифференциалом называется интеграл вида
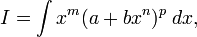
где m, n, p, a, b — действительные
числа.
Свойства Выразимость в элементарных функциях
Дифференциальный
бином выражается в элементарных
функциях только
в трёх случаях:
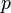 —
целое
число;
—
целое
число;
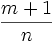 —
целое
число;
—
целое
число;
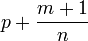 —
целое
число.
—
целое
число.
Связь с бета-функцией и гипергеометрической функцией
Дифференциальный
бином выражается через неполную
бета-функцию:
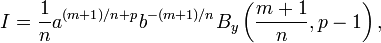
где  ,
а также через гипергеометрическую
функцию:
,
а также через гипергеометрическую
функцию:
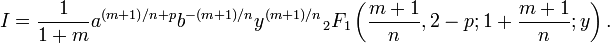
20)Вопрос
Пусть R(x,xr1,xr2,...,xrn) – рациональная
функция от x,xr1,xr2,...,xrn. Эта
функция, а следовательно, и интеграл
от неё, рационализируется
подстановкой x=tr, гдеr – наименьшее
общее кратное чисел r1,r2,...,rn.
Тогда dx=rtr−1dt и
под интегралом стоит рациональная
функция от t. Аналогично,
если подынтегральное
выражениеR(x,ax+bcx+dr1,ax+bcx+dr2,...,ax+bcx+drn) есть
рациональная функция
отx,ax+bcx+dr1,ax+bcx+dr2,...,ax+bcx+drn, то подынтегральная
функция рационализируется
подстановкой ax+bcx+d=tr, где r – наименьшее
общее кратное чисел r1,r2,...,rn.
Тогда x=dtr−b−ctr+a. Подставляя
в исходное выражение, получаем
рациональную функцию от t.
Примеры.
1.
Вычислить ∫xx−x23 dx. Наименьшее
общее кратное чисел 2 и 3 равно 6. Поэтому
делаем замену x=t6. Тогда dx=6t5dt и
∫xx−x23 dx=∫t36t5dtt6−t4=6∫t4t2−1dt=6∫t4−1+1t2−1dt=6∫(t2+1)dt+6∫dtt2−1=6∫(t2+1)dt+3∫dtt−1−3∫dtt+1= =2t3+6t+3ln|t−1|−3ln|t+1|+C=2t3+6t+3ln|t−1t+1|+C=2x+6 x6+3ln|x6−1x6+1|+C.
2.
Вычислить ∫(x+2)35x+2−(x+2)85 dx.
Наименьшее общее кратное чисел 2 и 5
равно 10. Поэтому делаем
замену x+2=t10. Тогда dx=10t9dt и
∫(x+2)35x+2−(x+2)85 dx=∫t610t9dtt5−t16=10∫t101−t11dt=−1011ln| 1−t11 |+C=−1

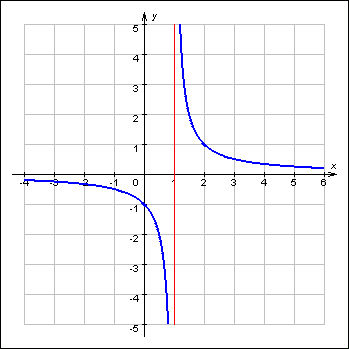
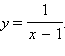 Она
разрывна в точке x0 = 1,
так как не существует в этой точке.
Она
разрывна в точке x0 = 1,
так как не существует в этой точке.![]() непрерывна
в ней при условии, чтоg (x0) ≠ 0.
непрерывна
в ней при условии, чтоg (x0) ≠ 0.![]() еорема
Вейерштрасса. Если
функция f (x) непрерывна
на отрезке [a; b],
то она ограничена на этом отрезке и
достигает своего наибольшего и
наименьшего значения.
еорема
Вейерштрасса. Если
функция f (x) непрерывна
на отрезке [a; b],
то она ограничена на этом отрезке и
достигает своего наибольшего и
наименьшего значения.
![]() (и
возможно, не одна) такая, что f (x) = y.
(и
возможно, не одна) такая, что f (x) = y. Пусть функция
Пусть функция ![]() определена
в некоторой окрестности точки
определена
в некоторой окрестности точки ![]() ,
и дифференцируема в
ней:
,
и дифференцируема в
ней: ![]() .
Касательной прямой к графику функции
в
точке
.
Касательной прямой к графику функции
в
точке ![]() называется
график линейной
функции,
задаваемой уравнением
называется
график линейной
функции,
задаваемой уравнением![]() .
.![]() то
касательной прямой в этой точке
называется вертикальная прямая,
задаваемая уравнением
то
касательной прямой в этой точке
называется вертикальная прямая,
задаваемая уравнением![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
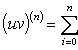
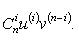
![]()
![]() n-кратно
дифференцируемы, то
n-кратно
дифференцируемы, то ![]()
![]()
![]()
![]()
![]() .
.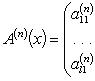
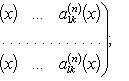
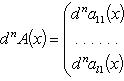
![]() или
или ![]() в
т.
в
т.![]() ■
■![]() (рис.
10.1), тогда
(рис.
10.1), тогда![]() при
при![]() и
и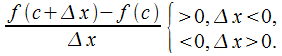
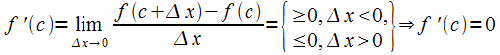 ◙
◙![]() в
точке с абсциссой
в
точке с абсциссой![]() параллельна
оси
параллельна
оси![]() .
.![]() .
Тогда
.
Тогда![]() ■
■![]() следует
по свойству 10 непрерывных
на
следует
по свойству 10 непрерывных
на![]() функций,
что
функций,
что![]() .
.![]() ;
;![]() в
силу
в
силу![]() .
.![]() ,
тогда согласно теореме Ферма
,
тогда согласно теореме Ферма![]() .
.![]() .
Тогда
.
Тогда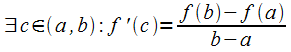 ■
■![]() ,
для которой верны условия теоремы
Ролля:
,
для которой верны условия теоремы
Ролля:![]() или
или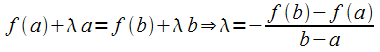 .
.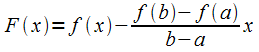 .
.![]() :
: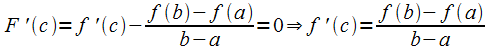 ◙
◙![]() .
Угловой коэффициент касательной в
т.
.
Угловой коэффициент касательной в
т. ![]() .
Следовательно, на графике функции
.
Следовательно, на графике функции![]() .
.![]() .
Тогда
.
Тогда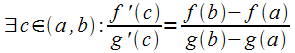 ■
■![]() .
В противном случае согласно теореме
Ролля
.
В противном случае согласно теореме
Ролля![]() .
.![]() .
Подберём такое
.
Подберём такое![]() ,
чтобы
,
чтобы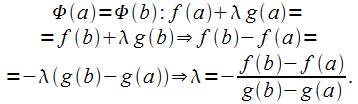
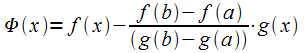 .
По теореме Ролля
.
По теореме Ролля 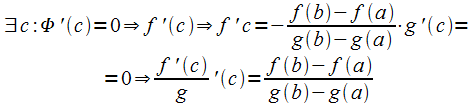 .
.![]() .
.![]() и
и ![]() гладкие
в окрестности
гладкие
в окрестности ![]() и
и ![]()
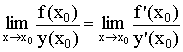
![]() ,
где а
- точка
в окрестности
.
,
где а
- точка
в окрестности
.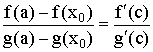 где
где ![]() .
.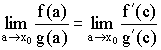
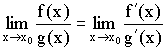
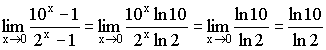
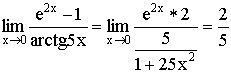
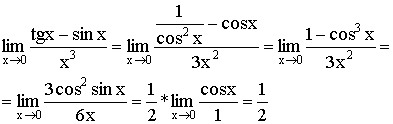
![]()
![]()
![]() имеет
неопределенность типа
в
точке x
= a.
Чтобы найти предел при x
= a когда
функция
содержит
неопределенность
,
нужно разложить на множители числитель
и/или знаменатель и затем сократить
члены, стремящиеся к нулю.
Примечание:
В данном разделе при вычислении пределов
не используется правило
Лопиталя.
имеет
неопределенность типа
в
точке x
= a.
Чтобы найти предел при x
= a когда
функция
содержит
неопределенность
,
нужно разложить на множители числитель
и/или знаменатель и затем сократить
члены, стремящиеся к нулю.
Примечание:
В данном разделе при вычислении пределов
не используется правило
Лопиталя.
![]()
![]()
![]()
![]() ,
, ![]() —
предельная точка множества
—
предельная точка множества ![]() и
и ![]() .
Если функция
.
Если функция
![]() -дифференцируема
в смысле
Ферма — Лагранжа в
точке
,
то справедлива формула Тейлора
— Пеано
-дифференцируема
в смысле
Ферма — Лагранжа в
точке
,
то справедлива формула Тейлора
— Пеано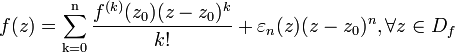
![]()
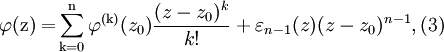
![]() -
непрерывная в точке z0 функция
и
-
непрерывная в точке z0 функция
и ![]() .
Из равенств (2) и (3) получаем:
.
Из равенств (2) и (3) получаем: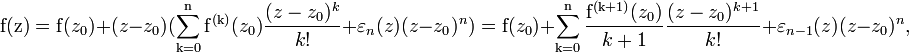
![]()
![]()
![]()
![]()
![]()
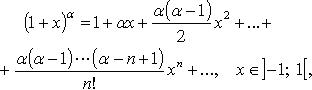
![]()
![]() ,
где
,
где ![]() --
открытое множество.
--
открытое множество.![]() называется
точкой максимума (минимума) функции
называется
точкой максимума (минимума) функции ![]() ,
если
,
если![]()
![]() --
точка экстремума и существует
--
точка экстремума и существует ![]() ,
то
,
то ![]() .
.![]() в
точке
в
точке ![]() .
Для этой функции точка
также
является точкой экстремума. Тогда, по
необходимому условию экстремума функции
одной переменной
.
Для этой функции точка
также
является точкой экстремума. Тогда, по
необходимому условию экстремума функции
одной переменной ![]() .
. ![]()
![]() ,
или
--
не дифференцируема в этой точке.
,
или
--
не дифференцируема в этой точке.![]() ,
, ![]() --
положительно определена, если на
положительных переменных она принимает
положительные значения. Для квадратичных
форм существует критерий Сильвестра:
форма положительно определена, если
все главные миноры ее матрицы положительны.
Форма отрицательно определена,
если
--
положительно определена, если на
положительных переменных она принимает
положительные значения. Для квадратичных
форм существует критерий Сильвестра:
форма положительно определена, если
все главные миноры ее матрицы положительны.
Форма отрицательно определена,
если ![]() положительно
определена. Тогда главные миноры меняют
знак, начиная с минуса.
положительно
определена. Тогда главные миноры меняют
знак, начиная с минуса.![]() положительно
(отрицательно) определена. Если эта
форма не определена, то экстремума в
этой точке нет. Если она вырождена, то
неизвестно, является ли
точкой
экстремума.
положительно
(отрицательно) определена. Если эта
форма не определена, то экстремума в
этой точке нет. Если она вырождена, то
неизвестно, является ли
точкой
экстремума.![]() ,
поскольку, по необходимому условию
экстремума, частные производные будут
равны нулю. Перепишем выражение в виде
,
поскольку, по необходимому условию
экстремума, частные производные будут
равны нулю. Перепишем выражение в виде![]() ,
причем
,
причем ![]() при
при ![]() .
Заметим, что новые переменные
.
Заметим, что новые переменные ![]() изменяются
на единичной сфере, т.к.
изменяются
на единичной сфере, т.к. ![]() .
Кроме того, квадратичная форма
.
Кроме того, квадратичная форма ![]() непрерывна
и по теореме Вейерштрасса на сфере
принимает наименьшее значение, обозначим
его
непрерывна
и по теореме Вейерштрасса на сфере
принимает наименьшее значение, обозначим
его![]() .
Пусть форма положительно определена.
Тогда
.
Пусть форма положительно определена.
Тогда ![]() .
Теперь благодаря тому, что
при
можно
подобрать такое
.
Теперь благодаря тому, что
при
можно
подобрать такое ![]() ,
что при
,
что при![]() выполнено
выполнено ![]() ,
тогда выполнено
,
тогда выполнено ![]() в
этой окрестности. Что и означает,
что
--
точка минимума. Для точки максимума
доказательство аналогично.
в
этой окрестности. Что и означает,
что
--
точка минимума. Для точки максимума
доказательство аналогично.
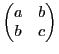 .
Тогда если
.
Тогда если ![]() ,
то для положительной определенности
достаточно
,
то для положительной определенности
достаточно ![]() --
тогда имеется минимум. Если же
--
тогда имеется минимум. Если же ![]() ,
то достигается максимум. Если же
,
то достигается максимум. Если же ![]() ,
то ничего сказать нельзя.
,
то ничего сказать нельзя.![]() и
для любого числа
и
для любого числа ![]() выполняется неравенство
Йенсена:
выполняется неравенство
Йенсена:![]()
![]() ,
функция называется строго
выпуклой;
если выполняется обратное неравенство,
функция называется вогнутой,
или выпуклой
вверх.
,
функция называется строго
выпуклой;
если выполняется обратное неравенство,
функция называется вогнутой,
или выпуклой
вверх.![]() , непрерывна на
всём
, дифференцируема на
всём
за
исключением не более чем счётного
множества точек
и дважды дифференцируема почти везде.
, непрерывна на
всём
, дифференцируема на
всём
за
исключением не более чем счётного
множества точек
и дважды дифференцируема почти везде.![]() выполняется
неравенство
выполняется
неравенство![]()
![]() строго
выпукла на
строго
выпукла на ![]() ,
но её вторая производная в точке
,
но её вторая производная в точке ![]() равна
нулю).
равна
нулю).![]() с
положительными коэффициентами
,
с
положительными коэффициентами
, ![]() также
выпукла.
также
выпукла.![]() где
где ![]() — случайная
величина со
значениями в области
определения функции
,
— случайная
величина со
значениями в области
определения функции
, ![]() — математическое
ожидание.
— математическое
ожидание.![]() внутренняя
точка
области
определения
,
такая что
непрерывна
в этой точке, существует конечная или
определенного знака бесконечная
производная в этой точке, и
является
одновременно концом интервала строгой
выпуклости вверх и началом интервала
строгой выпуклости вниз, или наоборот.
внутренняя
точка
области
определения
,
такая что
непрерывна
в этой точке, существует конечная или
определенного знака бесконечная
производная в этой точке, и
является
одновременно концом интервала строгой
выпуклости вверх и началом интервала
строгой выпуклости вниз, или наоборот.![]() .
.![]() в
некоторой окрестности точки
в
некоторой окрестности точки
![]() раз
непрерывно дифференцируема,
причем
нечётно
и
раз
непрерывно дифференцируема,
причем
нечётно
и ![]() ,
и
,
и ![]() при
при ![]() ,
а
,
а ![]() ,
то функция
имеет
в
точку
перегиба.
,
то функция
имеет
в
точку
перегиба.![]() при
условии существования предела
при
условии существования предела ![]() .
.![]()
![]()
![]() при
условии существования предела
при
условии существования предела![]() .
.![]() при
условии существования пределов
при
условии существования пределов![]()
![]()
![]() ),
то наклонной асимптоты при
),
то наклонной асимптоты при ![]() (или
(или ![]() )
не существует!
)
не существует!![]() ,
то очевидно, что наклонная асимптота
совпадает с горизонтальной. Какова же
связь между этими двумя видами асимптот?
,
то очевидно, что наклонная асимптота
совпадает с горизонтальной. Какова же
связь между этими двумя видами асимптот?![]() в
п. 2.), то
в
п. 2.), то ![]() ,
и предел
ищется
по формуле горизонтальной асимптоты,
.
,
и предел
ищется
по формуле горизонтальной асимптоты,
.![]() .
.![]() .
.![]() ,
,
![]() ,
то есть:
,
то есть:![]() ,
,![]() является
искомым уравнением асимптоты.
является
искомым уравнением асимптоты.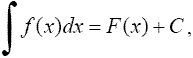
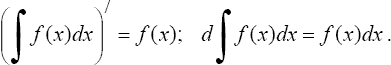
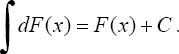
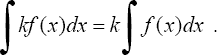
![]() [α,β].
[α,β].

![]() dt.
Если х=0, то t=2-02=2,
и если х=1, то t=2-12=1.
Следовательно:
dt.
Если х=0, то t=2-02=2,
и если х=1, то t=2-12=1.
Следовательно: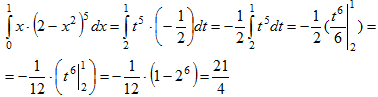
![]()
![]() .
Тогда
.
Тогда ![]() и
и ![]() .
Если х=0, то t=1 и, если х=5, то t=4. Выполняя
замену, получим:
.
Если х=0, то t=1 и, если х=5, то t=4. Выполняя
замену, получим: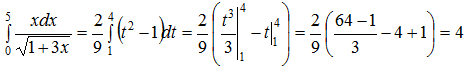
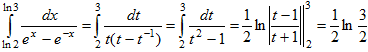
![]()
![]()
![]()
![]() .
.![]() .
Пусть
.
Пусть ![]() .
Тогда
.
Тогда![]()
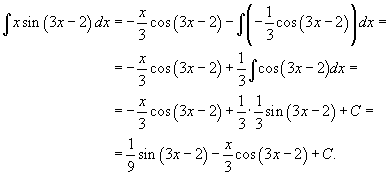
![]()
![]() —
целое
число;
—
целое
число;![]() —
целое
число;
—
целое
число;![]() —
целое
число.
—
целое
число.![]()
![]() ,
а также через гипергеометрическую
функцию:
,
а также через гипергеометрическую
функцию:![]()
