7)Вопрос

 Дифференциалом функции   (обозначается через   ) называется следующее выражение:

где dx -- дифференциал x при условии, что функция имеет производную.

Предположим, что существует следующее равенство функций:

тогда дифференциал от равенства есть

Для решения дифференциальных уравнений используют много разных способов: метод разделения переменных, метод вариации и т.д.

Например, в методе разделения переменных используется определение дифференциала функции т.е.

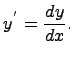
Также это определение используется во многих других методах. 

Дифференци́руемая (в точке) фу́нкция — это функция, у которой существует дифференциал (в данной точке). Дифференцируемая на некотором множестве функция — это функция, дифференцируемая в каждой точке данного множества. Дифференцируемость является одним из фундаментальных понятий в математике и имеет значительное число приложений как в самой математике, так и в других естественных науках.

Приращение дифференцируемой в данной точке функции можно представить как линейную функцию приращения аргумента с точностью до величин более высокого порядка малости. Это означает, что для достаточно малых окрестностей данной точки функцию можно заменить линейной (скорость изменения функции можно считать неизменной). Линейная часть приращения функции называется ее дифференциалом (в данной точке).

Необходимым, но не достаточным условием дифференцируемости является непрерывность функции. В случае функции от одной вещественной переменной дифференцируемость равносильна существованию производной. В случае функции нескольких вещественных переменных необходимым (но не достаточным) условием дифференцируемости является существование частных производных по всем переменным. Для дифференцируемости функции нескольких переменных в точке достаточно, чтобы частные производные существовали в некоторой окрестности рассматриваемой точки и были непрерывны в данной точке.^[1]

В случае функции комплексной переменной дифференцируемость в точке часто называется моногенностью и существенно отличается от понятия дифференцируемости в вещественном случае. Ключевую роль в этом играет так называемое условие Коши — Римана. Функция, моногенная в окрестности точки, называется голоморфной в этой точке.^[2][3]

В функциональном анализе существует обобщение понятия дифференцирования на случай отображений бесконечномерных пространств — производные Гато и Фреше.

Непрерывность функций

Функция f (x), определенная в некоторой окрестности точки a, называется непрерывной в этой точке, если 

Пусть функция определена в некоторой окрестности точки a, быть может, за исключением самой точки a. Точка a называется точкой разрыва, если эта функция либо не определена в точке a, либо определена, но не является непрерывной в точке a.

Чаще всего разрыв возникает по двум причинам:

1. функция задана различными выражениями на разных участках, и в граничных точках эти выражения имеют различные пределы;

2. функция не определена в данной точке.