Показатели сравнительной экономической эффективности

Показатели расчетов	Значение
Затраты на создание системы, руб.
Текущие затраты на содержание и эксплуатацию ИС (выполнение процесса) по базовому варианту, руб.
Текущие затраты на содержание и эксплуатацию ИС (выполнение процесса) по внедряемому варианту
Ожидаемая условно-годовая экономия, руб.
Ожидаемый годовой экономический эффект, руб.
Расчетный коэффициент экономической эффективности капитальных вложений
Расчетный срок окупаемости капитальных вложений, год

Таблица 6.7

Динамические показатели эффективности капитальных вложений

Показатели расчетов	Значение
Затраты на создание системы, руб.
Текущие затраты на содержание и эксплуатацию ЭИС, руб.
Чистый дисконтированный доход, руб.
Индекс доходности
Дисконтированный срок окупаемости, год
Внутренняя норма доходности

Контрольные вопросы

1. Какие факторы обуславливают повышение эффективности организации и управления транспортного процесса при внедрении ИС?

2. Какие затраты включают затраты на создание ИС?

3. Какие затраты включают в расчет текущих затрат на выполнение процесса?

4. Назовите показатели экономической эффективности.

5. Что показывает сравнительная экономическая эффективность?

6. Что показывают динамические показатели эффективности капитальных вложений?

7. Оптимизационная модель перевозки грузов на основе программы «Поиск решения»

Цель практической работы

Овладение практическими навыками по разработке оптимизационной модели перевозки грузов с помощью программы «Поиск решения».

Теоретические аспекты работы

Программный инструментарий оптимизатора Поиск решения является надстройкой Microsoft Excel. В меню Сервис оптимизатор обозначен как Поиск решения.

Перед применением программы Поиск решения Microsoft Excel, необходимо осуществить постановку задачи, т.е. построить математическую модель: определить целевую функцию, основные ограничения и граничные условия. На языке MS Excel соответственно – целевую и изменяемые ячейки и ограничения, которые будут учитываться в процессе анализа.

Целевой ячейкой называется ячейка модели рабочего листа, значение которой следует оптимизировать (максимизировать, минимизировать, приравнять желаемому числовому значению). Обычно эта ячейка содержит введенную пользователем формулу, которая ссылается на изменяемые ячейки.

Изменяемые ячейки – это ячейки, значения которых автоматически изменяются программой оптимизатора для поиска оптимального решения. Их использует целевая ячейка формулы-решения. Для того чтобы влиять на решение, переменные должны быть связаны (прямо или косвенно) с решением и ограничениями. Программа Поиск решения изменяет значение этих ячеек до тех пор, пока не будет найдено решение.

Ограничением называется значение ячейки, которое должно находиться в определенных пределах или удовлетворять целевым значениям. Ограничения могут быть наложены на целевую или изменяемые ячейки.

Работа программы начинается с открытия нужного рабочего листа, выбора в меню Сервис команды Поиск решения (рис. 7.1.).

Рис.7.1. Вид диалогового окна «Поиск решения»

В окно Установить целевую ячейку вводится имя или ссылка на ячейку, для которой нужно найти экстремальное значение (минимум, максимум). Целевая ячейка должна содержать формулу.

В окно Изменяя ячейки вводятся имена или ссылки на ячейки, значения которых будут изменяться до тех пор, пока не будут выполнены все ограничения задачи и получено требуемое значение в целевой ячейке.

В окно Ограничения данные вводятся путем использования кнопок Добавить…, Изменить… и Удалить (рис.7.1.). При обращении к первым двум кнопкам возникают соответствующие диалоговые подокна. Ограничения в виде верхних (<=) и нижних (>=) пределов или равенства (=) могут задаваться для любой ячейки, включая целевую. С помощью оператора целое можно ввести ограничение целочисленности (цел) для изменяемых ячеек. Имеется возможность указать до 500 ограничений – по 2 для каждой изменяемой ячейки плюс 100 дополнительных ограничений.

Процедура решения запускается кнопкой Выполнить. Время решения зависит от числа изменяемых ячеек, размера и сложности рабочего листа, сложности задачи. Сама процедура представляет собой выполнение ряда последовательных итераций. На каждой итерации пересчитываются значения рабочего листа по новому набору изменяемых ячеек, при этом проверяются ограничения и оптимальные значения ячеек. Выполнение процедуры завершается при нахождении решения с приемлемой точностью, либо при невозможности успешного продолжения решения, либо при выполнении максимального числа итераций или исчерпании предельно допустимого времени решения.

На заключительном этапе программа дает сообщение об отыскании оптимального решения или о невозможности его получения в диалоговом окне Результаты поиска решения (рис.2).

Р ис. 7.2. Вид диалогового окна «Результаты поиска решения»

Пример «Задача перевозки грузов»

В файле «Модель_ Транспортная задача» представлена задача доставки товаров с трех заводов на пять региональных складов. Товары могут доставляться с любого завода на любой склад, однако, очевидно, что стоимость доставки на большее расстояние будет большей. Требуется определить количество перевозок между каждым заводом и складом, в соответствии с потребностями складов и производственными возможностями заводов, при которых затраты на перевозку минимальны. Исходные данные и расчетные формулы приведены на рабочем листе файла «Модель_Транспортная задача». Вид этого рабочего листа представлен на рис. 7.3.

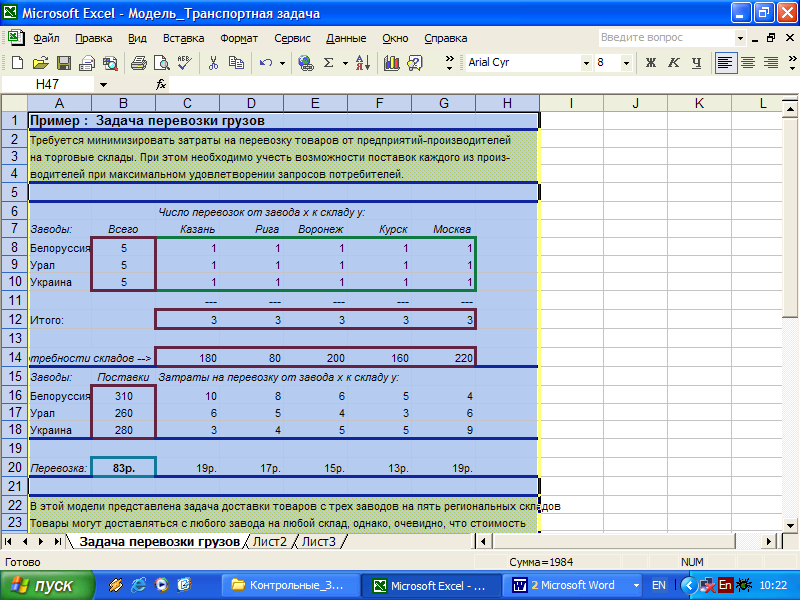
Рис. 7.3. Рабочий лист «Задача перевозки грузов»: исходные данные

Решение

Математическая модель транспортной задачи записывается следующим образом:

минимизировать целевую функцию

при ограничениях , ,

где – затраты на перевозки единицы товара от i-го завода к j-му складу; – объемы перевозок от i-го завода к j-му складу; – производственная возможность завода I; – потребность склада j.

Размещение условия задачи на рабочем листе (целевой функции, переменных и ограничений) представлено в табл.1.

Таблица 7.1

Целевая функция	B20	Цель – уменьшение всех транспортных расходов
Изменяемые ячейки	C8:G10	Объемы перевозок от каждого из заводов к каждому складу
Ограничения	B8:B10<=B16:B18	Количество перевезенных грузов не может превышать производственных возможностей заводов
Ограничения	C12:G12>=C14:G14	Количество доставляемых грузов не должно быть меньше потребностей складов
	C8:G10>=0	Число перевозок не может быть отрицательным
Затраты на перевозку ед. товара	С16:G18	Стоимость перевозок от каждого завода к каждому складу

Последовательность действий решения задачи:

1. В окне «Поиск решения» установите целевую ячейку, равную минимальному значению (В20);

2. Установите изменяемые ячейки (C8:G10);

3. Добавьте ограничения (В8:В10<=В16:В18; C12:G12>=C14:G14; C8:G10>=0);

4. Нажав «Выполнить», найдите решение задачи.

Решенная задача представлена на рис. 7.4.

Рис.7.4. Рабочий лист «Задача перевозки грузов»: решение

Выводы по решению задачи

Наиболее оптимальным является осуществление перевозок из завода на Украине на склады: в Казани в количестве 180, в Риге – 80, в Воронеже – 20; из завода на Урале на склады: в Воронеже в количестве 180, в Курске – 80; из завода в Белоруссии на склады: в Курске в количестве 80, в Москве – 220. При этом удовлетворяются потребности складов: в Казани потребность 180 ездок – доставка 180; в Риге 80=80; в Воронеже 200=200; Курске 160=160; Москве 220=220 и возможности заводов в Белоруссии 300<=310, на Урале 260<=260, на Украине 280<=280. Затраты на перевозки при таком решении минимальны, составляют 3200 у.е.

Задача для решения

Имеются три поставщика и четыре потребителя. Мощность поставщиков и спросы потребителей, а также затраты на перевозку единицы груза для каждой пары «поставщик - потребитель» сведены в табл. 2.

Спрос первого потребителя на товар первого поставщика (Х) проставляется в виде числа равного номеру студента в списке группы.

Таблица 7.2

Поставщики	Мощность поставщиков	Потребители и их спрос
		1	2	3	4
		Х	110	40	110
1	60	1	2	5	3
2	120	1	6	5	2
3	100	6	3	7	4

Найти объемы перевозок для каждой пары «поставщик - потребитель» так, чтобы:

• мощности всех поставщиков были реализованы;

• спросы всех потребителей были удовлетворены;

• суммарные затраты на перевозку были минимальны.

Последовательность действий решения задачи:

1. Сформируйте рабочий лист с условием задачи (табл 7.2) в программе Microsoft Excel.

2. В окне «Поиск решения» установите целевую ячейку, равную минимальному значению.

3. Установите изменяемые ячейки.

4. Добавьте ограничения.

5. В подпункте «Параметры» установите требуемые условием задачи значения.

6. Нажав «Выполнить», найдите решение задачи.

Контрольные вопросы

1. В чем суть оптимизационной модели перевозки грузов?

2. Как представляется математическая модель перевозки грузов в ПП «Поиск решения»?

3. На языке MS Excel какие ячейки называются целевой и изменяемыми ячейки?