Ірраціональні рівняння
1. Рівняння на ОДЗ.
2. Зведення рівняння в квадрат.
3. Метод замін.
4. Виділення повного квадрата.
5. Множення на сполучене вираження.
6. Однорідні ірраціональні рівняння.
7. Розкладання на множники.
8. Рівняння з кубічними ірраціональностями.
9. Заміна радикалів новими невідомими.
10. Уведення параметра.
11. Рівняння з модулями.
12. Системи ірраціональних рівнянь.
Ірраціональні рівняння
Рівняння називається ірраціональним, якщо невідоме входить під знак радикала або невідоме зводиться в ступінь із дробовим показником. Рішення ірраціонального рівняння зводиться до звільнення від ірраціональності і рішенню отриманого рівняння. При зведенні рівняння в ступінь можуть з'явитися сторонні корені. Тому необхідно робити перевірку, чи є знайдені корені рішеннями вихідного рівняння. Основним методом рішення ірраціональних рівнянь є зведення обох частин рівняння в ступінь. Приведемо основні способи рішення ірраціональних рівнянь.
1. Рівняння на одз
Знаходимо
ОДЗ з умов того, що підкореневе вираження
вираження
задовольняє умові
.
При рішенні ірраціонального рівняння
перевіряємо, чи входять знайдені корені
в ОДЗ.
Приклад. Розв’язати рівняння
.
Зведемо обидві частини рівняння в квадрат
.
Корінь
не задовольняє рівнянню, тому що під
коренем будуть негативні вираження.
Приклад. Розв’язати ірраціональне рівняння
.
Корені
,
не входять в ОДЗ
і не задовольняють рівнянню.
Приклад. Розв’язати рівняння
.
З рівнянь
знаходимо корені
,
,
.
Корінь
не входить в ОДЗ
і є стороннім.
Приклад. Розв’язати рівняння
.
Рівняння
має очевидний корінь
,
що не входить в ОДЗ і є стороннім. Після
скорочення на
одержимо рівняння
,
,
.
Варто оцінити значення лівої і правої частин рівняння в ОДЗ. Якщо вони не можуть бути рівними в ОДЗ, то рівняння не має рішення.
Приклад. Розв’язати рівняння
.
Знаходимо
ОДЗ
.
В ОДЗ виконана нерівність
,
.
Тому рівняння не має рішення.
Приклад. Розв’язати рівняння
.
Знаходимо ОДЗ із нерівностей
Рівняння рішень не має.
Приклад. Розв’язати рівняння
.
Знаходимо
ОДЗ:
.
В ОДЗ права частина рівняння негативна,
а ліва частина ненегативна. Рівняння
не має рішення,
.
2. Зведення рівняння в квадрат
Приклад. Розв’язати рівняння
.
Зведемо рівняння в квадрат
.
Приклад. Розв’язати рівняння
.
Праву та ліву частини рівняння возведемо в квадрат
Після приведення подібних членів одержимо
.
Приклад. Розв’язати рівняння
.
Перетворимо рівняння
.
Праву та ліву частини рівняння возведемо в квадрат
.
Це рішення не задовольняє рівнянню .
Приклад. Розв’язати рівняння
.
Праву та ліву частини рівняння возведемо в квадрат.
Одержимо:
Зведемо рівняння в квадрат
.
Рішення
,
не задовольняють рівнянню.
Приклад. Розв’язати рівняння
.
Праву та ліву частини рівняння возведемо в квадрат:
,
чи
.
3. Метод заміни
Заміна підкореневого вираза спрощує зведення ірраціонального рівняння до раціонального.
Приклад. Розв’язати рівняння
.
Позначимо
.
Одержимо рівняння :
Одержимо рівняння:
.
Приклад. Розв’язати рівняння
.
Позначимо
.
Одержимо рівняння:
.
Приклад. Розв’язати рівняння
.
Позначаючи
,
одержимо рівняння
.
.
Розв’яжемо рівняння
;
.
Приклад. Розв’язати рівняння
.
Позначаючи
.
Одержимо рівняння:
.
З рівняння
.
Приклад. Розв’язати рівняння
.
Позначаючи
.
Розв’яжемо
рівняння:
.
Звідси
знаходимо
.
Приклад. Розв’язати рівняння
.
Позначаючи
.
Одержимо рівняння:
.
Приклад .Розв’язати рівняння
.
Виділимо повний квадрат
.
Введемо
заміну:
.
З рівняння
,
знаходимо
.
.
Приклад. Розв’язати рівняння
.
Введемо
позначення
.
Рівняння прийме вид
.
Рівняння
рішення не має.
Рівняння
має корені:
.
Приклад. Розв’язати рівняння
.
Позначимо
.
Одержимо рівняння
.
Розв’яжемо рівняння
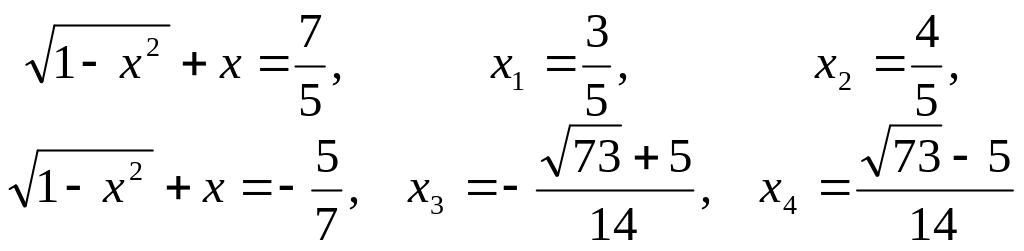
Корінь
— сторонній.
Приклад. Розв’язати рівняння
.
Позначимо
,
одержимо рівняння
.
. Знаходимо
.